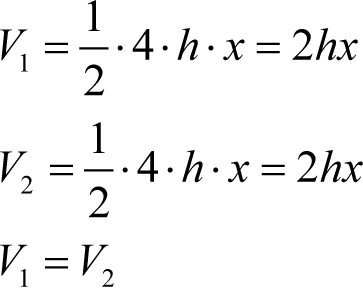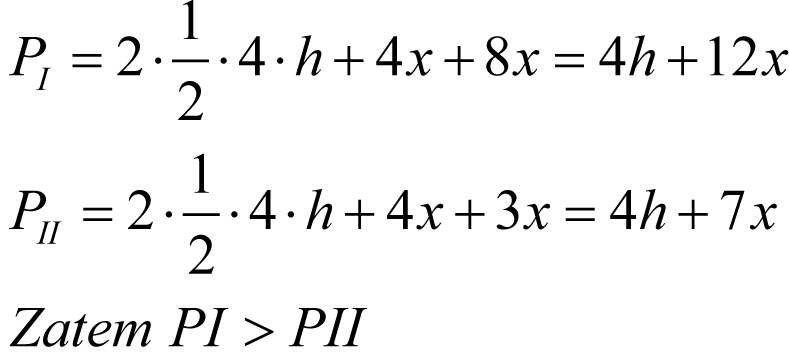Graniastosłup
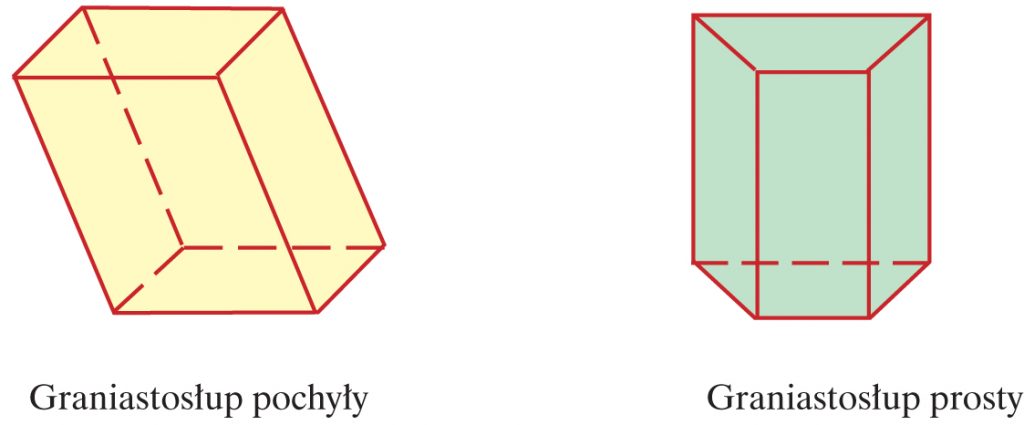
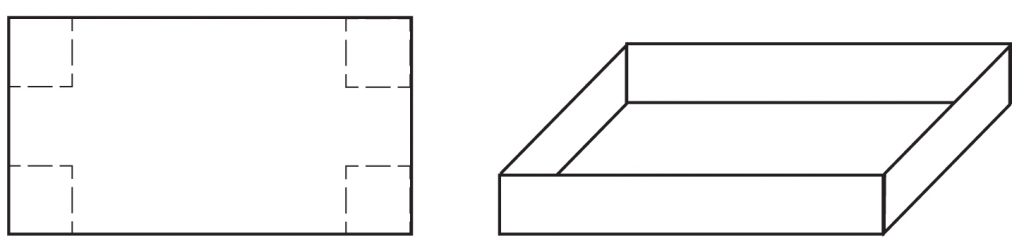
Graniastosłupem nazywamy figurę przestrzenną, której dwie ściany zwane podstawami są przystającymi wielokątami zawartymi w płaszczyznach równoległych, a ściany boczne są równoległobokami.
W graniastosłupie prostym wszystkie ściany boczne są prostokątami oraz są prostopadłe do podstawy. Graniastosłupem prostym czworokątnym jest m. in. prostopadłościan.
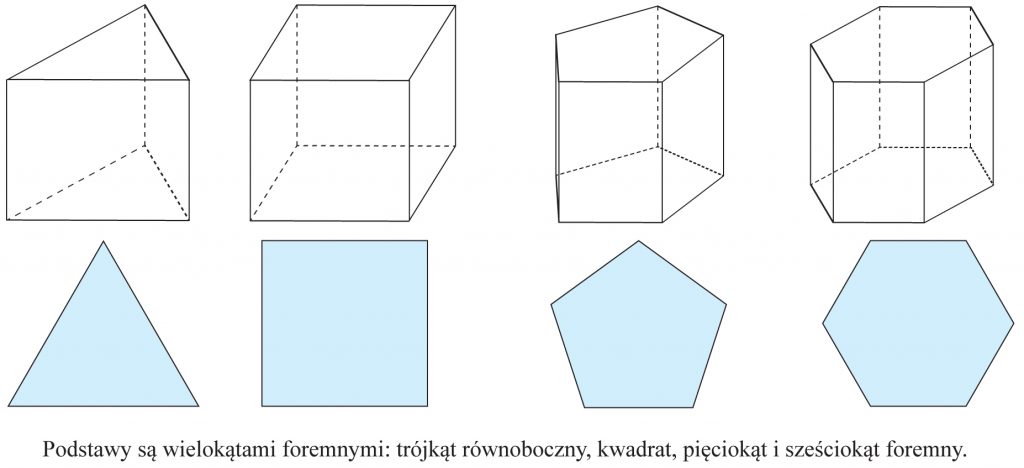
Graniastosłup prawidłowy (bądź graniastosłup foremny) – to taki graniastosłup prosty, którego każda podstawa jest jakimkolwiek wielokątem foremnym (tj. mającym równe boki oraz takie same kąty). Wielokątami foremnymi są np.: trójkąt równoboczny, kwadrat, sześciokąt foremny.
Zapamiętaj!
- Wysokość graniastosłupa to odcinek prostopadły do podstaw, którego końce leżą na płaszczyznach, w których się te podstawy zawierają.
- Pole powierzchni graniastosłupa jest to suma pól wszystkich ścian bocznych i dwóch podstaw (jest ono równe polu powierzchni jego siatki).
Pc = 2Pp + Pb
Pc – pole powierzchni całkowitej
Pp – pole powierzchni podstawy
Pb – suma pól ścian bocznych
Zauważ!
- Obliczając pola powierzchni i objętości prostopadłościanów, należy pamiętać, że długości wszystkich krawędzi muszą być wyrażone w tej samej jednostce.
- Ze względów praktycznych pojęcie objętości zastępujemy niekiedy przez pojęcie pojemności wyrażające objętość dowolnej substancji mieszczącej się w ustalonym naczyniu.
Zadanie 1
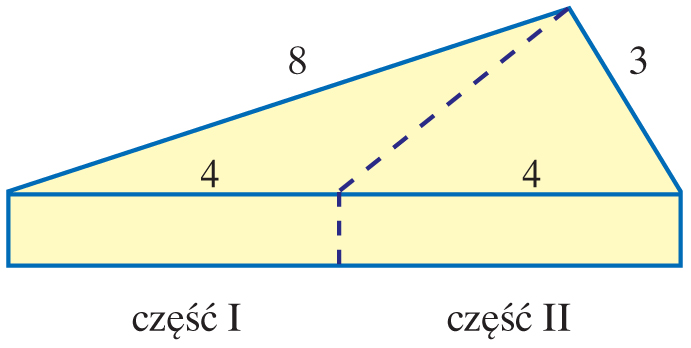
Serek ma kształt graniastosłupa, którego podstawą jest trójkąt o długościach boków:
8 cm, 8 cm i 3 cm. Wojtek i Ewa postanowili podzielić serek na dwie części o równych objętościach. Wojtek lubi skórkę pokrywającą całą powierzchnię serka, więc zaprojektował cięcie jak na rysunku. Czy rzeczywiście obie części mają tę samą objętość? Która część ma większą powierzchnię skórki? Odpowiedź uzasadnij.
Rozwiązanie:
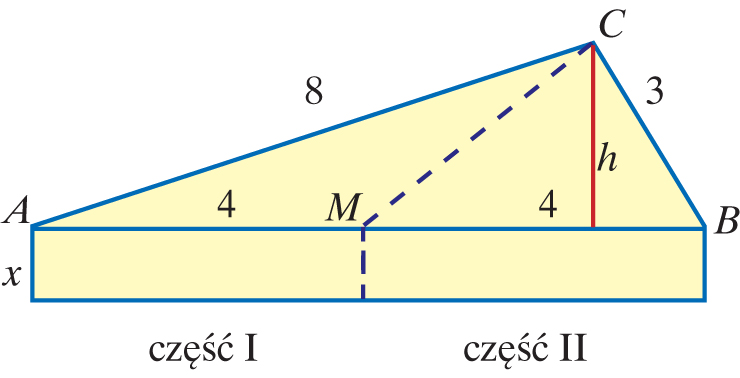
Niech x oznacza wysokość graniastosłupa (serka), a h wysokość trójkąta AMC i MBC. Stąd:
Dalej można zauważyć, że pola powierzchni ze skórką wynoszą:
Odpowiedź: Obie części mają tę samą objętość, a większą powierzchnię ze skórką ma część I.
Zadanie 2
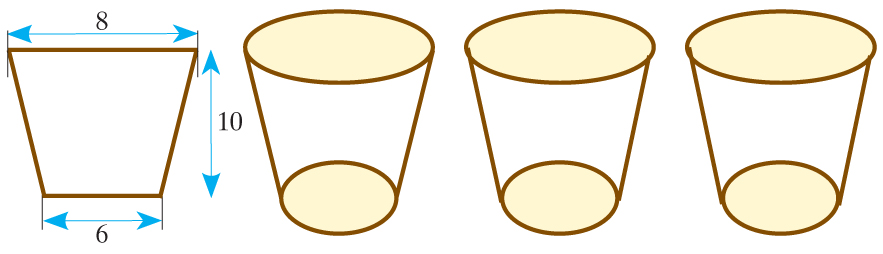
Masz kubki o wymiarach zewnętrznych: wysokość 10 cm, średnica dolna 6 cm, średnica górna 8 cm.
Zaprojektuj otwarte, prostopadłościenne pudełko (bez przykrycia) tak, aby zmieścić w nim trzy kubki. Przy pakowaniu nie można wkładać kubka w kubek. (Wskazówka : najpierw ustal możliwie najmniejsze wymiary pudełka (odpowiednio ustawiając kubki) i wpisz je na modelu.) Następnie narysuj siatkę pudełka w skali 1:4 i podaj wymiary siatki w skali.
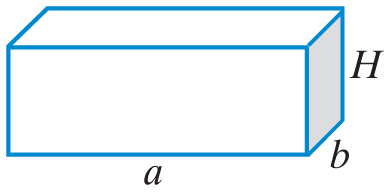
Oblicz, ile cm² papieru trzeba zużyć na wyklejenie wnętrza zaprojektowanego pudełka.
Rozwiązanie:
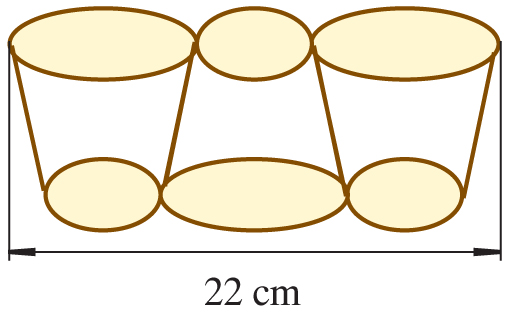
Przykładowe ustawienie kubków w pudełku
– takie ustawienie daje najmniejsze wymiary pudełka:
Wymiary pudełka: a = 22 cm, b = 8 cm, H = 10 cm
Kształt siatki:
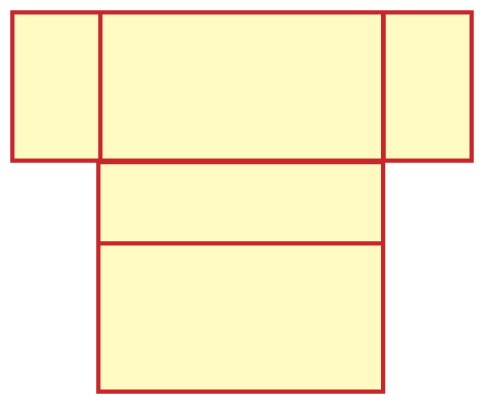
Wymiary siatki w skali 1:4: a1 = 5,5 cm, b1 = 2 cm, H1 = 2,5 cm.
Obliczymy teraz, ile cm² papieru trzeba zużyć na wyklejenie wnętrza zaprojektowanego pudełka:
Pc = Pp + Pb = ab + 2(aH + bH)
Pc = 22 × 8 + 2 × (22 × 10 + 8 × 10) = 176 + 600 = 776 [cm²].
Odpowiedź: Na wyklejenie wnętrza zaprojektowanego pudełka potrzeba 776 cm2 papieru.
Zadanie 3
Akwarium, w którym Marek hoduje rybki, ma wymiary 5 dm, 8 dm, 6 dm. Marek wlewa do pustego akwarium wodę przepływającą przez kran z szybkością 8 dm³ na minutę. Do jakiej wysokości woda w akwarium będzie sięgać po 10 min? Zapisz obliczenia.
Rozwiązanie:
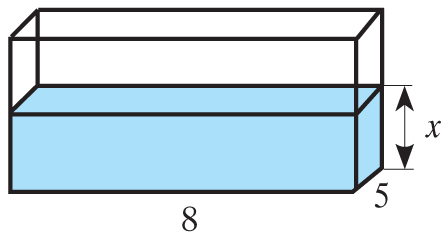
x – wysokość wody w akwarium
Skoro w ciągu jednej minuty do akwarium wlewa się 8 dm³ wody, to w ciągu 10 minut wleje się 80 dm³ wody (8 × 10 = 80).
Objętość wody znajdującej się w akwarium można zapisać według wzoru V = 5 × 8 × x. Stąd otrzymujemy równanie:
5 × 8 × x = 80
x = 2 [dm]
Uwaga! Zwróć uwagę na to, że w obliczeniach nie wykorzystujemy wcale tego, że wysokość akwarium wynosi 6 dm.
Odpowiedź: Po 10 min woda będzie sięgała do wysokości 2 dm.
Zadanie 4
Podczas mroźnej zimy uczniowie planowali urządzić lodowisko na boisku szkolnym. Będzie miało ono kształt prostokąta o wymiarach 24 m i 33 m. Na każdy metr kwadratowy boiska uczniowie planowali wylać 40 litrów wody. Woda miała być dowożona cysterną o pojemności 5000 litrów. Ile co najmniej razy musiałaby przyjeżdżać cysterna, aby przywieźć całą potrzebną wodę? Zapisz obliczenia.
Rozwiązanie:
Najpierw obliczymy pole powierzchni boiska oraz objętość wody, która ma być wylana:
P = 24 m · 33 m = 792 m²
Vw = 792 · 40 = 31 680 [litrów]
Ponieważ jedna cysterna ma pojemność 5000 l, więc musiałaby przyjeżdżać co najmniej
7 razy (31 680 : 5000 = 6,336).
Zadanie 5
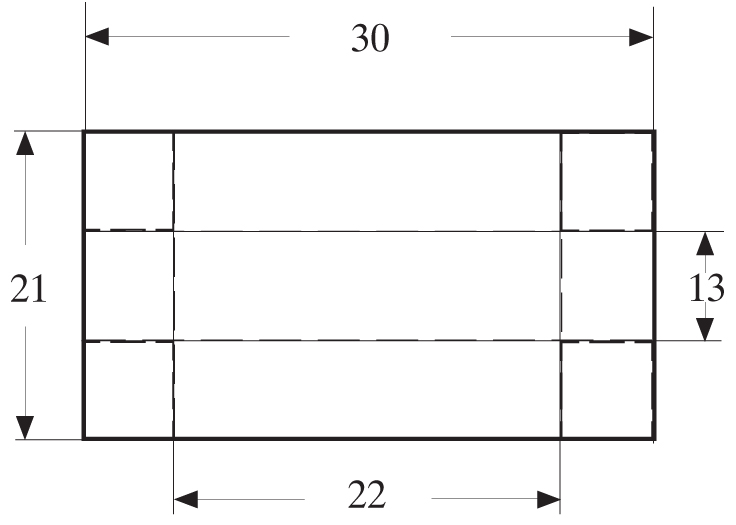
Z prostokątnego arkusza tektury o wymiarach 21 cm x 30 cm wycięto w rogach równe kwadraty o boku 4 cm i zgięto brzegi arkusza do góry, tworząc otwarte pudełko. Ile co najwyżej klocków sześciennych o boku 2 cm zmieści się w tym pudełku?
Powtórz!
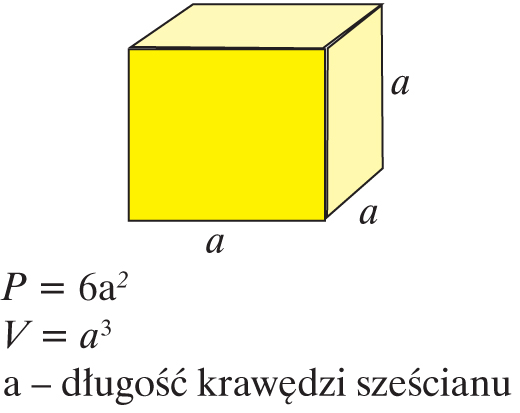
Sześcian to prostopadłościan, którego każda ściana jest kwadratem. Pole powierzchni sześcianu jest równe sumie pól sześciu kwadratów. Objętość sześcianu jest równa iloczynowi trzech krawędzi wychodzących z jednego wierzchołka.
Rozwiązanie:
Obliczamy wymiary dna pudełka:
30 – 2 · 4 = 22
21 – 2 · 4 = 13
Teraz ustalimy, ile kostek sześciennych o boku 2 cm zmieści się w jednej warstwie: wzdłuż krawędzi o długości 22 cm ustawimy 11 klocków (22 : 2 = 11), a wzdłuż krawędzi o długości 13 cm 6 klocków (13 : 2 = 6,5). Z tego wynika, że w jednej warstwie umieścimy 66 klocków (11 · 6 = 66). Ponieważ wysokość pudełka wynosi 4 cm, więc ułożymy w nim dwie warstwy kostek sześciennych, czyli 132 klocki (66 · 2 = 132).
Odpowiedź: W pudełku zmieszczą się co najwyżej 132 klocki.
Poćwicz
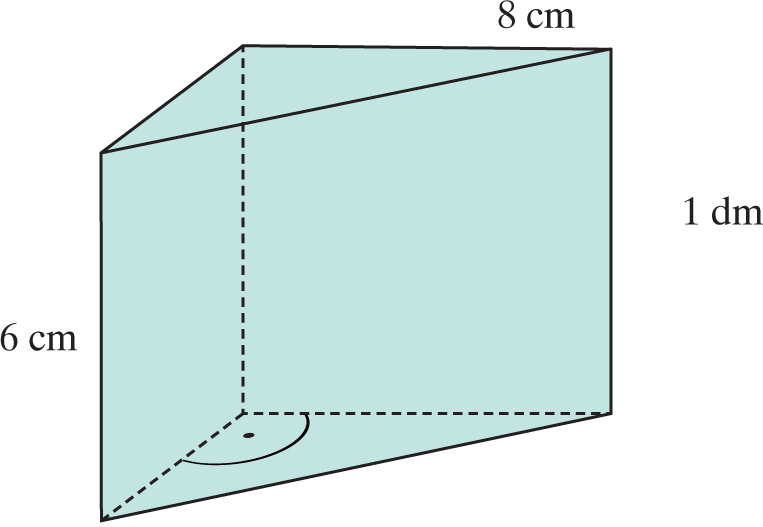
1. Ile cm² papieru potrzeba do oklejenia pudełka w kształcie graniastosłupa, którego rzut przedstawia rysunek:
A. 240 cm²
B. 288 cm²
C. 480 cm²
D. 100 cm²
2. Podstawa graniastosłupa prawidłowego jest kwadratem o boku długości 5 j. Pole powierzchni całkowitej jest równe 210 j2. Którym z równań obliczysz wysokość tego graniastosłupa?
A. 2 × 52 + 4 × 5 × h = 210
B. 52 + 4 × 5 × h = 210
C. 4 × 5 × h = 210
D. 2 × 5 + 2 × 5 × h = 210
Odpowiedzi:
1. B, 2. A