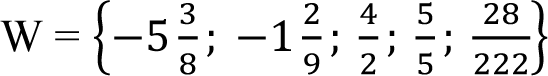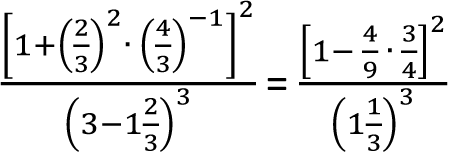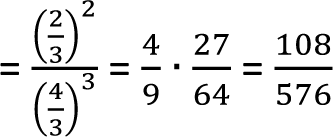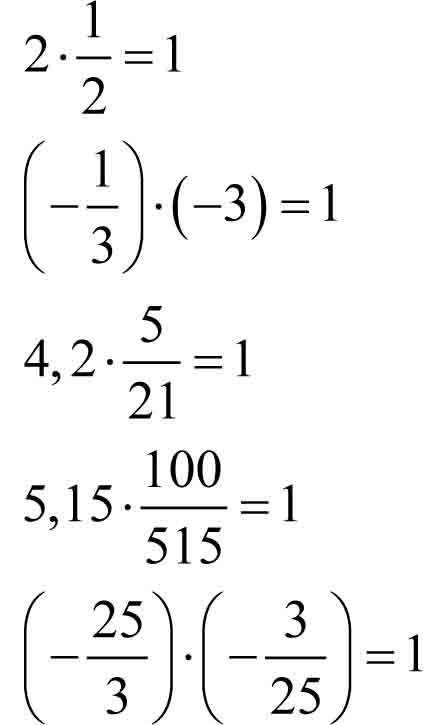Liczby naturalne

Najważniejszym zbiorem liczbowym, który poznała ludzkość, jest zbiór liczb naturalnych N Liczby naturalne to liczby używane powszechnie do liczenia i ustalania kolejności.
Zbiór liczb naturalnych N zawiera w sobie następujące elementy

N = {1, 2, 3, 4, …} lub N = {0, 1, 2, 3, 4, …}.

Uwaga! Nie ma zgodności matematyków co do przynależności zera do liczb naturalnych. Zatem korzystać z niego będziemy zgodnie z potrzebą.

Liczby naturalne zapisujemy za pomocą znaków zwanych cyframi 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 i za ich pomocą można zapisać każdą liczbę naturalną.

 

Liczby całkowite

Zbiór liczb całkowitych C zawiera w sobie

  • zbiór liczb naturalnych,
  • zbiór liczb przeciwnych do naturalnych
  • liczbę 0.

C = {… -4, -3, -2, -1, 0, 1, 2, 3, 4, …}.

Liczby wymierne

Liczba wymierna – to taka liczba, którą można zapisać w postaci ilorazu dwóch liczb całkowitych, gdzie druga jest różna od zera. Zatem zbiór liczb wymiernych to po prostu ułamki. Każdą liczbę całkowitą można zapisać w postaci ułamka (zero również), zatem każda liczba całkowita jest liczbą wymierną.

liczby wymierne 22

Liczby niewymierne

Liczby, które nie dadzą zapisać się w postaci ułamków nazywamy liczbami niewymiernymi.
Przykłady liczb niewymiernych to:

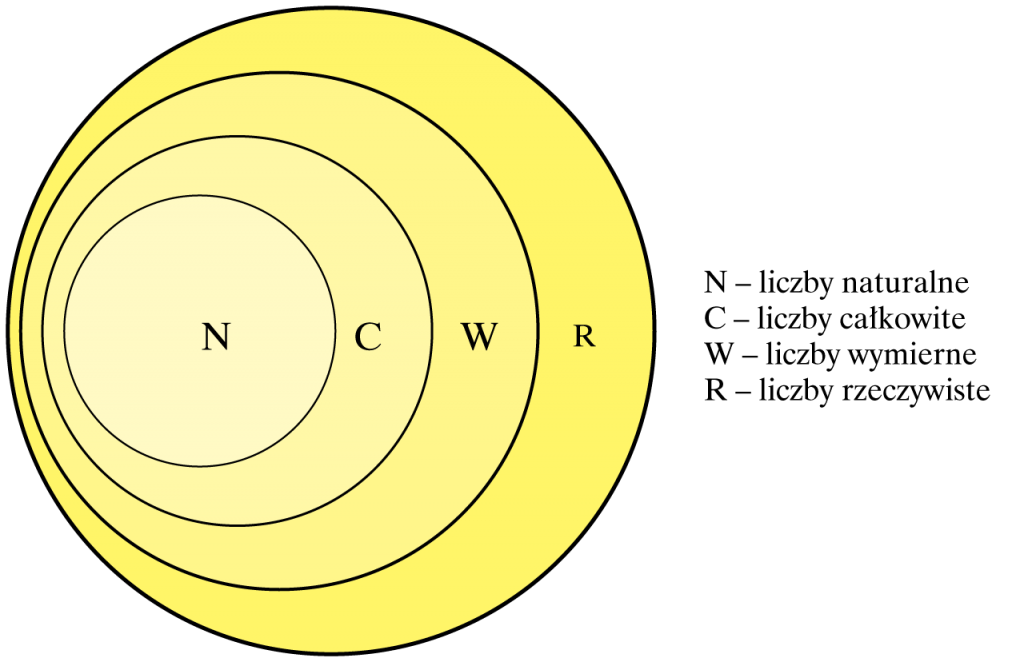
liczby niewymierne

Liczby rzeczywiste

Zbiór liczb wymiernych i zbiór liczb niewymiernych tworzą razem zbiór liczb rzeczywistych R.
Zależności wymienionych zbiorów ilustruje rysunek:

Liczby

Uwaga
Mówimy, że działanie jest wykonalne w danym zbiorze, jeżeli wynik tego działania na liczbach należących do danego zbioru jest liczbą również należącą do danego zbioru.

Prawa ułatwiające wykonywanie działań

1. przemienność dodawania i mnożenia

a + b = b + a
a · b = b · a

2. łączność dodawania i mnożenia

(a + b) + c = a + (b + c)
(a · b) · c = a · (b · c)

3. rozdzielność mnożenia i dzielenia względem dodawania lub odejmowania

a · (b ± c) = a · b ± a · c
(a ± b) : c = a : c ± b : c

Liczby neutralne

Czy istnieje taka liczba w konkretnym działaniu, która nie ma wpływu na wynik tego działania? Ależ tak.

  • W dodawaniu to zadanie spełnia liczba 0 a w mnożeniu liczba 1.
  • Mówimy, że „0” jest elementem neutralnym dodawania, a „1” jest elementem neutralnym mnożenia.

Liczby „0” i „1” nadają ciekawe właściwości poszczególnym działaniom:

a + 0 = a a · 1 = a
a – 0 = a a : 1 = a
a – a = 0 a : a = 1
a · 0 = 0
0 : a = 0
a : 0 – działanie niewykonalne

Działania odwrotne

Działania: dodawanie i odejmowanie oraz mnożenie i dzielenie są odwrotnymi względem siebie tzn., że

  • jeżeli a + b = c, to a = c – b b = c – a
  • jeżeli a – b = c, to a = b + c b = c – a
  • jeżeli a : b = c, to a = b · c b = c : a gdy a ≠ 0 i b ≠ 0
  • jeżeli a · b = c, to a = c : b b = c : a gdy a ≠ 0 i b ≠ 0

Kolejność wykonywania działań

Zbiór liczb rzeczywistych R jest zbiorem, w którym wymienione wyżej działania są wykonalne. Jeśli występuje w pewnym wyrażeniu więcej działań niż jedno, to ich kolejność wykonywania reguluje umowa, która głosi:

1. Gdy występują tylko działania odwrotne do siebie (tzn. dodawanie i odejmowanie lub mnożenie i dzielenie) to wykonujemy je w kolejności w jakiej są zapisane np.:

a) -12 + 11 – 8 + 39 = – 1 – 8 + 39 = – 9 + 39 = 30
b) 48 : (-8) · 3 : 9 = (-6) · 3 : 9 = (-18) : 9 = -2

2. Gdy w wyrażeniu występują cztery działania bez nawiasów, to wykonujemy najpierw mnożenie, dzielenie a potem dodawanie i odejmowanie np.:

2 · (-24) – 340 : (-17) – (-2) · (-12) = -48 + 20 – 24 = -28 – 24 = – 52
. 1 2 3 1 2 3
lub w końcowej fazie inaczej = – 48 + 20 – 24 = – 72 + 20 = -52

3. Gdy w wyrażeniu występują nawisy, to najpierw wykonujemy działania w nawiasach, a potem tak jak w punkcie 2, np.:

(-2) · (-1 + 7) – 1 = ( -2) · 6 – 1 = -12 – 1 = -13

4. Jeśli w wyrażeniu występuje potęgowanie lub pierwiastkowanie, to te działania mają pierwszeństwo, np.:

1 22

1 222

Obliczanie wartości wyrażeń można przedstawić za pomocą grafu np.: wyrażenie

można zapisać i obliczyć jego wartość przy pomocy drzewka:

27 22
Rozwiązanie dzielimy na etapy:

a) 3 22
b) 2 · 4 = 8
c) (-16) : 8 = -2

Rozwiązywanie bez drzewka:

= 5 222

Wartość bezwzględna i liczby przeciwne

Liczby mające taką samą wartość bezwzględną, ale różne znaki, nazywamy liczbami przeciwnymi, np.:

5 i –5; 4 i –4; –1 i 1;

Uwaga!

  • Zero jest liczbą przeciwną do siebie samej.
  • Liczby przeciwne leżą na osi liczbowej po obu stronach zera w jednakowej odległości od zera.
  • Suma liczb przeciwnych jest równa zeru.
    5 + (-5) = 0
    (–1) + 1 =0
    2,75 + (–2,75) = 0


Odwrotność liczby

Odwrotność liczby to iloraz liczby 1 przez daną liczbę.

Iloczyn liczby danej przez jej odwrotność równy jest jeden, np.:

 

Podzielność liczb

Mówimy, że liczba a jest podzielna przez liczbę b wtedy, gdy reszta z tego dzielenia równa jest zeru

  • liczbę a nazywamy wielokrotnością liczby b
  • liczbę b nazywamy podzielnikiem liczby a

Odwrotność liczby potrzebna jest przy dzieleniu ułamków.

Uwaga: liczba 0 nie ma odwrotności, gdyż dzielnikiem nie może być zero.

Liczby pierwsze
Liczbą pierwszą nazywamy taką liczbę, która ma dokładnie dwa podzielniki – liczbę 1 i samą siebie, np..: 2, 3, 5, 7, 11, 13, …

Liczby złożone
Liczbą złożoną nazywamy taką liczbę, która ma więcej niż dwa podzielniki, np.
4 (dzieli się przez 1, 2, 4) , 6 (dzieli się przez 1, 2, 3, 6) , 8, 9, 10, 12, 14, …

Uwaga! Liczba 1 nie jest ani liczbą pierwszą ani złożoną.

Liczba a Podzielniki liczby a Wielokrotności liczby a

2 1, 2 2, 4, 6, 8, …
3 1, 3 3, 6, 9, 12, …
4 1, 2, 4 4, 8, 12, 16, …
8 1, 2, 4, 8 8, 16, 24, 32, …

Liczby podzielne przez 2 nazywamy liczbami parzystymi.
Liczby, które nie są podzielne przez 2 nazywamy liczbami nieparzystymi.

  • Liczby podzielne przez 2 nazywamy wielokrotnościami liczby 2.
  • Liczby podzielne przez 3 nazywamy wielokrotnościami liczby 3.
  • Liczby podzielne przez 4 nazywamy wielokrotnościami liczby 4 itd.

Jak rozpoznać czy dana liczba jest podzielna przez inną liczbę?

Do tego służą cechy podzielności liczb przez 2, 3, 4, 5, 10, 25, 100 itd.

  • Liczba jest podzielna przez 2 wtedy, gdy ostatnia cyfra tej liczby jest podzielna przez 2 tzn.: 2, 4, 6, 8.
  • Liczba jest podzielna przez 5 wtedy, gdy ostatnia cyfra tej liczby jest 0 lub 5.
  • Liczba jest podzielna przez 4 wtedy, gdy ostatnie dwie cyfry tej liczby tworzą liczbę podzielną przez 4 np.:
    • 512 (12 jest podzielne przez 4),
    • 1 616 (16 jest podzielne przez 4),
    • 55 120 (16 jest podzielne przez 4).
  • Liczba jest podzielna przez 25 wtedy, gdy ostatnie dwie cyfry tej liczby tworzą liczbę podzielną przez 25 tzn.: 00; 25; 50; 75;
    • 200
    • 1925
    • 11 575
  • Liczba jest podzielna przez 10, wtedy, gdy ostatnia jej cyfra wynosi 0.
  • Liczba jest podzielna przez 100 wtedy, gdy dwie ostanie jej cyfry są zerami.
  • Liczba jest podzielna przez 3 wtedy, gdy suma jej cyfr jest podzielna przez 3.
  • Liczba jest podzielna przez 9 wtedy, gdy suma jej cyfr jest podzielna przez 9.
    • 666 (6+6+6=18 – 18 jest podzielne przez 3)
    • 711 (7+1+1=9 – 9 jest podzielne przez 3)
  • Jeżeli liczba jest podzielna przez 2 i 3 równocześnie to jest również podzielna przez 6.
  • Jeżeli liczba jest podzielna przez 3 i 5 równocześnie to jest również podzielna przez 15.

Największy wspólny podzielnik

Największym wspólnym podzielnikiem (NWD) dwóch lub więcej liczb jest największa liczba naturalna, przez którą podzielna jest każda z tych liczb.

Jeśli szukamy największego wspólnego podzielnika dwóch liczb np.: 24, 36 obie liczby należy rozłożyć na czynniki pierwsze wyszukując tylko wspólne podzielniki tych liczb.

1. Obie liczby 24 i 36 dzielą się przez 2 (jest to wspólny podzielnik)
24 2 36 2

2. Po podzieleniu otrzymujemy liczby 12 i 18, które obie dzielą się przez 2
12 2 18 2

3. Po podzieleniu otrzymujemy liczby 6 i 9, które obie dzielą się przez 3

6 3 9 3
2 3

4. Teraz mnożymy wspólne podzielniki NWP (24, 36) = 2 · 2 · 3 = 12

Uwaga! Odszukiwanie NWP (Największego wspólnego podzielnika) jest potrzebne przy skracaniu ułamków.

Najmniejsza Wspólna Wielokrotność

Najmniejszą wspólna wielokrotność (NWW) to najmniejsza liczba naturalna, podzielna przez każdą z tych liczb.

Jak znaleźć NWW liczb 24 i 36?

Można tak:

1. Rozkładamy obie liczby na czynniki pierwsze.

2. W rozkładzie drugiej liczby wykreślamy (o ile istnieją) wspólne czynniki. Iloczyn wszystkich nieskreślonych czynników obu liczb jest najmniejszą wspólną wielokrotnością tych liczb.

24 2 36 2 (liczbę 2 wykreślamy, bo się powtarza)
12 3 18 3 (liczbę 3 wykreślamy, bo się powtarza)
4 2 6 2 (liczbę 2 wykreślamy, bo się powtarza)
2 2 3 3
1 1
Najmniejszą wspólną wielokrotnością liczb 24 i 36 jest liczba 72 = 2 • 3 • 2 • 2 • 3

Uwaga!
Odszukiwanie NWW potrzebne jest przy sprowadzaniu ułamków do wspólnego mianownika.

Zobacz:

Zbiory i przedziały liczbowe