Tag "geometria"
Zadania na klasówkę! Zadanie 1. Działka jest prostokątem o wymiarach 80 m i 900 dm. Wyraź w arach powierzchnię tej działki. Rozwiązanie: Ponieważ 1 a = 100 m², więc obliczenia najwygodniej prowadzić w metrach. Wymiary działki: a = 80 m, b = 900 dm = 90 m. Stąd P = 80 m ⋅ 90 m = 7200 m² = 72 a Odpowiedź: Powierzchnia działki wynosi 72 ary. Zadanie 2. Podłoga
Prosta, płaszczyzna, punkt, odcinek, łamana, kąt, rodzaje kątów W geometrii istnieją pojęcia PIERWOTNE, których definicji nie jesteśmy w stanie podać. Do takich pojęć należy: PUNKT, PROSTA, PŁASZCZYZNA.Wszystkie inne pojęcia są pochodnymi pierwotnych i dzięki nim definiowane. PUNKT oznaczamy dużymi literami alfabetu, np.: • A • B • C PROSTE oznaczamy małymi literami alfabetu np. : p Prosta jest to linia, która nie ma ani początku ani końca. Punkt leżący
Okręgiem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O wynosi r. Kołem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O jest mniejsza lub równa r. Zauważ! Środek okręgu nie należy do okręgu, środek koła należy do koła. To jest ważne! W okręgu i kole można zaznaczyć: Promień r – odcinek, którego jednym końcem jest środek okręgu O, a drugi koniec leży na okręgu. Cięciwę c – odcinek,
H – wysokość bryły Pp – pole podstawy Pb – pole powierzchni bocznej V – objętość bryły P – pole powierzchni bryły Graniastosłup Sześcian Prostopadłościan Ostrosłup Walec Stożek ścięty Kula
Graniastosłup Graniastosłupem nazywamy figurę przestrzenną, której dwie ściany zwane podstawami są przystającymi wielokątami zawartymi w płaszczyznach równoległych, a ściany boczne są równoległobokami. Uwaga! W graniastosłupie prostym ściany boczne są prostokątami (są prostopadłe do podstaw). Zapamiętaj! Graniastosłup nazywamy prawidłowym, jeśli jest prosty i podstawy są wielokątami foremnymi. Wielokątami foremnymi są np. trójkąt równoboczny, kwadrat, sześciokąt foremny. Przekątna graniastosłupa – to odcinek łączący dwa wierzchołki nienależące do płaszczyzny jednej ściany. Uwaga! Graniastosłup trójkątny ma
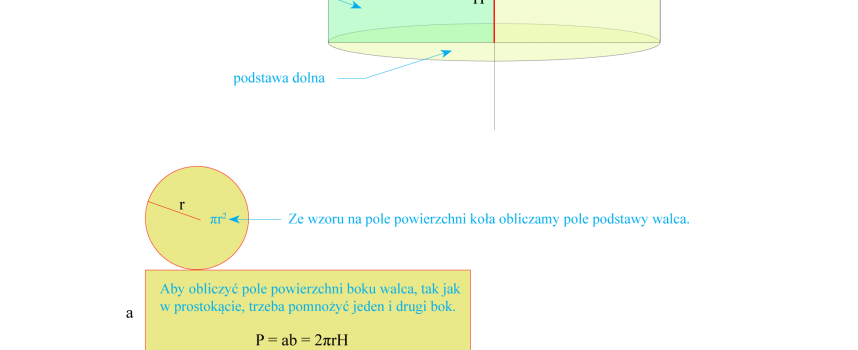
Walec Walec jest figurą przestrzenna, która powstaje przez obrót prostokąta wzdłuż prostej zawierającej jeden z jego boków. Pole powierzchni całkowitej walca to suma pól podstaw dolnej i górnej (dwa koła) i powierzchni bocznej, która jest prostokątem o długości równej długości okręgu podstawy i szerokości równej wysokości walca) Pc = 2 · Pp + Pb Pc = 2πr2 + 2πrH r – długość promienia koła H – wysokość walca Objętość walca (mnożymy
Narysujmy na płaszczyźnie dwie różne półproste o wspólnym początku, nie należące do jednej prostej. Płaszczyzna została podzielona w ten sposób na dwa obszary, z których każdy nazywamy kątem. Wspólny początek półprostych nazywamy wierzchołkiem kąta, a owe półproste – jego ramionami. Oznaczenia kątów: trzyliterowe : ramię, wierzchołek, ramię oznaczają wnętrze kąt jednoliterowe – greckie litery α, β, γ, δ Rodzaje kątów Przy rozwiązywaniu zadań potrzebna też będzie znajomość kątów: Zadania Rysunek
Walec Walec jest figurą przestrzenną, która powstaje przez obrót prostokąta wzdłuż jednego z jego boków. Pole powierzchni całkowitej walca to suma pól podstaw (dolnej i górnej) i powierzchni bocznej Pc = 2 · Pp + Pb r – długość promienia koła H – wysokość walca Objętość walca r – długość promienia podstawy walca H – wysokość walca Stożek Stożek jest to figura przestrzenna powstała przez obrót trójkąta prostokątnego wzdłuż jednej
Zapamiętaj Przestrzeń jest pojęciem pierwotnym, którego nie definiujemy. Przestrzeń składa się z punktów i jest nieograniczona w żadnym kierunku. Płaszczyzna Jest to jedno z pierwotnych pojęć geometrii. Możemy wyobrazić ją sobie jako powierzchnię płaską, nieskończenie wielką, nieposiadającą brzegów ani końca. Płaszczyzny najczęściej oznaczamy małymi literami alfabetu greckiego: α, β, γ. η itd. Prosta i płaszczyzna Jakie może być wzajemne położenie prostej i płaszczyzny w przestrzeni? Prosta może przecinać płaszczyznę i ma
Okrąg Okręgiem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O wynosi r. Okręg oznaczamy o (O,r) i czytamy okrąg o środku w punkcie O i promieniu r. Promień okręgu jest to odcinek łączący środek okręgu z dowolnym punktem okręgu. Cięciwa jest to odcinek łączący dwa dowolne punkty okręgu. Średnica jest to cięciwa przechodząca przez środek okręgu. Styczna jest to prosta mająca z okręgiem tylko jeden punkt wspólny. Kąt
Czworokąt jest to część płaszczyzny ograniczona łamaną zwyczajną zamkniętą złożoną z 4 odcinków. Ma cztery wierzchołki i cztery kąty wewnętrzne, których suma wynosi 360°. Łatwo można sprawdzić, że suma miar kątów wewnętrznych czworokąta wynosi 360°. Jeżeli w dowolnym czworokącie poprowadzisz jedną przekątną, to czworokąt zostanie podzielony na dwa trójkąty. Ponieważ suma miar kątów jednego trójkąta wynosi 180°, więc w obu jest ona równa 360°. Wierzchołki czworokąta oznaczamy dużymi literami alfabetu A, B, C,
POWTARZAMY TRÓJKĄTY Wielokątem o najmniejszej liczbie boków jest trójkąt. Trójkąt to część płaszczyzny ograniczona łamaną zwyczajną zamkniętą złożoną z 3 odcinków. Trójkąt ma trzy wierzchołki i trzy kąty wewnętrzne. A, B, C – wierzchołki trójkąta AB, AC, BC – boki trójkąta ABC, ACB, CAB – kąty wewnętrzne trójkąta Zapamiętaj! Wierzchołki trójkąta oznaczamy dużymi literami A, B, C. Boki trójkąta oznaczamy małymi litrami a, b, c. Kąty oznaczamy greckimi literami α (przy wierzchołku
WIELOKĄTY Zapamiętaj! Figury wypukłe – figury, w których każdy odcinek łączący dwa dowolne punkty tej figury jest zawarty w tej figurze. Figury niewypukłe – figury, w których można wskazać taki odcinek, którego końce należą do figury, ale odcinek nie zawiera się całkowicie w figurze. Co to jest wielokąt? Wielokątem nazywamy część płaszczyzny ograniczoną łamaną zwyczajną zamkniętą wraz z tą łamaną. Boki łamanej nazywamy bokami wielokąta, a jej wierzchołki – wierzchołkami wielokąta. Wierzchołek
W geometrii istnieją pojęcia pierwotne, których definicji nie jesteśmy w stanie podać. Do takich pojęć należy: PUNKT, PROSTA, PŁASZCZYZNA.Wszystkie inne pojęcia są pochodnymi pierwotnych i dzięki nim definiowane. Zapamiętaj! Punkt, prosta i płaszczyzna to pojęcia pierwotne, których nie definiujemy. Punkt Punkty oznaczamy dużymi literami alfabetu łacińskiego: A, B, C, M, N, K, L, P… Punkty zaznaczamy za pomocą kropek lub dwóch przecinających się kreseczek. A • × B