Zapamiętaj

  • Przestrzeń jest pojęciem pierwotnym, którego nie definiujemy.
  • Przestrzeń składa się z punktów i jest nieograniczona w żadnym kierunku.

Płaszczyzna

Jest to jedno z pierwotnych pojęć geometrii. Możemy wyobrazić ją sobie jako powierzchnię płaską, nieskończenie wielką, nieposiadającą brzegów ani końca.

  • Płaszczyzny najczęściej oznaczamy małymi literami alfabetu greckiego: α, β, γ. η itd.

 

Prosta i płaszczyzna

Jakie może być wzajemne położenie prostej i płaszczyzny w przestrzeni?

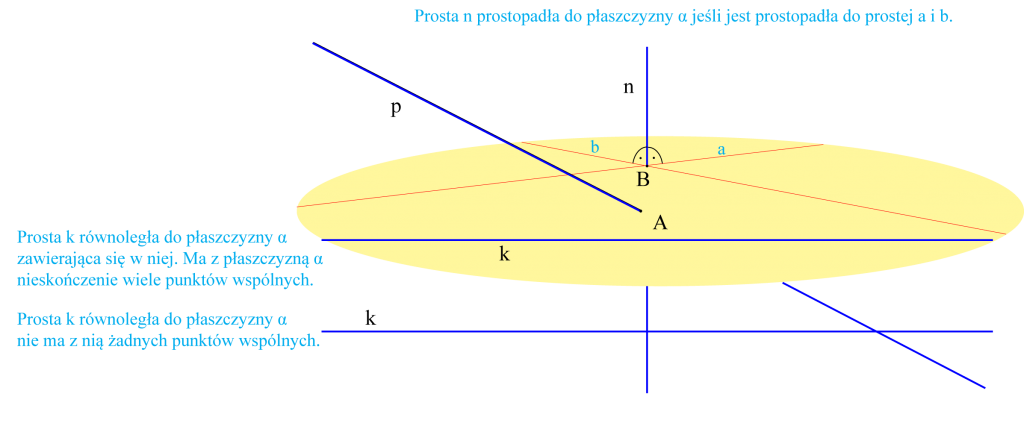
płaszczyzna i proste 22

  • Prosta może przecinać płaszczyznę i ma wówczas jeden punkt wspólny (A) z płaszczyzną (np. α).
    Wśród prostych przecinających płaszczyznę wyróżniamy proste prostopadłe do płaszczyzny.
    Prosta n przecinająca płaszczyznę α w punkcie B jest do tej płaszczyzny prostopadła, jeśli jest prostopadła do dwóch różnych prostych (np. a, b na rysunku) leżących na tej płaszczyźnie i przechodzących przez punkt B.
  • Prosta może być równoległa do płaszczyzny. Może nie mieć punktów wspólnych lub (jeśli zawiera się w tej płaszczyźnie) nieskończenie wiele.

Wzajemne położenie dwóch płaszczyzn

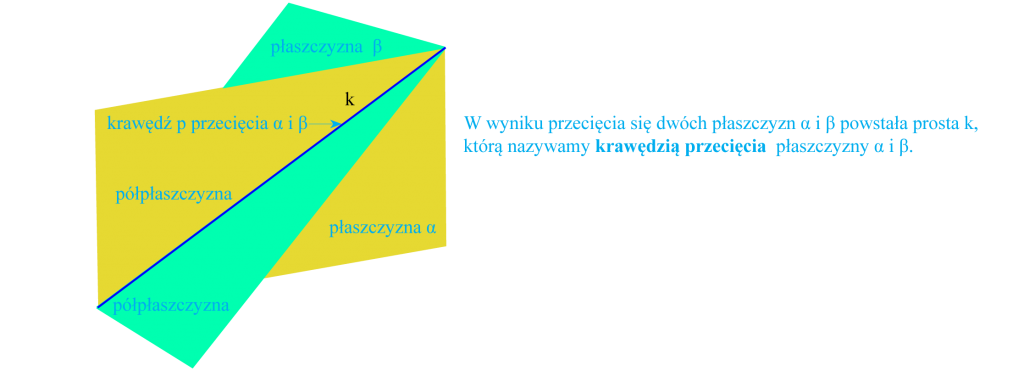
  • Dwie płaszczyzny w przestrzeni mogą się przecinać. Ich wspólne punkty tworzą prostą, która nazywa się krawędzią przecięcia się tych płaszczyzn.

przecięcie płaszczyzn 22

 

  • Dwie płaszczyzny w przestrzeni mogą być równoległe (nie mają wówczas żadnych punktów wspólnych) lub się pokrywać (mają wówczas nieskończenie wiele punktów wspólnych).

płaszczyzny równoległe 22

 

Kąt dwuścienny

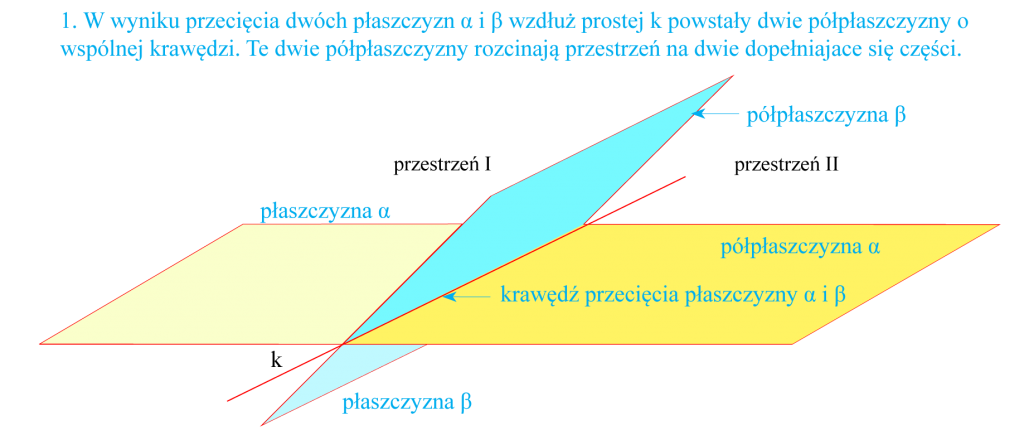
kąt dwuścienny 1

Kątem dwuściennym nazywamy każdą z dwóch części, na jakie rozcinają przestrzeń dwie półpłaszczyzny o wspólnej krawędzi wraz punktami każdej półpłaszczyzny.

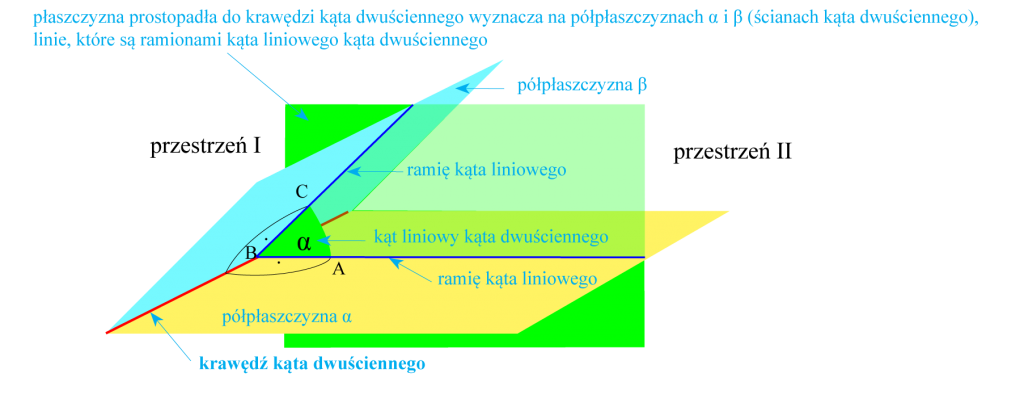
kąt dwuścienny 222

Półpłaszczyzny, które wyznaczają kąt dwuścienny, nazywamy ścianami kąta dwuściennego, zaś ich wspólną krawędź – krawędzią kąta dwuściennego.

Kątowi dwuściennemu możemy przyporządkować jego miarę. Aby to zrobić prowadzimy w kącie dwuściennym płaszczyznę prostopadłą do jego krawędzi (kolor zielony na rysunku). Wyznaczy ona na ścianach kąta dwuściennego kąt płaski α, który nazywać będziemy kątem liniowym kąta dwuściennego.

Uwaga! Przykładem kąta dwuściennego mogą być ściany pokoju łączące się w kącie, który jest właśnie jego krawędzią.

Wielościany

Wielościan jest to bryła geometryczna ograniczona przez powierzchnię utworzoną z wielokątów płaskich, które

  • mają wspólny bok lub wierzchołek albo nie mają żadnego punktu wspólnego,
  • każdy bok wielokąta jest bokiem wspólnym tylko dla dwóch wielokątów,
  • każdy wierzchołek jest wspólnym wierzchołkiem dla co najmniej trzech wielokątów.

Wielokąty te nazywamy ścianami wielościanu, ich boki krawędziami wielościanu, a ich wierzchołki wierzchołkami wielościanu.

 

wielościan 222


Wielościan składający się z jednakowych wielokątów foremnych, w których sąsiednie pary ścian tworzą równe kąty dwuścienne nazywamy wielościanem foremnym.

wielościan półforemny 222

Wielościan zbudowany z różnych wielokątów foremnych to wielościan półforemny.

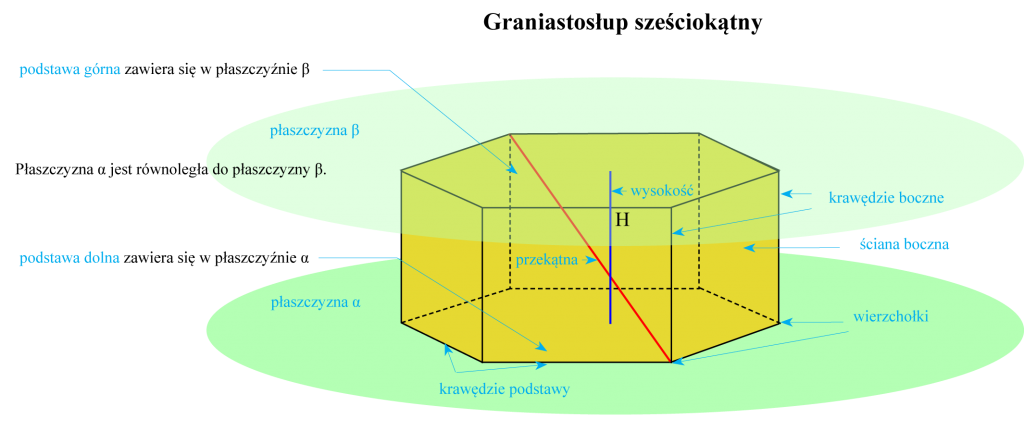
Graniastosłup

Graniastosłup jest to wielościan,

  • którego ściany zwane podstawami, są dowolnymi wielokątami przystającymi (jeden jest lustrzanym odbicie drugiego)i zawierają się w dwóch płaszczyznach równoległych,
  • jego ściny boczne są równoległobokami mającymi po jednej krawędzi z podstawą górną i podstawą dolną,
  • krawędzie boczne są wzajemnie równoległe i są równej długości,

Graniastosłup prosty jest to graniastosłup, którego ściany boczne są prostokątami a krawędzie boczne są prostopadłe do jego podstawy.

Wysokości graniastosłupa prostego jest równa długości jego krawędzi bocznej.

Graniastosłup foremny (prawidłowym) jest to graniastosłup prosty, którego podstawami są wielokąty foremne (mającym równe boki oraz kąty) np. trójkąt równoboczny, kwadrat.

Przekątne graniastosłupa są to odcinki łączą przeciwległe wierzchołki ale tylko te, które nie leżą do jednej ściany.

Wysokością graniastosłupa jest odcinek łączący podstawę górną i podstawę dolną, prostopadły do nich.

Płaszczyzną przekątną graniastosłupa jest to płaszczyzna łącząca co najmniej trzy wierzchołki graniastosłupa i nie zawierająca jego ściany.

Graniastosłup sześciokątny

  • Pole powierzchni bocznej graniastosłupa jest sumą powierzchni pół wszystkich ścian bocznych (bez podstawy dolnej i górnej).
  • Pole powierzchni całkowitej graniastosłupa
    Pole powierzchni graniastosłupa jest to suma pól wszystkich ścian bocznych i dwóch podstaw (jest ono równe polu powierzchni jego siatki).

Pc = 2Pp + Pb

Pc – pole powierzchni całkowitej
Pp – pole powierzchni podstawy
Pb – suma pól ścian bocznych

  • Objętość graniastosłupa

V = Pp · H

V – objętość
Pp – pole powierzchni podstawy
H – wysokość

 

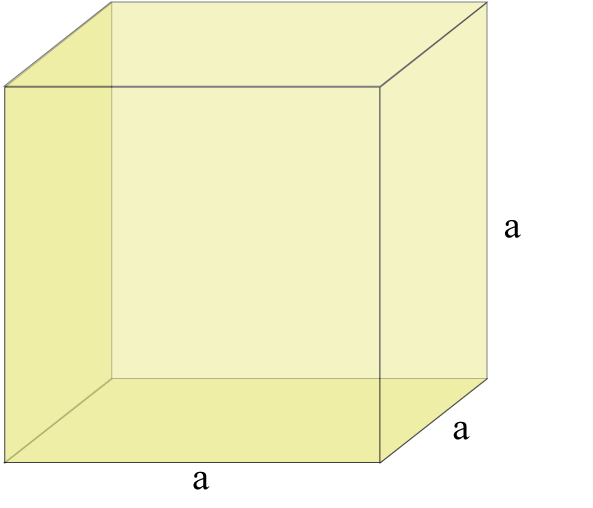
Sześcian

Sześcian jest szczególnym przypadkiem prostopadłościanu, w który wszystkie krawędzie są równe.
Każdy bok sześcianu jest kwadratem.

sześcian 22

  • Objętość sześcianu


a – długość krawędzi

  • Pole powierzchni sześcianu


a – długość krawędzi

 

Prostopadłościan

Prostopadłościan to równoległościan, którego każda ściana jest prostokątem (w tym podstawa, bo to jest jedna ze ścian prostopadłościanu).

  • W prostopadłościanie wszystkie przekątne są równe.
  • Kąty między każdymi dwoma ścianami o wspólnej krawędzi mają miarę równą 90° .
  • W prostopadłościanie dowolne dwie ściany są do siebie albo równoległe, albo prostopadłe.
  • Objętość prostopadłościanu

V = a·b·c
a, b, c – długość krawędzi

  • Pole powierzchni prostopadłościanu

S = 2ab + 2bc + 2ac
a, b, c – długość krawędzi

Siatka graniastosłupa

Siatka graniastosłupa jest to obraz prostopadłościanu po „rozwinięciu” jego ścian na płaszczyźnie.
Uwaga! Pole powierzchni całkowitej graniastosłupa jest równe polu jego siatki.
Poniżej na rysunku siatka graniastosłupa prawidłowego o podstawie sześciokąta.

siatka prostopadłościanu 22

Siatka prostopadłościanu jest to obraz prostopadłościanu po „rozwinięciu” jego ścian na płaszczyźnie.

 

Graniastosłup pochyły

  • Graniastosłup pochyły to graniastosłup, w którym krawędzie boczne nie są prostopadłe do podstaw.
    Krawędzie graniastosłupów pochyłych tworzą z płaszczyznami podstaw jednakowe kąty.
  • Ich ściany to ściany to równoległoboki.
  • W graniastosłupie pochyłym długość wysokości jest mniejsza od długości krawędzi bocznej.

–

graniastosłupy pochyłe

  • Objętość graniastosłupa pochyłego

V = Pp · H

V – objętość
Pp – pole powierzchni podstawy
H – wysokość



Ostrosłup

Ostrosłupem nazywamy wielościan, którego jedna ściana zwana podstawą, jest dowolnym wielokątem, a pozostałe ściany są trójkątami o wspólnym wierzchołku, zwanym wierzchołkiem ostrosłupa.

  • Ostrosłupy mają tylko jedną podstawę z wyjątkiem czworościanu, w którym każda ze ścian może być podstawą.
  • Ostrosłup o podstawie n-kątnej nazywamy ostrosłupem n-kątnym (np. ostrosłup czterokątny, ostrosłup dziesięciokątny itp.).

ostrosłup prawidłowy

Wysokość ostrosłupa jest to odcinek łączący wierzchołek ostrosłupa z jego podstawą pod kątem prostym.

Powierzchnią boczną graniastosłupa jest suma wszystkich ścian bocznych.

Polem podstawy jest pole wielokąta, który stanowi podstawę graniastosłupa.

Pole powierzchni całkowitej jest suma pół wszystkich ścian ostrosłupa (bocznych i podstawy).

Ostrosłupem prawidłowym jest ostrosłup, którego podstawą jest wielokąt foremny, a jego krawędzie są równej długości.

  • Ściany boczne ostrosłupa prawidłowego są przystającymi trójkątami równoramiennymi.
  • Wysokość ostrosłupa prawidłowego łączy się w podstawie ze środkiem okręgu opisanego na niej.

Czworościanem foremnym nazywamy ostrosłup prawidłowy, którego podstawa i trzy ściany boczne są trójkątami równobocznymi.

 

czworościan foremny

  • Pole powierzchni ostrosłupa
    Pole powierzchni całkowitej ostrosłupa jest równe sumie pola podstawy i pól ścian bocznych.

Pc = Pp + Pb

Pc – pole powierzchni całkowitej
Pp – pole powierzchni podstawy
Pb – pole powierzchni bocznej

  • Objętość ostrosłupaobjętość ostrosłupa
    V – objętość
    Pp – pole powierzchni podstawy
    H – wysokość ostrosłupa