Narysujmy na płaszczyźnie dwie różne półproste o wspólnym początku, nie należące do jednej prostej. Płaszczyzna została podzielona w ten sposób na dwa obszary, z których każdy nazywamy kątem.
Wspólny początek półprostych nazywamy wierzchołkiem kąta, a owe półproste – jego ramionami.
Oznaczenia kątów:
- trzyliterowe
: ramię, wierzchołek, ramię oznaczają wnętrze kąt - jednoliterowe – greckie litery α, β, γ, δ
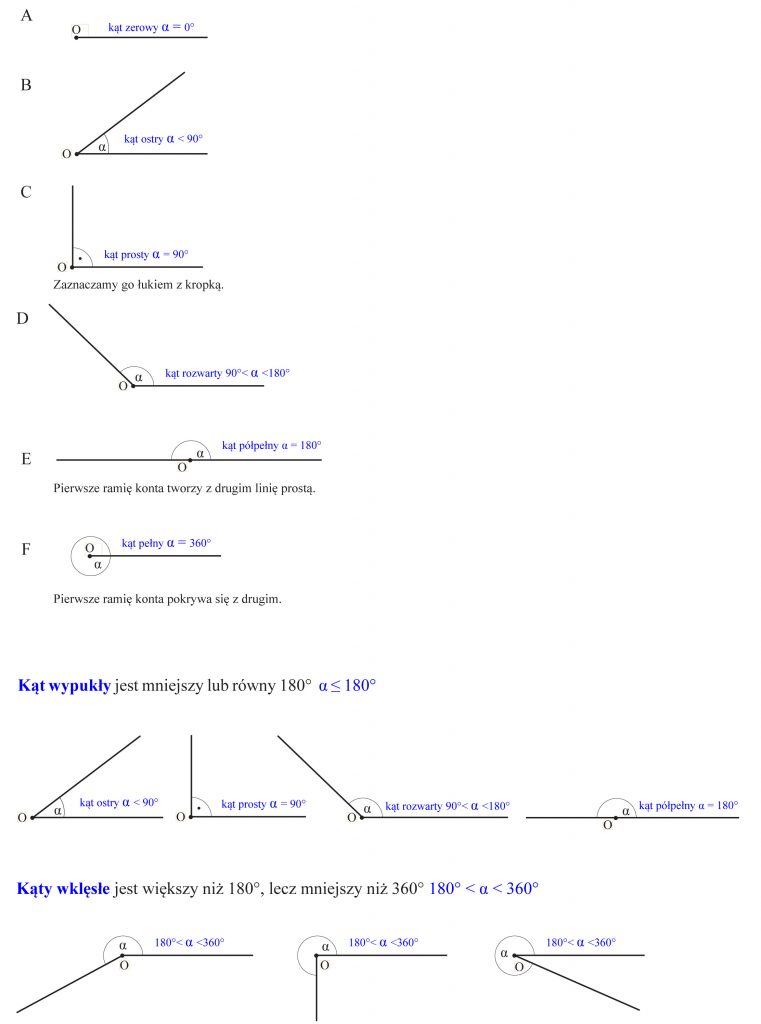
Rodzaje kątów
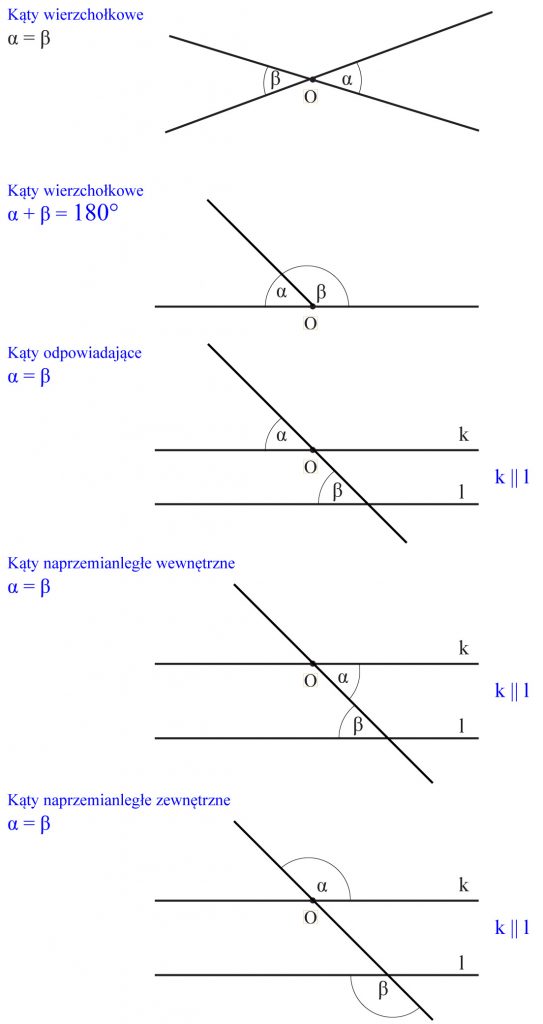
Przy rozwiązywaniu zadań potrzebna też będzie znajomość kątów:
Zadania
Rysunek do zadania 1. i 2.
1. Częścią wspólną odcinków AC i CD jest:
A. odcinek BC
B. punkt C
C. odcinek AC
D. odcinek CD
2. Częścią wspólną półprostych CA i BD jest:
A. półprosta BD
B. półprosta CA
C. odcinek BC
D. odcinek AB
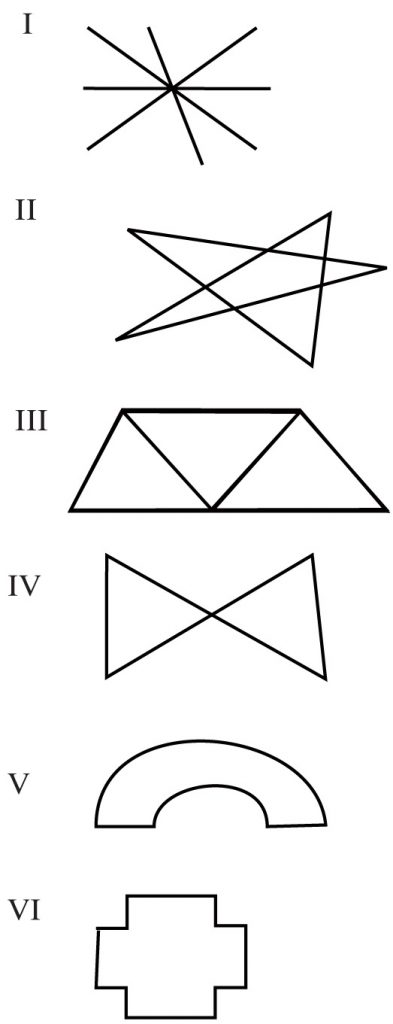
3. Które z figur są łamanymi:
A. I, II, III
B. II, III, IV, VI
C. II, III, VI
D. wszystkie
Rysunek do zadań: 4., 5., 6., 7.
4. Kątami wierzchołkowymi są:
A. 3 i 4
B. 2 i 3
C. 2 i 4
D. 1 i 2
5. Kątami przyległymi są:
A. 3 i 4
B. 2 i 3
C. 2 i 4
D. 1 i 2
6. Kątami odpowiadającymi są:
A. 3 i 4
B. 2 i 3
C. 2 i 4
D. 1 i 2
7. Kątami naprzemianległymi są:
A. 3 i 4
B. 2 i 3
C. 2 i 4
D. 1 i 2
8. Jeden z kątów przyległych jest 2 razy większy od drugiego. Większy z tych kątów ma miarę:
A. 60°
B. 90°
C. 135°
D. 120°
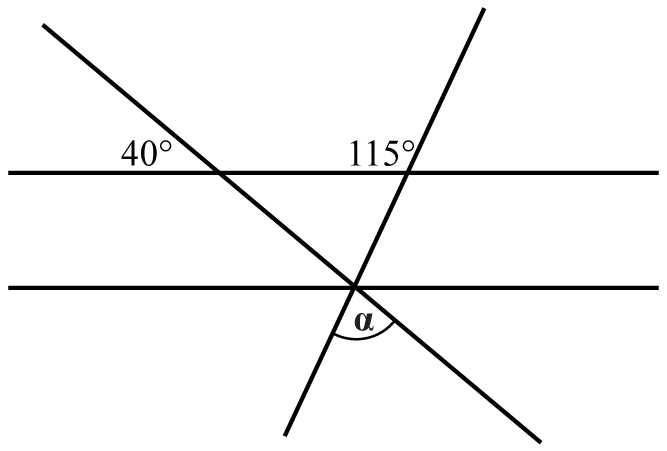
9. Proste k i l są równoległe. Kąt ma miarę:
A. 40°
B. 75°
C. 65°
D. 80°
Odpowiedzi:
1. B, 2. C, 3. C, 4. B, 5. D, 6. A, 7. C, 8. D, 9. B