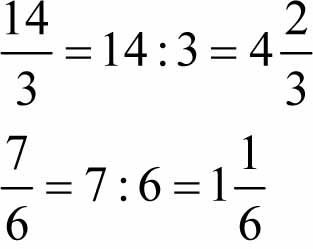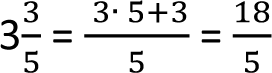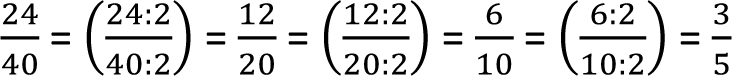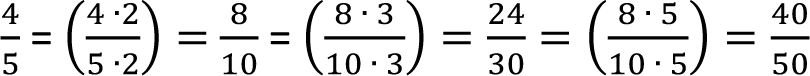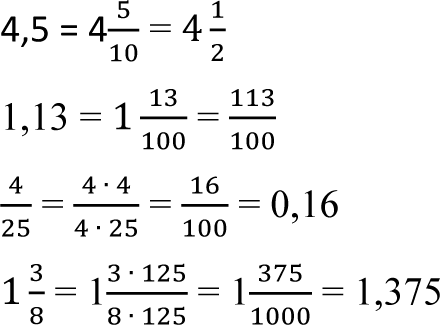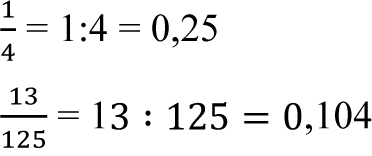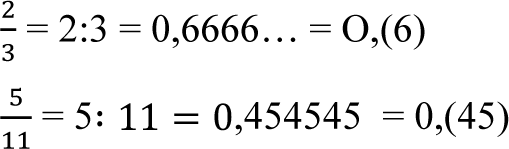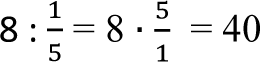Co to jest ułamek?
Ułamek traktujemy jako część jedności albo iloraz dwóch liczb całkowitych. Ułamkiem będzie fragment każdej z tych figur, które traktujemy jako całość.

Mianownik wskazuje na ile części podzielona jest całość. W przypadku tabliczki czekolady (na rys. poniżej), podzielona jest na 36 części (kostek).
Każda kostka czekolady będzie ułamkiem całej tabliczki (przy okazji powtórka ze słowotwórstwa: żeby zjeść kawałek czekolady, trzeba go najpierw ułamać z całości – i stąd nazwa ułamek).
Ułamki tak jak liczby całkowite – mają swoje miejsce na osi liczbowej:
Ułamek właściwy, niewłaściwy i mieszany
- Ułamek nazywamy właściwym, jeżeli licznik jest mniejszy od mianownika, np.
- Niewłaściwym nazywamy ułamek, w którym mianownik jest równy lub większy od licznika, np.
- Ułamek mieszany składa się z liczby i ułamka właściwego (jest ich sumą).
Wyłączanie jedności
Ułamek niewłaściwy możemy zamienić na ułamek mieszany, w którym jedności zostają wyłączone przed ułamek.
Zapamiętaj
Aby zamienić ułamek niewłaściwy na mieszany musimy podzielić licznik przez mianownik przez co uzyskamy część całkowitą ułamka, reszta która nam zostaje z dzielenia daje nam licznik części ułamkowej, a mianownik pozostaje bez zmian.
- Można też wykonać czynność odwrotną, czyli zamienić ułamek mieszany na niewłaściwy, np.
Skracanie ułamków
Skracanie ułamków polega na dzieleniu licznika i mianownika ułamka przez taką sama liczbę różną od zera. Jeżeli tabliczka czekolady ma dziesięć kostek, a Ty zjadłeś cztery, to otrzymujesz ułamek, w którym licznik = 4, a mianownik = 10. Obie liczby można podzielić przez dwa i w ten sposób zmniejszyć ułamek tak, by w liczniku było 2, a w mianowniku 5. Ten zabieg nie jest konieczny zawsze, ale przydaje się przy sprowadzaniu ułamków do wspólnego mianownika.
Przykład:
Rozszerzanie ułamków
Rozszerzanie ułamków polega na mnożeniu licznika i mianownika ułamka przez taką samą liczbę różną od zera. Jest to zabieg odwrotny od skracania i również jest przydatny przy szukaniu wspólnego mianownika.
Przykład:
Porównywanie ułamków
Przy porównywaniu ułamków należy pamiętać, że:
- Z dwóch ułamków o równych licznikach ten jest większy, który ma mniejszy mianownik.
- Z dwóch ułamków o równych mianownikach ten jest większy, który ma większy licznik.
Jeżeli ułamki mają różne liczniki i różne mianowniki, należy sprowadzić je do jednakowego mianownika albo do jednakowego licznika i dopiero wtedy porównać. Do tego przydaje się znajomość zasad skracania i rozszerzania ułamków.
Dodawanie i odejmowanie ułamków
Sprowadzenie do jednakowego mianownika przydaje się także przy dodawaniu i odejmowaniu ułamków o różnych mianownikach. Żeby wykonać odejmowanie lub dodawanie koniecznie trzeba sprowadzić ułamki do tego samego mianownika a następnie dodać lub odjąć liczniki pozostawiając mianownik bez zmian.
Kiedy odejmujemy ułamki mieszane najpierw musimy sprowadzić części ułamkowe do wspólnego mianownika, a następnie odejmujemy osobno liczby całkowite i osobno części ułamkowe.
Jeśli licznik ułamka odejmowanego jest większy od licznika ułamka od którego odejmujemy musimy jego wartość powiększyć o część całkowitej jedności. W przykładzie poniżej jedność to 15/15 dlatego do licznika dodajemy 15 (10 + 15 = 25)
Mnożenie i dzielenie ułamków
Ułamki można również mnożyć i dzielić.
- Aby pomnożyć dwa ułamki, mnożymy przez siebie osobno ich liczniki i osobno mianowniki, a potem wpisujemy wyniki mnożenia odpowiednio jako licznik i mianownik iloczynu.
- Dzielenie ułamków polega na mnożenie pierwszego ułamka przez odwrotność drugiego i dalej postępujemy jak przy mnożeniu.
Ułamki dziesiętne
Ułamek, którego mianownikiem jest 10, 100, 1000, … nazywamy dziesiętnym. Ułamki dziesiętne możemy zapisać jak ułamki zwykłe, ale częściej zapisujemy bez kreski ułamkowej, w tzw. układzie dziesiątkowym pozycyjnym, oddzielając przecinkiem część całkowitą od ułamkowej. Ułamki dziesiętne można dodawać, odejmować, mnożyć i dzielić. Można je też porównywać.
A tak zamieniamy ułamki dziesiętne na ułamki zwykłe, i na odwrót:
W przypadku ostatnim i przedostatnim stosujemy rozszerzenie ułamka do mianownika dziesiętnego.
Rozszerzanie ułamka nie zawsze jest wykonalne, stosujemy więc wtedy dzielenie licznika przez mianownik, np.:
Zapamiętaj!
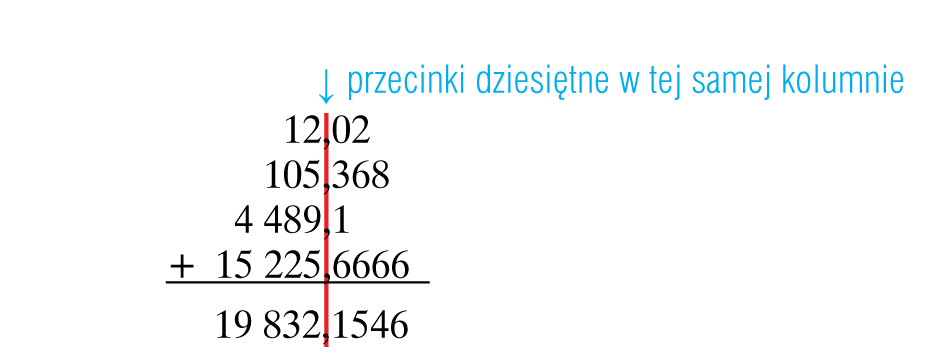
Ułamki dziesiętne dodajemy i odejmujemy tak jak liczby naturalne, musimy jednak pamiętać aby przecinki dziesiętne były w tej samej pionowej pozycji. pionowej pozycji.
Uwaga
Liczbą dziesiętną nazywamy ułamek dziesiętny o skończonej liczbie cyfr zapisany w dziesiątkowym systemie pozycyjnym.
Ułamki nieskończone, okresowe
Nie wszystkie ułamki zwykłe można zapisać w postaci ułamków dziesiętnych skończonych. Dają one rozwinięcie nieskończone np.
Są to rozwinięcia okresowe.
Uwaga!
Okresem nazywamy cyfrę lub grupę cyfr powtarzających się.
Czasami potrzebne są nam przybliżenia ułamków nieskończonych, wtedy stosujemy regułę:
- Jeżeli pierwsza z odrzucanych cyfr jest piątką lub więcej niż pięć, to ostatnią z pozostawionych powiększamy o 1. Np.: 1,34689 zaokrąglamy do części setnych więc: 1,34689 = 1,35.
- Jeżeli pierwsza z odrzucanych cyfr jest mniejsza od 5, wtedy ostatnią z pozostawionych zostawiamy bez zmian Np.: 0,851497=0,85.
Jak poznamy, który ułamek zwykły daje rozwinięcie dziesiętne skończone, a który nieskończone?
Jeżeli w rozkładzie mianownika ułamka na czynniki pierwsze występują tylko dwójki lub piątki, to ułamek daje rozwinięcie dziesiętne skończone. Jeśli natomiast w rozkładzie mianownika występują czynniki inne niż 2 lub 5, to rozwinięcie dziesiętne takiego ułamka jest nieskończone. I jest to zawsze ułamek okresowy.
Czasem okres ułamka jest wyjątkowo duży, ale jest to okres czyli w którymś kolejnym etapie dzielenia cyfry zaczną się po powtarzać, np.: 2,842105263157894736/8421… = 2,(842105263157894736)
Zadania z ułamkami
Przy omawianiu ułamków nie sposób pominąć trzech typów zadań, które wiążą się nierozerwalnie z tym tematem.
- Obliczanie ułamka danej liczby.
- Obliczanie liczby z danego jej ułamka.
- Obliczanie jakim ułamkiem jednej liczby jest druga liczba.
Przykładowe zadanie:
Klasa liczy 40 uczniów. 8 z nich jest dzisiaj nieobecnych i stanowi to 1/5 wszystkich uczniów. Występują tu trzy wielkości:
- liczebność klasy – 40
- ilość uczniów nieobecnych – 8
- ułamek nieobecnych – 1/5
W zadaniach tego typu dwie wielkości są zawsze dane, a trzecią trzeba wyliczyć.
Typ 1.
Jeżeli dane są:
- liczebność klasy – 40
- ułamek nieobecnych – 1/5
i trzeba obliczyć ilu uczniów jest nieobecnych – to jest to obliczanie ułamka danej liczby. Robimy to w sposób następujący:
Typ 2.
Jeżeli dane są:
- ułamek nieobecnych – 1/5
- liczba nieobecnych uczniów – 8
i trzeba obliczyć ilu uczniów liczy klasa, to jest to obliczanie liczby z danego jej ułamka.
Typ 3.
I wreszcie jeżeli dane są::
- liczebność kasy – 40
- ilość uczniów nieobecnych – 8
i trzeba wyliczyć, jaki ułamek, jest to obliczanie, jakim ułamkiem ilości wszystkich uczniów jest ilość uczniów nieobecnych.