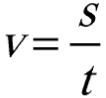1. Co to jest ruch?
Poruszają się gwiazdy i planety, zwierzęta i samochody. Poruszasz się Ty. Poruszają się najmniejsze cząstki materii. Słowem – porusza się wszystko.
Jak zdefiniować ruch?
Jeśli idziesz ulicą, mijasz domy, ludzi – zmieniasz swoje położenie. Zatem ruch to zmiana położenia poruszającego się ciała.
Wyobraź sobie ciało w zupełnie pustej przestrzeni. Cały wszechświat to jedno ciało. Czy ono się porusza? Czy można to jakoś sprawdzić, skoro wokół nie ma nic, do czego można byłoby odnieść położenie ciała? Nie, bo nie można byłoby w żaden sposób określić położenia. A skoro położenia, to i jego zmian. Dlatego należałoby naszą definicję uzupełnić:
Zapamiętaj!
Ruch to zmiana położenia względem innych ciał.
Jeśli idę ulicą, to zmieniam położenie względem ulicy, jej charakterystycznych punktów. Księżyc porusza się względem Ziemi – zmienia położenie w stosunku do niej, ale porusza się także względem Słońca.
Jeżeli ciało nie zmienia swego położenia, nie porusza się, mówimy, że jest w spoczynku.
2. Co to jest układ odniesienia?
Takie ciało (lub układ ciał), które uznajemy w naszych rozważaniach za nieruchome i w stosunku do niego określamy zarówno położenie, jak i ruch innych ciał, nazywamy układem odniesienia.
Przykład:
- Ziemia krąży wokół Słońca.
Względem jakiego układu odniesienia jest rozpatrywany?
Układem odniesienia jest Słońce, ale Ziemia porusza się również względem innych planet Układu Słonecznego. Każda z tych planet też może być układem odniesienia. Względem Słońca ruch Ziemi będzie się przedstawiał najprościej i na tym polega przewaga tego układu odniesienia nad innymi.
- Samochód jedzie.
Naturalnym układem odniesienia jest Ziemia i nieruchome względem niej obiekty (drzewa, domy). Ale można opisywać jego ruch względem innego układu, np. innego samochodu.
Skojarz!
Ten sam ruch może być rozpatrywany z punktu widzenia różnych układów odniesienia.
3. Jakie ciało należy wybrać na układ odniesienia?
Teoretycznie można wybrać każde. W praktyce jednak kierujemy się wygodą.
Jeśli chcemy opisać ruch elektronu w lampie kineskopowej telewizora, to po co opisywać go z punktu widzenia Słońca czy przejeżdżającego samochodu? Najlepszym kandydatem na układ odniesienia jest w tym przypadku telewizor, bo ruch elektronu jest względem takiego układu odniesienia najprostszy.
4. Po co wprowadza się układ współrzędnych?
Gdy chcemy dojść do stacji kolejowej, wystarczy nam informacja, że trzeba iść na lewo, potem prosto. W fizyce i naukach technicznych taki opis położenia jest za mało dokładny. Takiemu dokładnemu określaniu położenia i ruchu ciał służy układ współrzędnych.
Zapamiętaj!
- Układ współrzędnych na płaszczyźnie to dwie osie nawzajem prostopadłe.
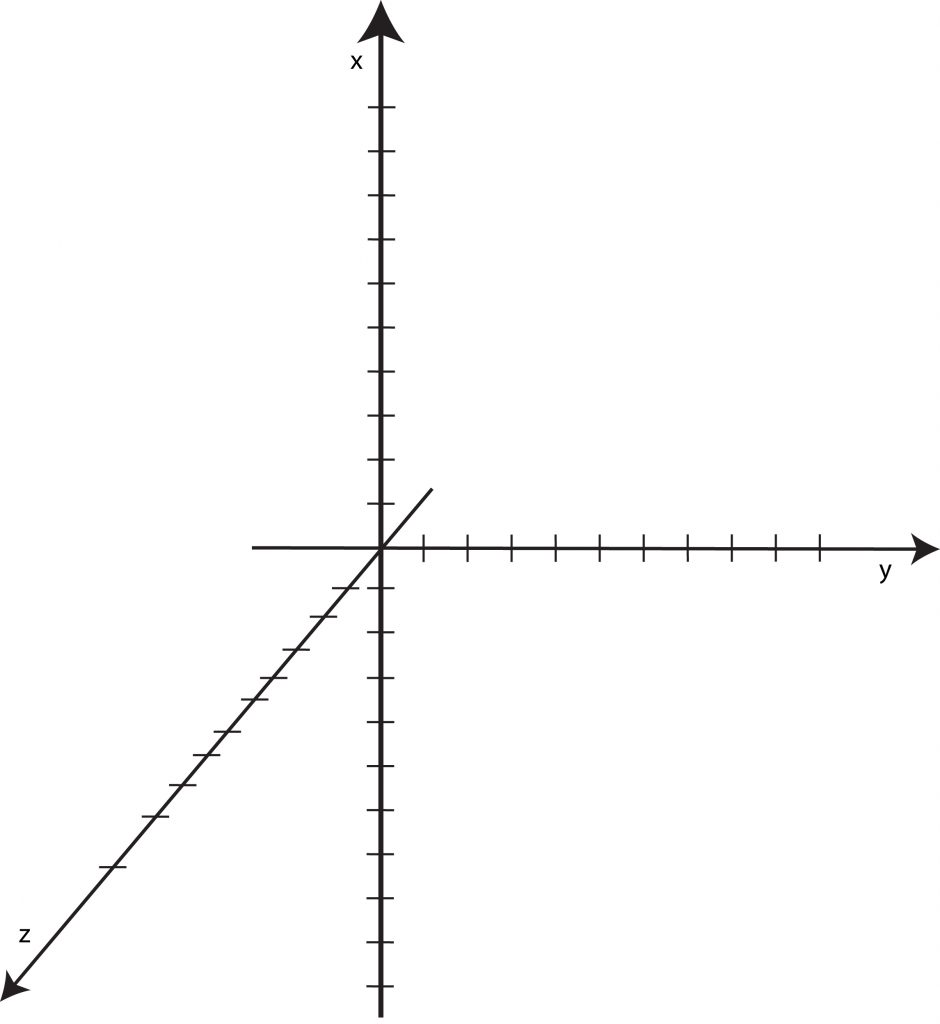
- Układ współrzędnych w przestrzeni – trzy proste prostopadłe przecinające się w jednym punkcie.
- Punkt przecięcia się osi nazywamy początkiem układu współrzędnych.
Dwuwymiarowy układ współrzędnych
Trójwymiarowy układ współrzędnych
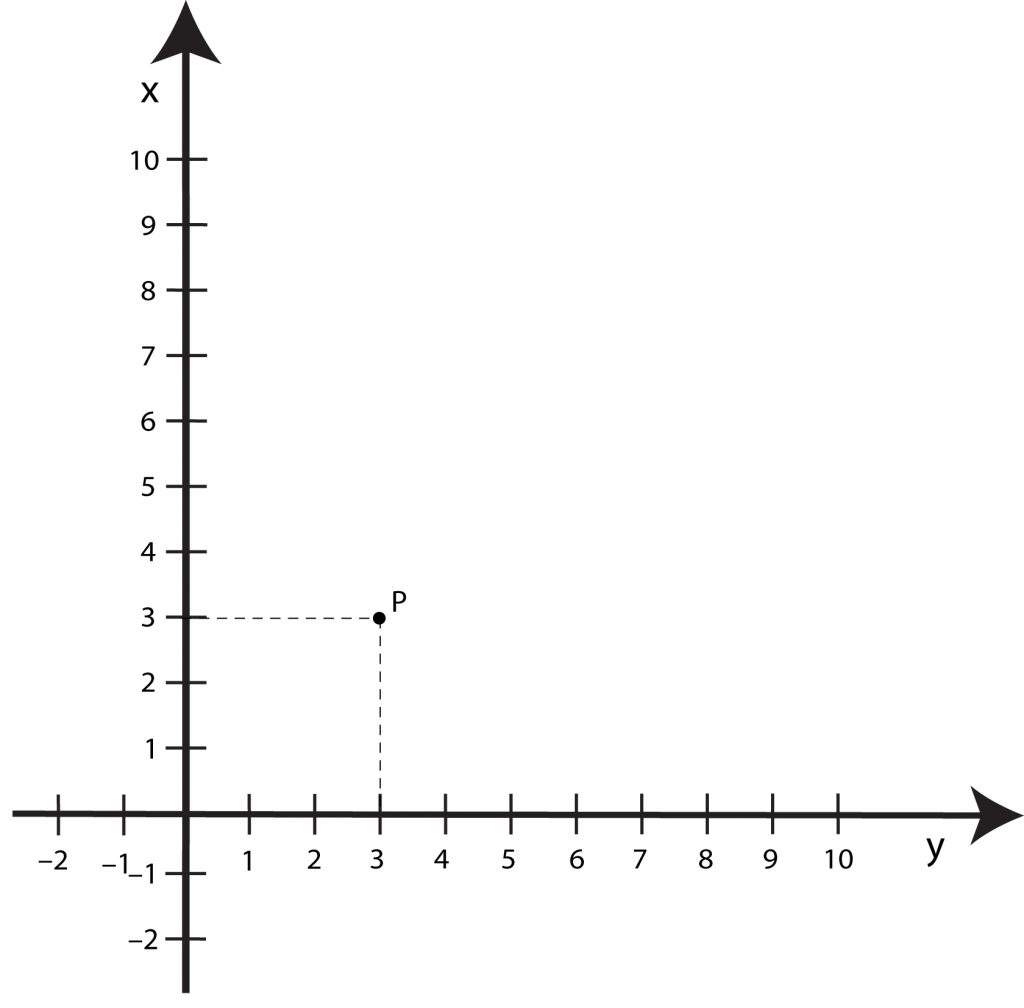
Jak określa się położenie punktu w takim układzie współrzędnych? Zróbmy to na przykładzie układu dwuwymiarowego:
- Punkt P ma współrzędne x = 3, y = 3.
- Zapisujemy to: P (4,3).
- Czytamy: punkt P ma współrzędne 3, 3.
Uwaga!
Współrzędna x-owa jest zawsze na pierwszym, a y-owa na drugim miejscu. W ten sposób określiliśmy położenie ciała za pomocą liczb. Gdy ciało porusza się, liczby będące jego współrzędnymi zmieniają się.
Zapamiętaj!
Aby opisać ruch jakiegoś ciała, wybieramy inne ciało, względem którego będziemy rozpatrywać jego ruch. Jest to wybór układu odniesienia. Dla precyzyjnego opisu tego ruchu z układem odniesienia wiążemy układ współrzędnych, kierując osie tak, jak nam wygodnie.
Przykład:
Chcemy opisać ruch owada w klasie.
Układem odniesienia będzie klasa, jej podłoga i ściany. Krawędzie, wzdłuż których stykają się ściany, w naturalny sposób wyznaczają osie układu współrzędnych. Jeszcze tylko wybór jednostki na osiach (może to być jeden metr) i możemy opisywać precyzyjnie ruch owada, podając, jak zmieniają się jego współrzędne z upływem czasu.
5. Co to jest tor ruchu?
Tor ruchu otrzymamy, jeśli połączymy linią kolejne położenia ciała. Jest to linia, jaką zakreśla ciało w trakcie swego ruchu.
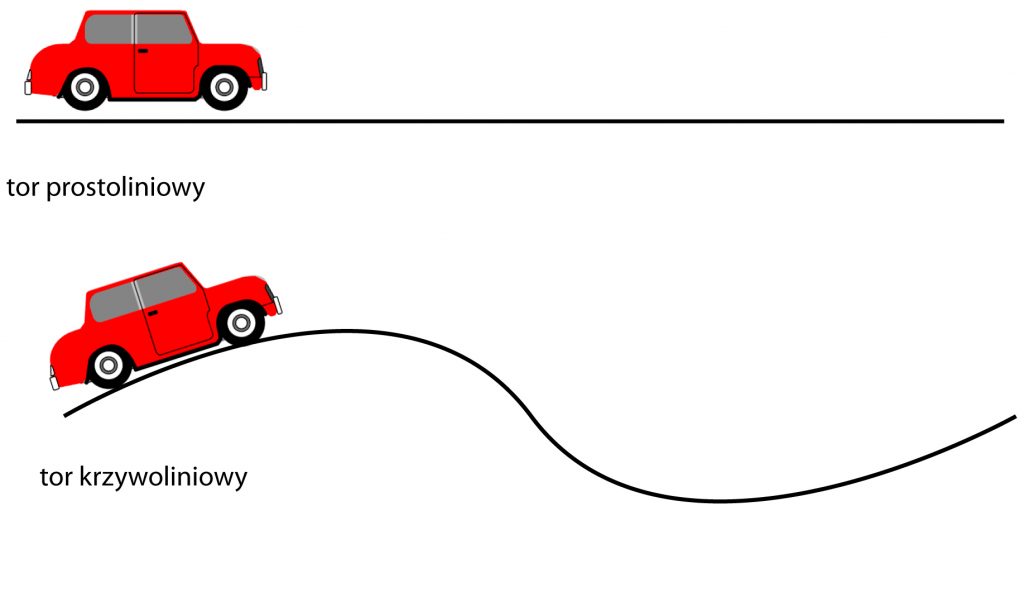
Ze względu na kształt toru ruchy możemy podzielić na:
- a) prostoliniowe – jeśli torem jest linia prosta,
- b) krzywoliniowe – jeśli ciało porusza się po jakiejś krzywej.
6. Co to znaczy, że ruch jest względny?
W zależności od tego, jaki wybierzemy układ odniesienia, to samo ciało może być w spoczynku lub poruszać się. W zależności od wyboru układu odniesienia ruch tego samego ciała może wyglądać bardzo różnie.
Przykład:
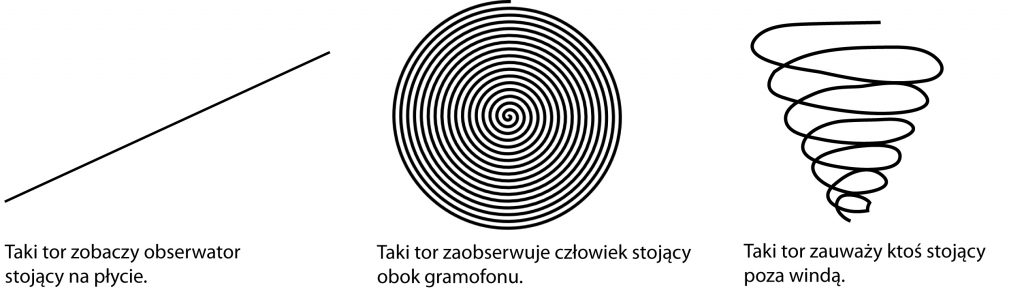
Wyobraźmy sobie gramofon, na którym leży obracająca się płyta (winylowa), umieszczony w poruszającej się w górę windzie o przezroczystych ściankach (można tam zajrzeć z zewnątrz). Po płycie (wzdłuż jej promienia) idzie biedronka. Owada obserwuje trzech ludzi: jeden stojący na płycie, drugi w windzie obok gramofonu, a trzeci poza szybem windy. Ruch biedronki dla tych trzech obserwatorów będzie zupełnie inny. Zupełnie inne będą zaobserwowane tory biedronki. Popatrz na rysunek:
7. Co to jest szybkość ciała?
To droga, jaką ciało przebyło, podzielona przez czas przebycia tej drogi. Bardzo podobną wielkością jest prędkość.
Definicje i prawa w fizyce zapisuje się w postaci wzorów. Zapiszmy w takiej skrótowej formie określenie szybkości:
v – szybkość,
s – droga,
t – czas przebycia drogi.
Szybkość, jak łatwo się domyślić, mówi nam, czy ciało porusza się szybko, czy wolno.
Możesz spotkać się jeszcze z pojęciem średniej szybkości. Nie musisz się tym szczególnie przejmować. Jest to po prostu stosunek całkowitej przebytej drogi do całkowitego czasu ruchu. Nie różni się to więc od podanej wyżej definicji.
Podstawową jednostką szybkości jest metr na sekundę. Często zapisuje się to tak:
Ciało poruszające się z taką szybkością przebywa w każdej sekundzie drogę jednego metra. Często używamy innych jednostek, na przykład kilometrów na godzinę.
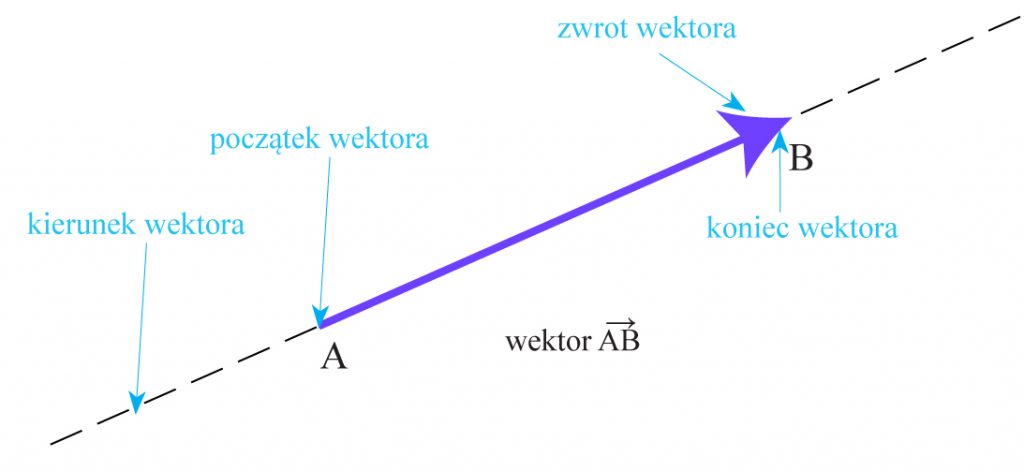
8. Czym charakteryzuje się wielkość wektorowa?
Pewne wielkości fizyczne mają tylko wartości liczbowe. Aby poznać, jaka jest temperatura, masa, długość, wystarczy podać jedną liczbę. Inne – oprócz wartości – mają też kierunek i zwrot. Przykładem jest siła czy prędkość. Ciała mogą się różnić swą szybkością, ale by w pełni scharakteryzować ich ruch, należy jeszcze powiedzieć, w którą stronę ciało się porusza. Podobnie jest z siłą. Można nią działać mocniej lub słabiej, ale by wiedzieć o tym działaniu więcej, musimy jeszcze znać kierunek działania siły. Takie wielkości, które mają wartość, kierunek i zwrot, nazywamy wektorowymi. Można je przedstawić graficznie w postaci strzałki. Długość takiej strzałki reprezentuje wartość wektora, kierunek wektora to kierunek prostej, na której leży strzałka, a zwrot oznaczony jest grotem (to jest koniec wektora). Początek wektora mówi nam, jakiego ciała dotyczy wielkość wektorowa. Jeśli na przykład wektor oznacza siłę przyłożoną do jakiegoś ciała, to początek tego wektora jest właśnie w tym ciele.
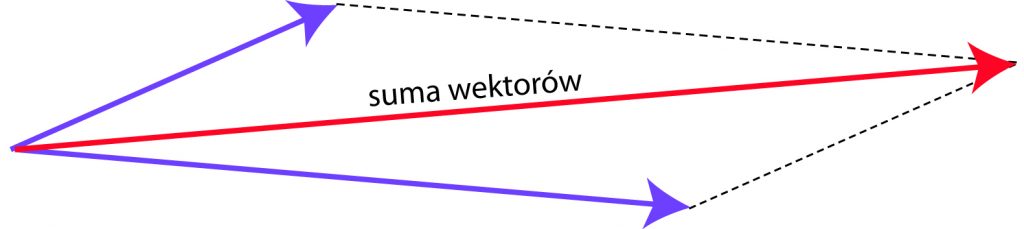
Załóżmy, że pewne ciało ma masę 3 kg. Jeżeli dołożymy jeszcze 2 kg, to razem na pewno będą mieć masę 5 kg. Masy dodają się jak zwykłe liczby. Czy prędkości lub siły dodają się w ten sposób? Otóż nie! Jeżeli na krzesło podziałam siłą 4 N, a potem dodatkowo jeszcze 3 N, to całkowita siła działająca na krzesło wcale nie musi wynosić 7 N. Tak jest tylko w tym szczególnym przypadku, gdy siły są zgodnie skierowane (mają ten sam kierunek i zwrot). W innych wypadkach całkowita siła będzie miała inną wartość, zależną od tego, jak siły są względem siebie skierowane. Siły nie dodają się jak liczby. To samo dotyczy np. prędkości. Dlatego wprowadza się wielkości wektorowe. One nie dodają się jak liczby. A jak? Popatrzmy na rysunek:
By dodać dwa wektory, budujemy z nich równoległobok, taki jak na rysunku. Suma wektorów jest tą przekątną równoległoboku, która ma początek tam, gdzie dodawane wektory. Okazuje się, że tak samo dodają się prędkości i siły. Wektory oznaczamy literą ze strzałką u góry, albo pogrubioną czcionką. Np. ![]() lub a.
lub a.
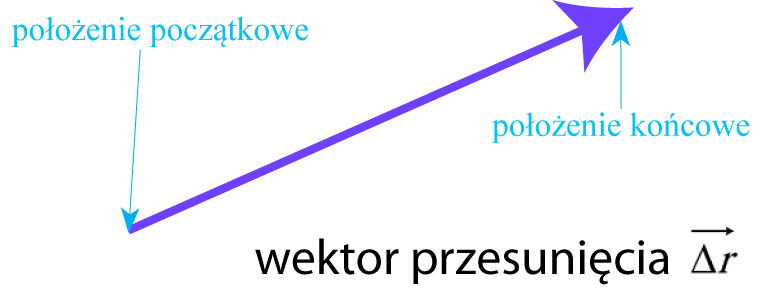
9. Jak jest określony wektor przesunięcia (przemieszczenia)?
Wyobraź sobie, że się poruszasz. Startujesz z punktu A, kończysz w punkcie B. Te dwa punkty, początkowy i końcowy można połączyć wektorem.
Zapamiętaj!
Wektor, który łączy początkowe i końcowe położenie poruszającego się ciała, nazywamy wektorem przesunięcia (albo przemieszczenia). Oznaczamy go ![]() .
.
Po co nam wektor przesunięcia?
Po to, żeby móc napisać określenie wektora prędkości (patrz punkt 11). Wartość wektora przesunięcia to po prostu odległość między początkowym i końcowym położeniem ciała. Mierzy się w jednostkach długości (metrach, centymetrach itd.). Jeśli ciało poruszało się po linii prostej, wartość wektora przesunięcia jest równa po prostu przebytej drodze.
10. Co to jest prędkość?
Definicja wektora prędkości wykorzystuje wektor przesunięcia, który przed chwilą zdefiniowaliśmy. Prędkość to stosunek wektora przesunięcia do czasu, w którym to przesunięcie nastąpiło. Wielkość tę oznaczamy symbolem ![]() .
.
Tak określona prędkość mówi nam nie tylko, jak szybko się ciało porusza (o tym informuje nas wartość prędkości), ale też o kierunku ruchu ciała. Wektor prędkości wskazuje, w którą stronę porusza się ciało. Z tego wynika, że wektor prędkości jest styczny do toru, po którym porusza się ciało.
Zapamiętaj!
Podstawową jednostką prędkości jest metr na sekundę. Inne to kilometr na godzinę, centymetr na minutę itd.
11. Jaka jest różnica między szybkością i prędkością?
Prędkość to wektor, natomiast szybkość to wartość tego wektora. Szybkość informuje nas tylko, jaką drogę przebywa ciało w jednostce czasu, natomiast prędkość mówi nam oprócz tego, w jakim kierunku się ciało porusza.
12. Na czym polega ruch jednostajny prostoliniowy?
Ruch prostoliniowy to taki, którego torem jest linia prosta. Zaś jednostajny to taki, w którym szybkość jest stała. W ruchu jednostajnym prostoliniowym ciało nie przyspiesza, nie zwalnia ani nie skręca.
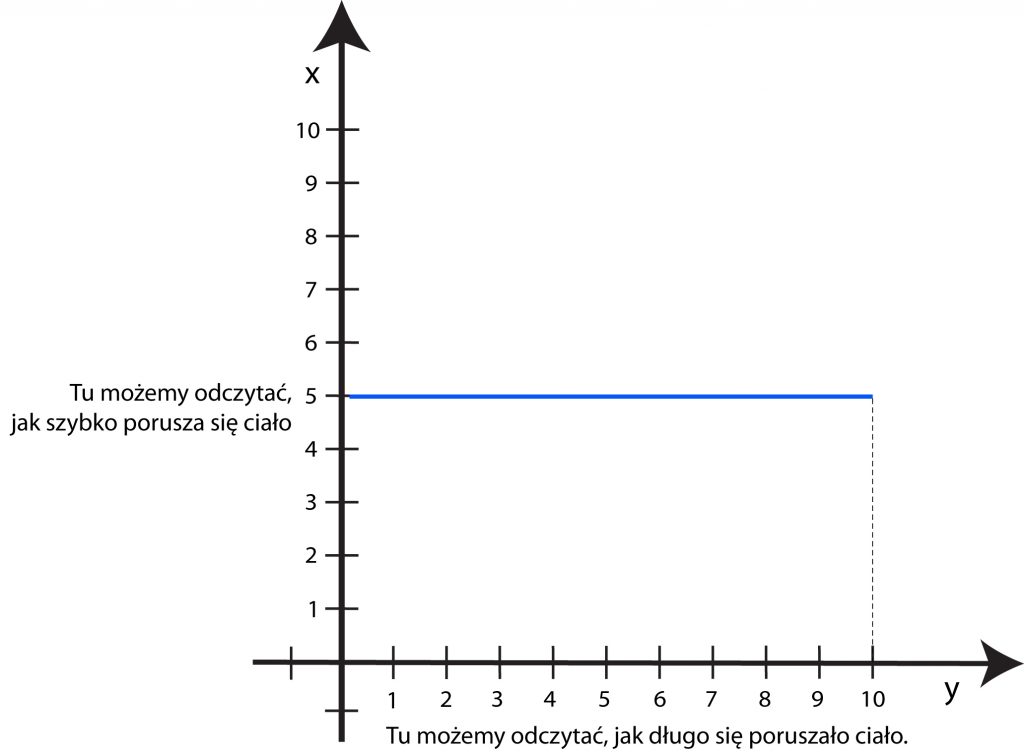
13. Narysuj wykres zależności prędkości od czasu w ruchu jednostajnym prostoliniowym.
Szybkość w takim ruchu jest stała, niezależna od czasu. Jak wygląda wykres stałej funkcji? To prosta poprowadzona poziomo w układzie współrzędnych:
14. Jak obliczyć drogę ciała poruszającego się ruchem jednostajnym?
Wystarczy szybkość ciała pomnożyć przez czas przebywania drogi.
droga = szybkość · czas
s = v · t
Jeśli samochód porusza się z szybkością 80 km/h i z taką szybkością jedzie przez 4 h (godziny), to przebędzie drogę
Uwaga!
Powyższy wzór jest prawdziwy tylko dla ruchu jednostajnego. Gdy ciało przyspiesza lub zwalnia, nie wolno z tego wzoru korzystać!
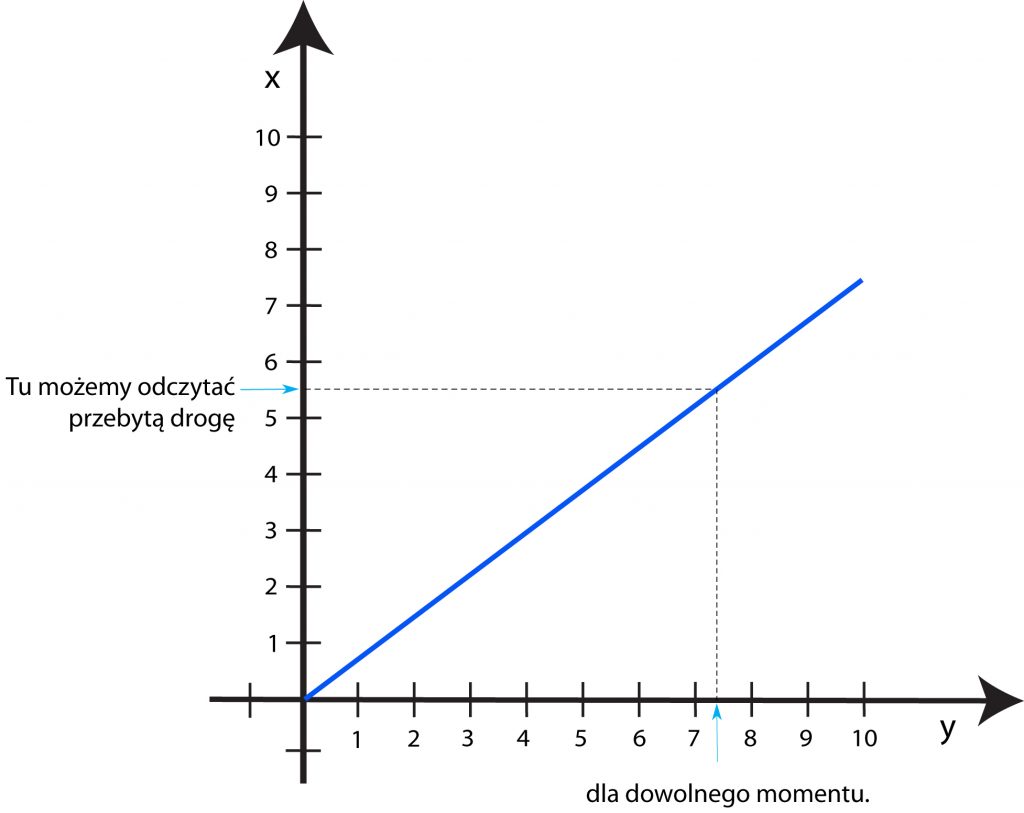
15. Jak wygląda wykres zależności drogi przebytej w ruchu jednostajnym od czasu?
Wzór mówi nam, jak rośnie przebyta droga, gdy upływa czas. Szybkość v jest stała w ruchu jednostajnym, można więc powiedzieć, że droga jest proporcjonalna do czasu. Wykres proporcjonalności wygląda tak:
Z takiego wykresu można odczytać szybkość ciała. Wystarczy odczytać na wykresie drogę (jest to pokazane na rysunku) i odpowiadający jej czas (to też widzimy na rysunku) i podzielić drogę przez czas (otrzymamy prędkość).
Takich zadań spodziewaj się na egzaminie gimnazjalnym!
Koniec wskazówki zegarowej porusza się po okręgu. Która ze strzałek poprawnie przedstawia wektor prędkości końca wskazówki?
A. I
B. II
C. III
D. IV
Rozwiązanie
Wektor prędkości to krótki sposób zapisania trzech informacji: które ciało się porusza (mówi o tym punkt zaczepienia wektora), jak szybko (to jego długość) i w którą stronę (kierunek i zwrot). Chcemy znać kierunek wektora prędkości koniuszka wskazówki zegarowej. Taki punkt porusza się (tak jak i pozostałe punkty wskazówki) po okręgu. Jeśli coś porusza się po okręgu, to oczywiście nieustannie zmienia kierunek ruchu. Ale w danym momencie kierunek ruchu wskazówki jest styczny do toru, czyli w tym wypadku okręgu. Mamy dwa wektory styczne do okręgu. Są to wektory I i III. Który z nich jest tym właściwym? Wszyscy wiemy, w którą stronę obracają się wskazówki. Jest to więc wektor III. Poprawna jest odpowiedź C.
Zadanie 2
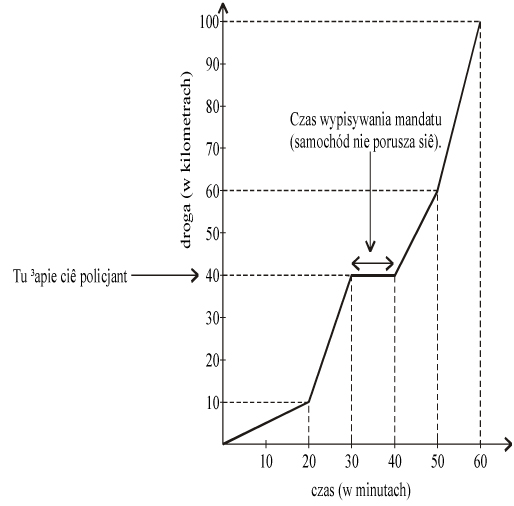
Wjechałeś na drogę szybkiego ruchu. Trasa ma długość 100 km. Przy wjeździe stoi taki oto znak:
Masz świetny samochód i marzysz o tym, by trochę poszaleć. Niestety, na 40. kilometrze łapie Cię policjant i wlepia mandat, twierdząc, że przekroczyłeś dozwoloną prędkość. Na szczęście (albo i nie) Twój nowoczesny samochód ma system rejestrujący, jaką drogę przebyłeś w zależności od czasu jazdy. Ta zależność jest widoczna na wykresie:
A. Mandat dostałeś niesłusznie, bo Twoja średnia szybkość na całej trasie wyniosła 100 km/h.
B. Słusznie dostałeś mandat, bo Twoja szybkość w momencie, gdy zauważył Cię policjant, przekraczała dozwoloną.
C. Mandat dostałeś niesprawiedliwie, ponieważ w momencie pomiaru policyjnym radarem miałeś poniżej 100 km/h na liczniku.
D. Mandat Ci się nie należał, bo Twoja średnia szybkość, zanim Cię zatrzymano, wyniosła poniżej 100 km/h.
Rozwiązanie
Na trasie nie wolno przekraczać 100 km/h. Zauważ, że policjant nie ma żadnej możliwości, by zmierzyć szybkość średnią na długim odcinku drogi już przebytej. Mierzy on szybkość, jaką ma kierowca w momencie pomiaru. Zmierzenie natomiast średniej szybkości na trasie, która dopiero ma być przebyta, wykracza poza czyjekolwiek możliwości. Zatem mandat płaci się za przekroczenie dozwolonej szybkości w momencie pomiaru. Ani wcześniej, ani później. Co z tego wynika? To, że odpowiedzi A i D są nieprawidłowe. Pozostaje więc odpowiedzieć, jaką szybkość miałeś na nieszczęsnym czterdziestym kilometrze. Otóż taką samą jak na czterdziestym kilometrze szybkość miałeś już od dziesiątego kilometra trasy. Dlaczego? Odpowiedni kawałek wykresu jest prostoliniowy. Wykres zależności drogi od czasu jest linią prostą dla ruchu jednostajnego, czyli zachodzącego ze stałą szybkością. Obliczmy szybkość samochodu między 10. a 40. kilometrem. Wystarczy (zgodnie z definicją) podzielić przebytą drogę przez czas jej przebycia. Z wykresu odczytujemy, że
- droga wynosi 40 km – 10 km = 30 km,
- a czas to 30 min – 10 min = 1/6 h.