Styczna do okręgu.
Wielokąty foremne.
Kąty środkowy i wpisany.
Zadanie 1
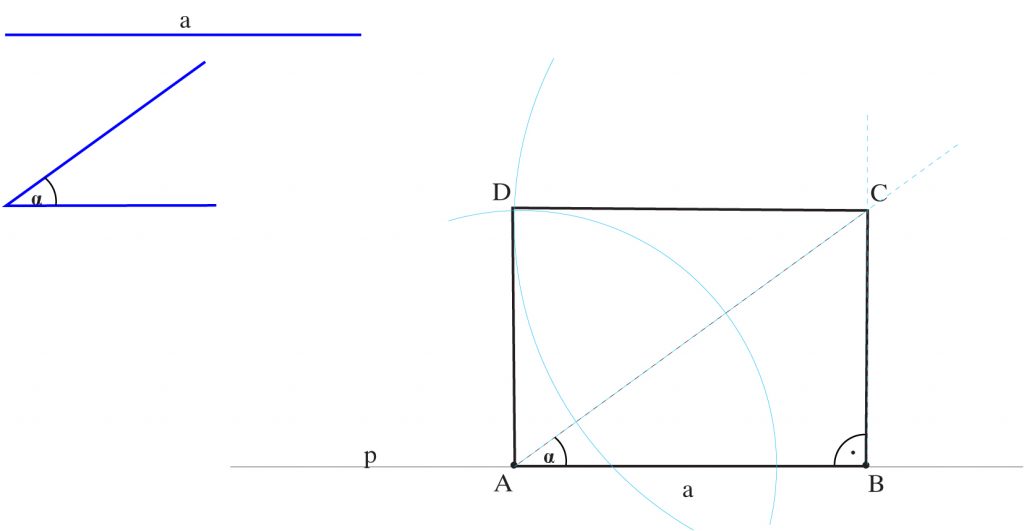
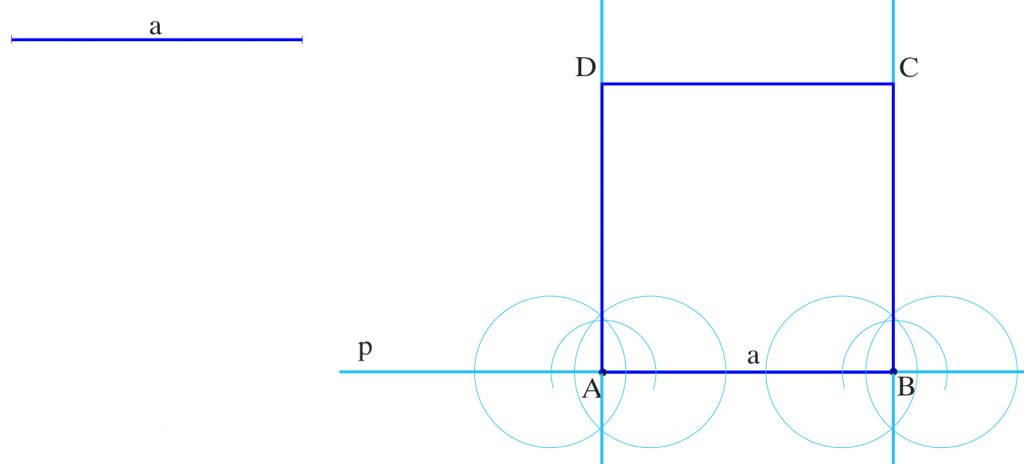
Zbuduj prostokąt mając dany jego bok a, oraz kąt ostry α zawarty między przekątną a bokiem a.
1.Na prostej p od punktu A odkładam bok a. Otrzymuję punkt B.
2. Przenoszę kąt α tak aby jego ramieniem była prosta p a wierzchołkiem punkt A. Otrzymuję drugie ramię kąta.
3. W punkcie B wystawiam prostopadłą do prostej p. W przecięciu prostopadłej z drugim
ramieniem kąta otrzymuję punkt C.
4. Z punktu C zataczam łuk rozwartością a, z punktu A zataczam łuk rozwartością odcinka BC. Otrzymuję punkt D.
5. Łączę punkt D z punktem A i z punktem C. Powstaje w ten sposób prostokąt ABCD.
Zadanie 2
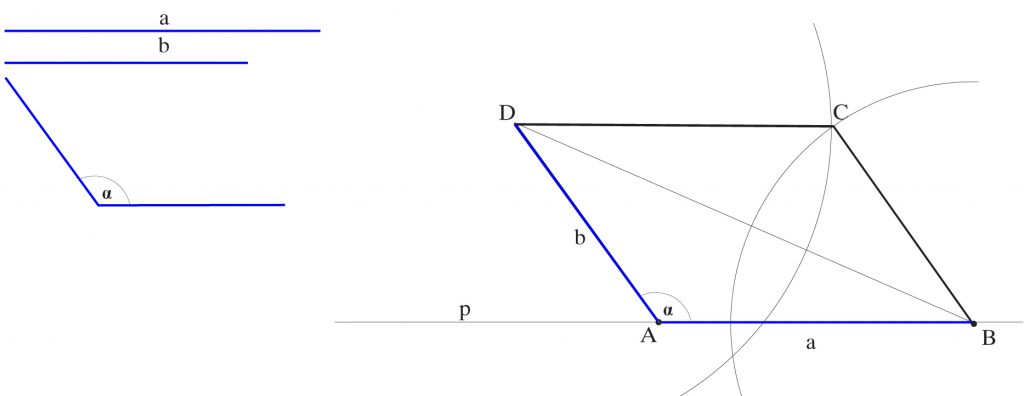
Zbuduj konstrukcyjnie równoległobok mając dane dwa jego boki a i b oraz kąt rozwarty α równoległoboku.
Analiza:
Buduję najpierw trójkąt ABD, a potem odszukuję punkt C.
1. Na prostej p od punktu A odkładam odcinek a. Otrzymuję punkt B.
2. Przenoszę kąt α na prostą p tak aby wierzchołek był w punkcie A. Powstaje drugie ramię kąta.
3. Na tym ramieniu kąta α odkładam odcinek b. Otrzymuję punkt D.
4. Z punktu D rozwartością odcinka a zataczam łuk; z punktu B rozwartością odcinka b zataczam łuk.
Z przecięcia łuków otrzymuję punkt C.
5. łączę punkty C z D i C z B. Powstaje równoległobok ABCD.
Zadanie 3
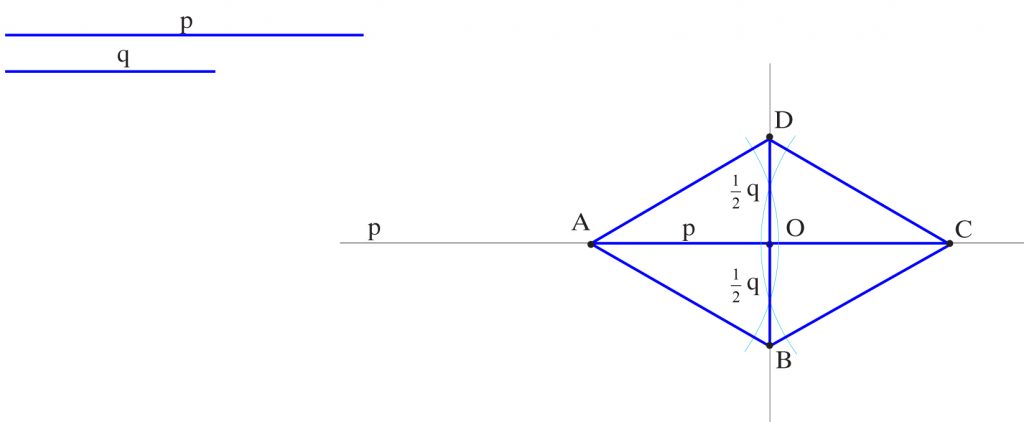
Nakreśl konstrukcyjnie romb mając jego obie przekątne p i q.
Analiza:
1. Na prostej m od punktu A odkładam odcinek p. Uzyskuję punkt C.
2. Teraz kreślę symetralną odcinka p. Na przecięciu orzymuję punkt O.
3. Od punktu O na symetralnej odkładam w górę i dół odcinek 1/2 q. Otrzymuję punkt B i punkt D.
4. Łączę punkty A, B, C, D. Powstaje romb ABCD.
Zadanie 4
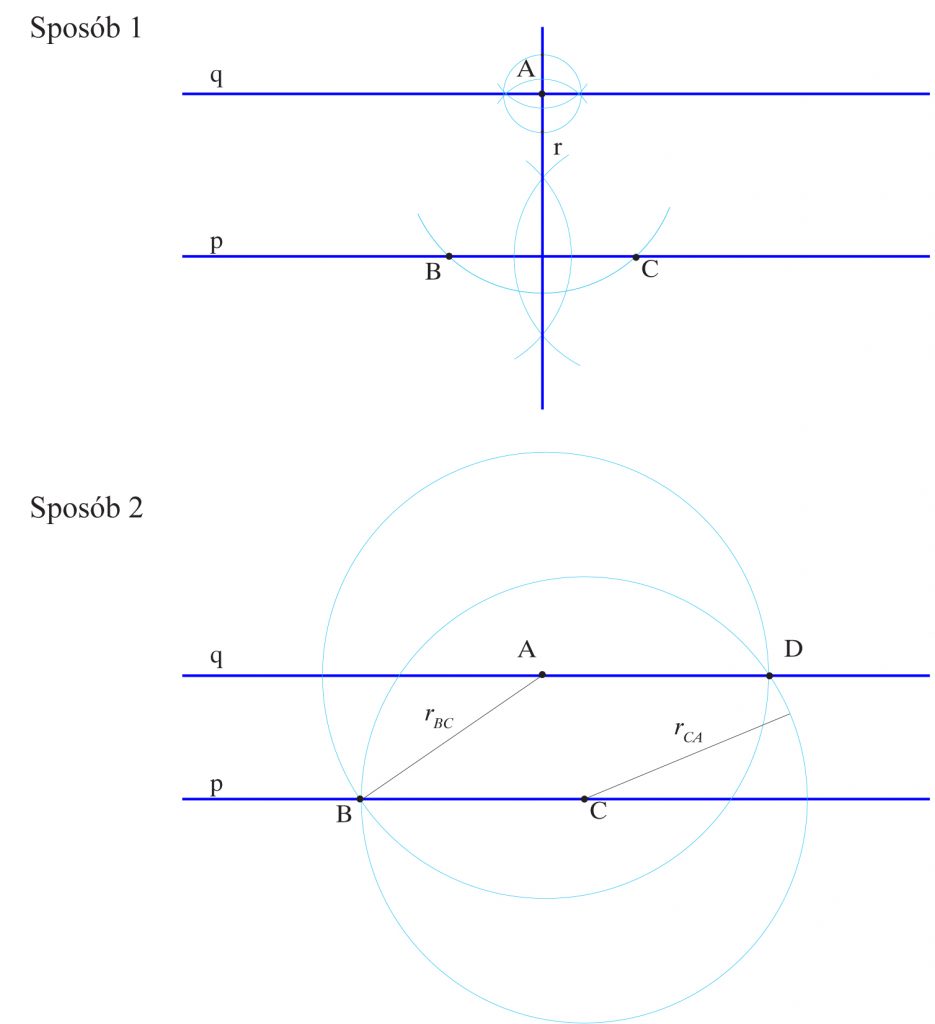
Przez punkt A nie leżący na prostej p nakreśl prostą q równoległą do p.
Sposób 1
Z punktu A prowadzę prostopadłą r do p.
Z punktu A prowadzę prostopadłą q do r. Proste p i q są równoległe.
Uwaga: Jeśli dwie proste p i q są prostopadłe do jednej i tej samej prostej r, to do siebie są równoległe.
Sposób 2
Na prostej p obieram dowolne punkty B i C takie, że B = C.
Z punktu A zataczam łuk promieniem BC i z punktu C zataczam łuk promieniem BA do przecięcia w punkcie D. Prosta AD jest równoległa do prostej p (konstrukcja równoległoboku).
Zadanie 5
Nakreśl trapez mając jego podstawy a i b oraz ramię c i kąt jaki tworzy ramię z dolną podstawą.
Analiza:
1. Na prostej p od punktu A odkładam odcinek a. Otrzymuję punkt B.
2. Przenoszę kąt α do punktu A na prostą p. Otrzymuję półprostą AM.
3. Na półprostej AM odkładam odcinek c. Otrzymuję punkt C.
4. Przez punkt C prowadzę półprostą q równoległą do prostej p.
5. Od punktu C na półprostej q odkładam odcinek b. Otrzymuję punkt D.
6. łączę punkty D i B. Powstaje trapez ABCD.
Zadanie 6
Nakreśl kwadrat mając jego bok a.
Opis konstrukcji:
Na prostej p odkładam od punktu A odcinek a otrzymując punkt B. W punktach A i B wystawiam prostopadłe, na których odkładam odcinek a od punktu A i od punktu B. Otrzymuję punkty C i D, łączę punkty C i D i otrzymuję kwadrat ABCD.
Zadanie 7
Zbuduj kwadrat mając daną jego przekątną p. (kwadrat jest rombem – patrz zad. 3).
Zadanie 8
Nakreśl konstrukcyjnie styczną do okręgu z punktu A
a) leżącego na okręgu
b) nie leżącego na okręgu.
Przypomnienie
- Styczna do okręgu to prosta mająca dokładnie jeden punkt wspólny z okręgiem.
- Styczna tworzy z promieniem kąt prosty w punkcie styczności.
Na tej własności opieramy konstrukcję stycznej.
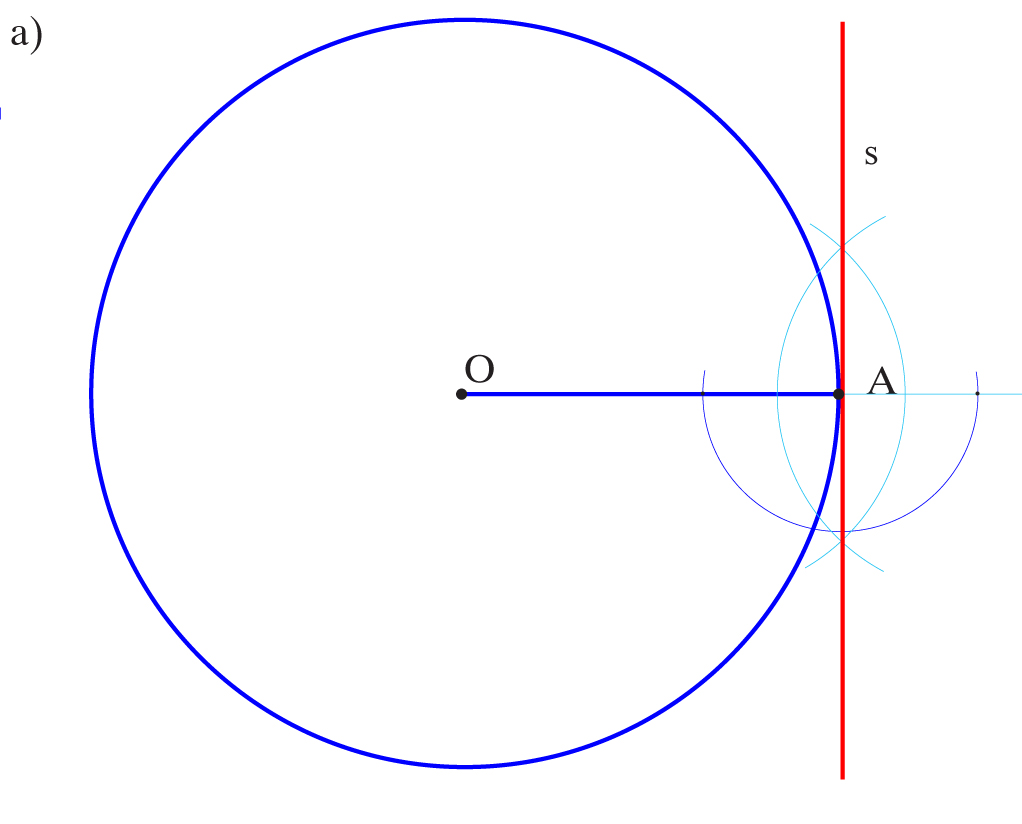
a)
W punkcie A wstawiamy prostopadłą do promienia OA otrzymując szukaną styczną s.
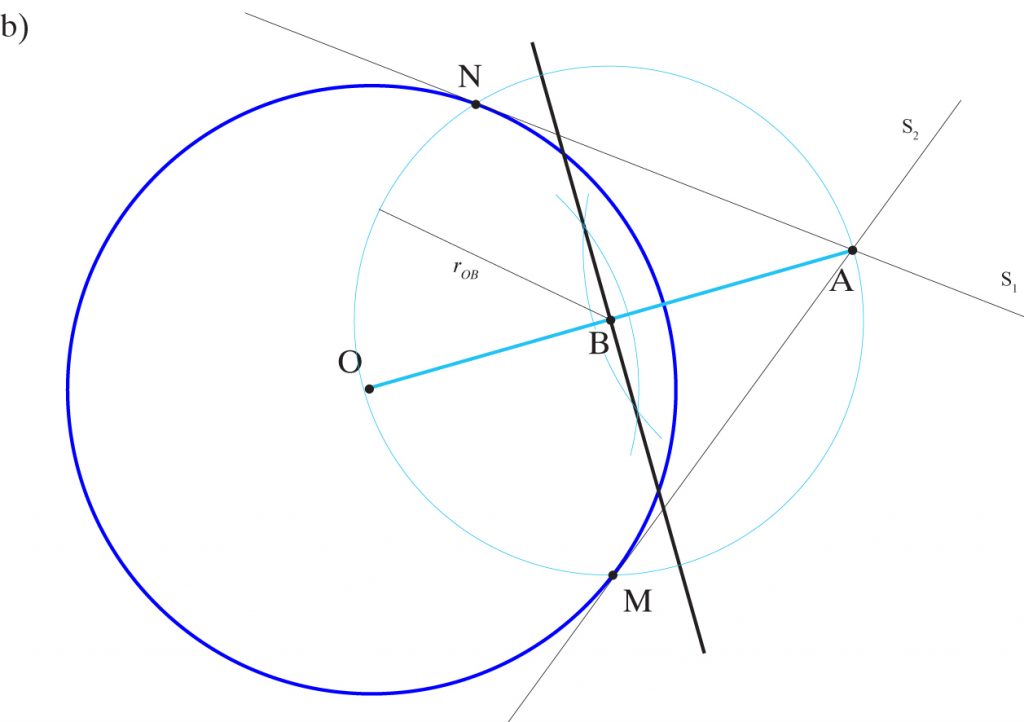
1. Łączę punkt O z punktem A. Otrzymuję odcinek OA.
2. Kreślę symetralną odcinka OA. Uzyskuję punkt B.
3. Kreślę okrąg o środku B i promieniu długości OB. Otrzymuję punkty N i M na przecięciu dwóch okręgów.
4. Prowadzę proste AM i AN styczne S1 i S2 do okręgu przechodzące przez punkt A.
Zadanie 9
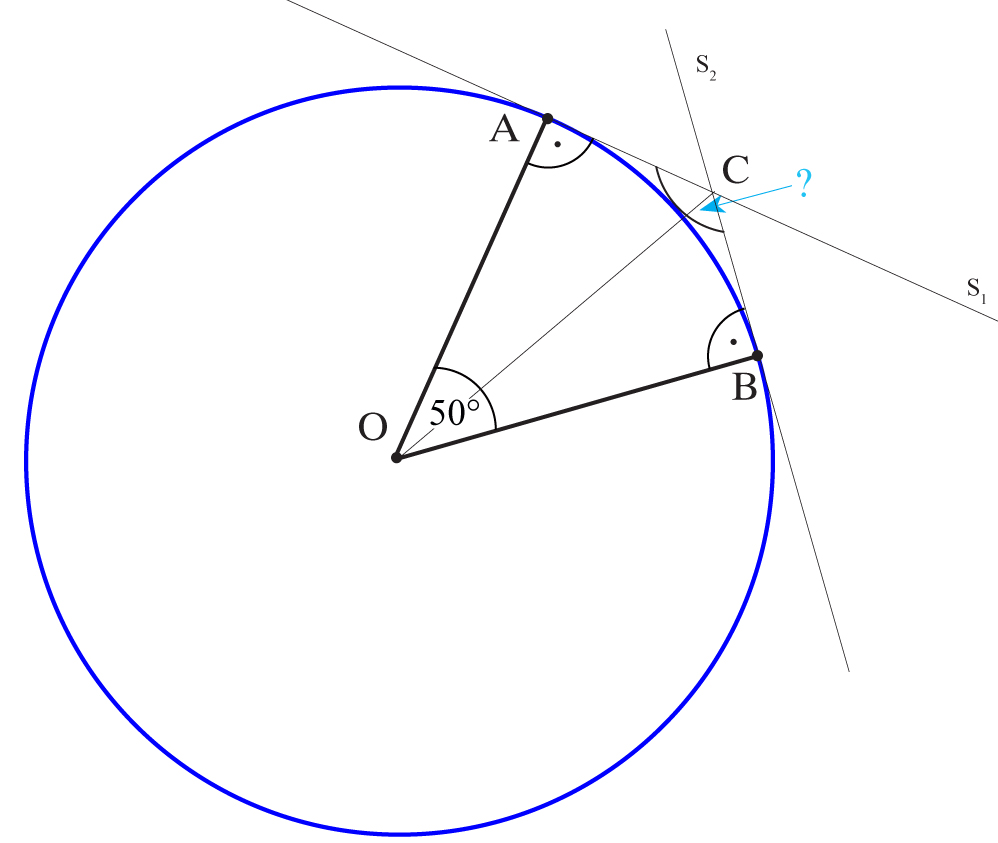
Dwa promienie tworzą kąt 50°. Ile stopni ma kąt, który tworzą styczne do okręgu w końcach tych promieni?
Rozwiązanie:
Kąt obc = kąt oac = 90°, jako kąt stycznej z promieniem.
Kąt acb = 360°- 2 . 90°-50°= 360°-230°=130°
Odpowiedź: Szukany kąt ma miarę 130°
Pamiętaj!
- Kąt, którego ramiona zawierają promienie okręgu (wierzchołek kąta pokrywa się ze środkiem okręgu) nazywamy kątem środkowym.
- Kąt wypukły, którego ramiona zawierają dwie cięciwy okręgu o wspólnym końcu, nazywa się kątem wpisanym w ten okrąg.
- Jeżeli kąt wpisany i kąt środkowy opierają się na tym samym łuku, to kąt środkowy jest dwa razy większy od kąta wpisanego.
- Jeśli kąt wpisany oparty jest na półokręgu (na średnicy), to jest on kątem prostym.
- Jeśli kąty wpisane oparte są na tym samym łuku, to są równe.
Zadanie 10:
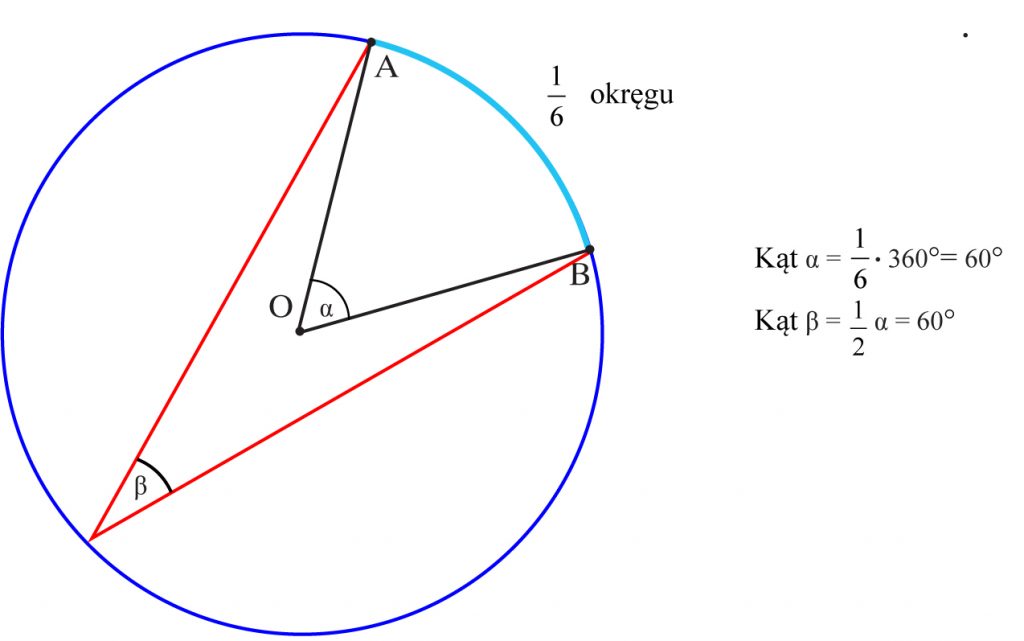
Oblicz miarę kąta wpisanego opartego na:
a) 1/6 okręgu
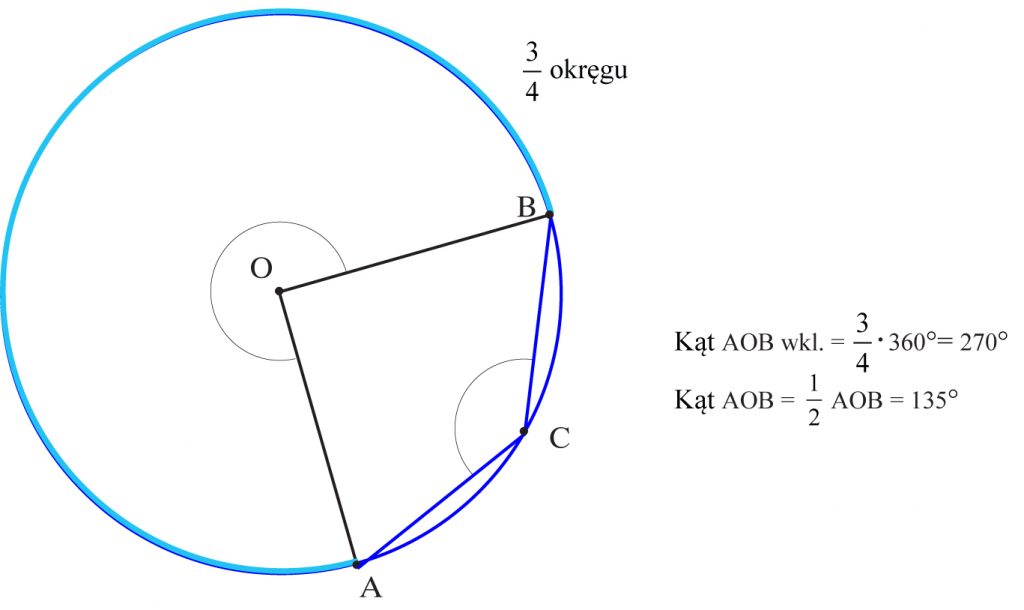
b) 3/4 okręgu
Zadanie 11
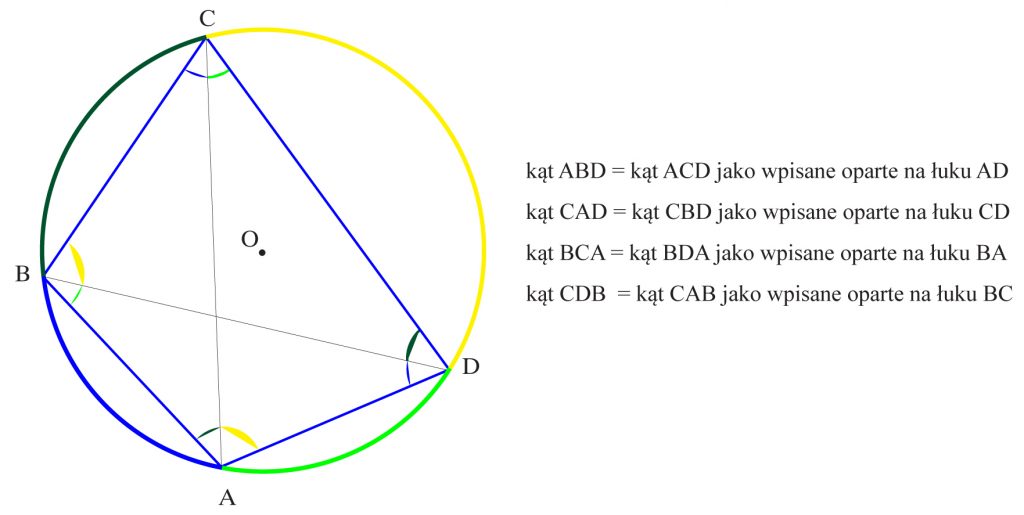
Wierzchołki czworokąta ABCD leżą na okręgu. Poprowadzono obie przekątne. Które kąty figury są równe i dlaczego?
Z kątami środkowymi związana jest konstrukcja niektórych wielokątów foremnych.
WIELOKĄT FOREMNY, to taki, którego wszystkie boki i kąty są równe.
Uwaga:
- Pośród trójkątów – wielokątem foremnym jest trójkąt równoboczny.
- Pośród czworokątów – wielokątem foremnym jest kwadrat.
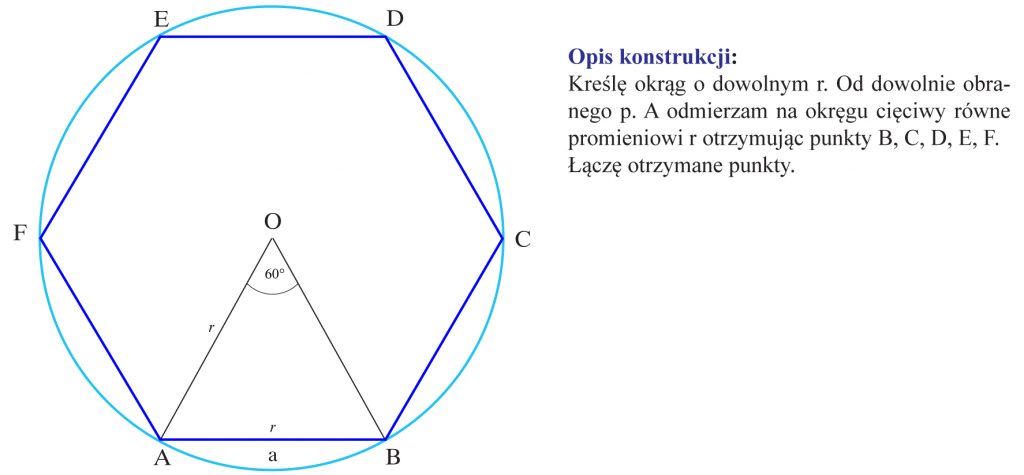
- Najłatwiej wykonać konstrukcję sześciokąta foremnego, ponieważ jego bok jest równy promieniowi okręgu opisanego na tym sześciokącie.
Uzasadnienie: kąt AOB = 360° = 60° . Ponieważ AO = OB = r, więc kąt OAB = kąt ABO = (180° – 60°) : 2 = 60°. Jest to więc trójkąt równoboczny, w którym AB = a = r.
Jeżeli w okręgu podzielonym na 6 równych łuków (konstrukcja sześciokąta) połączę odcinkami co drugi punkt otrzymam trójkąt równoboczny.
Zadanie 12
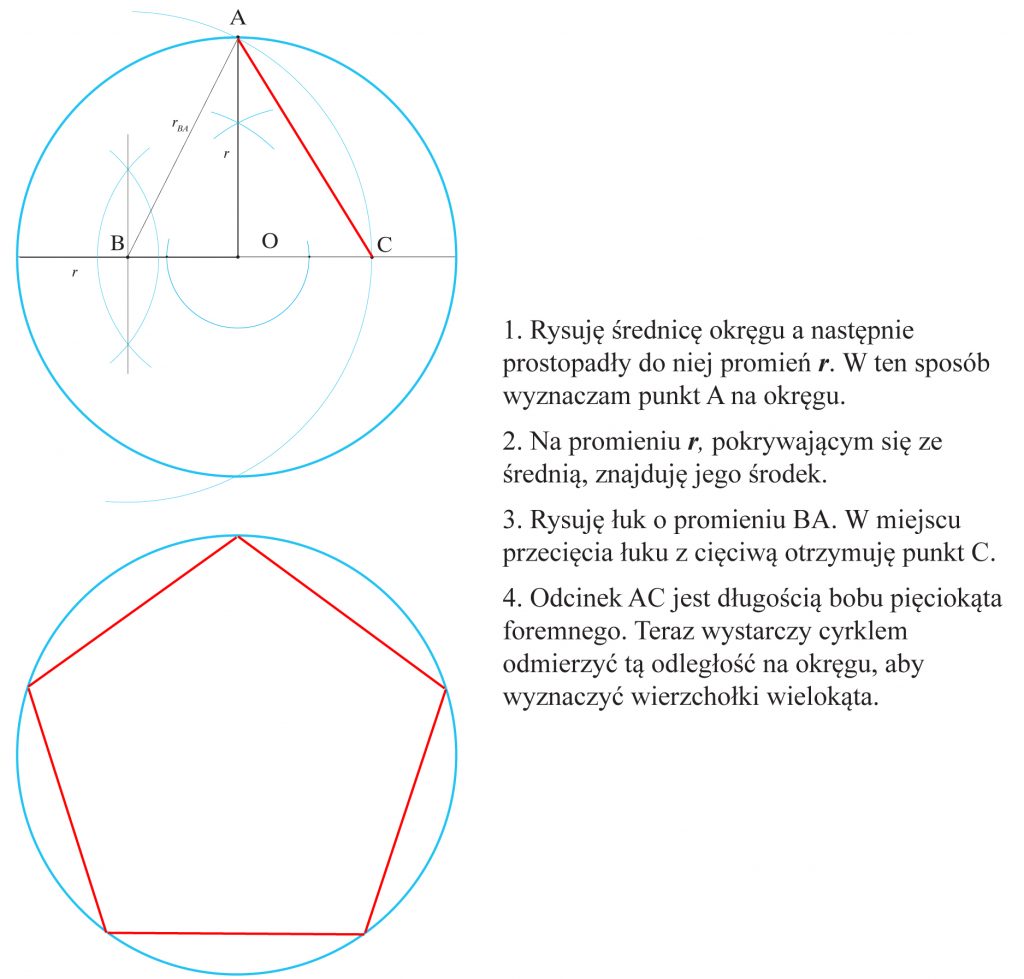
Wykreśl pięciokąt foremny.
Sposób 1
Obliczam kąt środkowy pięciokąta foremnego oparty na jego boku.
Kąt AOB = 360° : 5 = 72°
W okręgu kreślę kąt AOB = 72°. Rozwartością odcinka AB odmierzam na okręgu łuki BC, CD, DE i DA otrzymując punkty, które są wierzchołkami pięciokąta.
Sposób 2