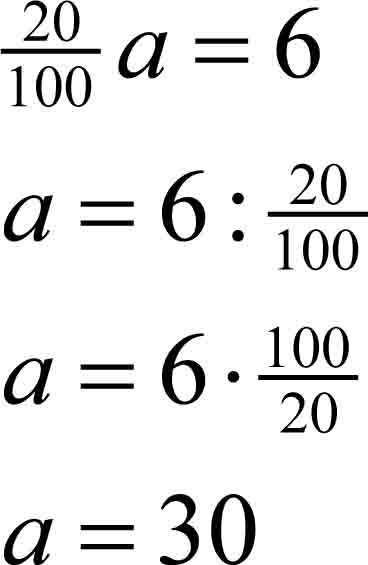Procent – co to jest?
Zapamiętaj! Procent to setna część całości.
Można napisać tak:
Znak procentu można zwyczajnie zastąpić ułamkiem . Na przykład: 15% ceny roweru, to 15· 1/100, czyli 15/100 ceny roweru.
Cztery klasyczne zadania
Każde zadanie związane z obliczeniami procentowymi sprowadza się do jednego z poniższych zagadnień. Jeśli nauczysz się tych schematów, Twoje kłopoty z procentami skończą się raz na zawsze.
1. Oblicz x% z liczby y.
Przykład: Wyznacz 6% liczby 150.
Zobacz, tak to trzeba rozwiązać:
Odpowiedź: 6% liczby 150 jest równe 9.
2. Ile procent liczby y stanowi liczba x?
Przykład: Jakim procentem liczby 40 jest liczba 5?
Rozwiązanie:
Odpowiedź: Liczba 5 stanowi 12,5% liczby 40.
3. x% jakiej liczby stanowi liczba y?
Przykład: 20% jakiej liczby wynosi 6?
Rozwiązanie: 20%a=6
Odpowiedź: 20% liczby 30 równa się 6.
4. Liczbę x zwiększono (lub zmniejszono) o y%. Jaką liczbę otrzymano?
Przykład: Cenę towaru wynoszącą 80 złotych podwyższono o 15%. Jaka była cena towaru po podwyżce?
Rozwiązanie: 15% liczby 80 jest równe 12 (15/100·80). Cena towaru (z osiemdziesięciu złotych) wzrosła więc o 12 złotych.
Odpowiedź: Po podwyżce towar kosztował 92 złote.
Uwaga! Gdyby cenę towaru obniżono o 15% (czyli w tym przypadku o 12 złotych), to cena po obniżce wynosiłaby 68 złotych (80 – 12).
Nie daj się złapać! Czytaj uważnie polecenia!
Pamiętaj, że procent nie działa w oderwaniu od całości. Dlatego na przykład 8% ceny a może być zupełnie inną liczbą niż 8% ceny b.
Zapamiętaj na przykładach!
Przykład 1.
Cenę towaru podwyższono o 15%, a następnie nową cenę podwyższono jeszcze o 10%. O ile procent wzrosła łącznie cena towaru?
Odpowiedź, że cena wzrosła łącznie o 25% (15+10), to odpowiedź BŁĘDNA! Dlaczego? Dlatego, że drugą podwyżkę naliczano od ceny już zwiększonej, a więc od innej, niż liczono pierwszą podwyżkę.
Załóżmy, że początkowa cena towaru wynosiła a złotych. Cena po podwyżce o 15% będzie więc wynosić a + 15%a, to jest 1,15a. Drugą podwyżkę (tę o 10%) trzeba więc naliczyć od nowej ceny:
1,15+10%·1,15a=1,15a+0,115a=1,265a
Cena po dwóch podwyżkach jest równa 1,265a. Łącznie cenę podstawową (a) zwiększono o 0,265a, czyli o26,5/100, to jest o 26,5% ceny pierwotnej.
Łączna podwyżka wynosiła więc 26,5%.
Przykład 2.
Pani Kołakowska założyła w banku lokatę w wysokości 4000 złotych. Oprocentowanie roczne wynosi 6%. Oblicz, jaka będzie wysokość kapitału pani Kołakowskiej po dwóch latach trwania lokaty.
Tutaj, podobnie jak poprzednio, najpierw musimy obliczyć wysokość kapitału pani Kołakowskiej po roku trwania lokaty. Sumę 4000 złotych zwiększamy więc o 6%.
6% · 4000=6/100 · 4000=240
Po roku bank doda do początkowego kapitału pani Kołakowskiej odsetki w wysokości 240 złotych. Stan lokaty po roku będzie więc równy 4240 złotych. Od tej ostatniej sumy zostaną naliczone odsetki w drugim roku. Zatem teraz zwiększamy o 6% tę nową sumę.
6% · 4240 = 6/100 · 4240 = 254,4
W drugim roku pani Kołakowska wzbogaci się o kwotę 254 zł 40 gr. Wprawdzie oprocentowanie jest wciąż jednakowe, ale w drugim roku odsetki naliczamy od wyższego kapitału.
Ostatecznie otrzymujemy:
Początkowy kapitał: 4000 zł
Odsetki w pierwszym roku: (6% z 4000 zł): 240 zł
Odsetki w drugim roku (6% z 4240 zł): 254,4 zł
Razem (wysokość kapitału po dwóch latach): 4494,4 zł
Na egzaminie spodziewaj się takich zadań:
Firma budowlana Super Tower-Bridge (STB) w roku 2000 zbudowała w Polsce łącznie 85 mostów, wiaduktów i estakad. Natomiast w roku 2001 STB zbudowała w Polsce kolejnych 100 takich obiektów. Liczba wykonanych w 2001 r. inwestycji wzrosła więc w stosunku do roku 2000 o:
A. 15%,
B. mniej niż 15%,
C. więcej niż 15%,
D. nie da się tego określić.
Liczba zbudowanych przez STB obiektów wzrosła z 85 do 100 sztuk (o 15 sztuk), ale jaki to procent? 15/85, to więcej niż 15/100, a więc więcej niż 15%. Zatem prawidłowa odpowiedź to C.
W teście matematyczno-przyrodniczym mogą pojawić się diagramy, a Ty będziesz musiał je prawidłowo zinterpretować! Dlatego przypominamy, jak odczytaćæ diagram kołowy!
Przykład
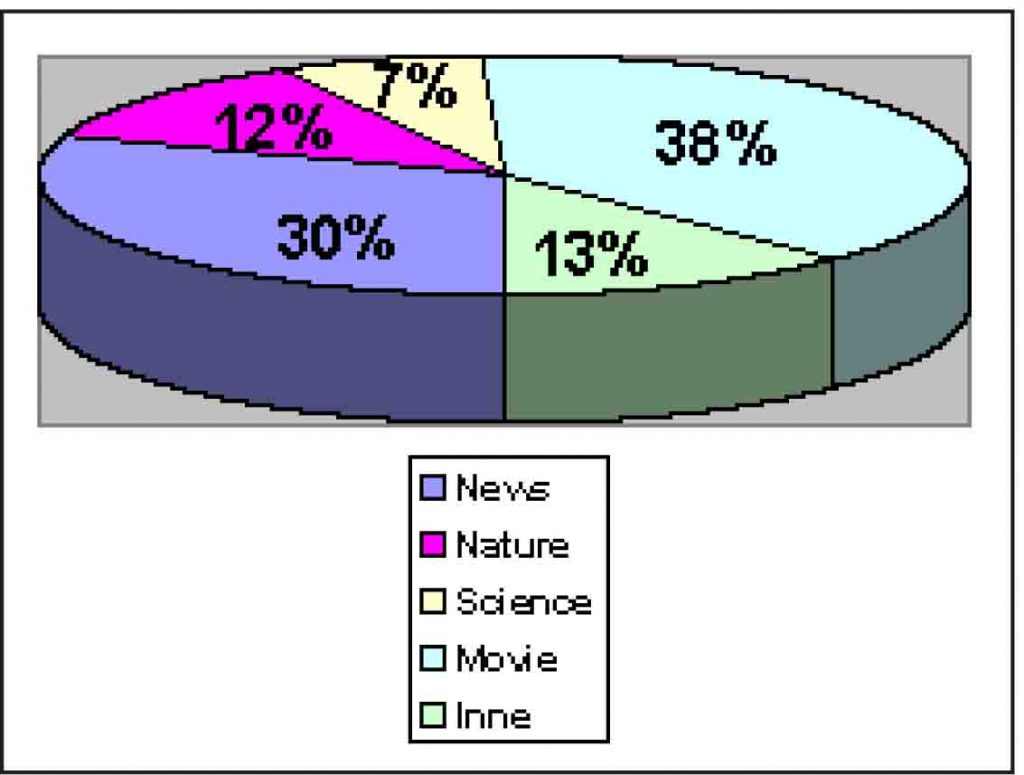
Na poniższym diagramie przedstawiono procentowy udział każdego z czterech największych kanałów telewizyjnych w dochodach z reklam w roku 2001.
Odpowiedz na następujące pytania:
A. Jaki (w procentach) udział w dochodach z reklam przypadł dwóm największym kanałom telewizyjnym?
B. Które kanały telewizyjne zdobyły dla siebie ponad 1/3 rynku?
C. Jaką sumę pieniędzy zarobił na reklamach kanał Science?
D. O ile więcej pieniędzy zarobił na reklamach kanał News od kanałów Nature i Science łącznie?
Teraz sprawdź, czy dobrze zrozumiałeś pytania:
A. Dwa największe kanały telewizyjne to oczywiście Movie (38%) i News (30%). Łączny udział tych dwóch stacji stanowi więc 68% całej puli dochodów z reklam telewizyjnych.
B. 1/3 całości to 33 1/3%. Ten pułap osiągnęła tylko jedna stacja – Movie (38%).
Zauważ, że diagram przedstawia tylko udział procentowy w zyskach. Nie możemy więc powiedzieć nic o sumach zarobionych przez poszczególne stacje telewizyjne. Gdyby na przykład pod diagramem była dodatkowa informacja: „Stacja News zarobiła (w roku 2001) na reklamach 42 miliony złotych”. Wtedy na pytania C. i D. również da się odpowiedzieć:
C. Stacja News miała 30% udział w rynku reklam. Jednocześnie zarobiła 42 mln złotych. Można więc obliczyć, że 1% udziału stanowi
1,4 mln złotych (42 mln : 30). Zatem 7% rynku, to mln, co z kolei jest równe 9,8 mln złotych. Tyle właśnie zarobił Science.
D. Nature i Science zdobyły łącznie 19% udziału, a to w przeliczeniu na gotówkę wynosi 19 · 1,4 mln złotych, to jest 26,6 mln złotych. News zarobił 42 miliony złotych, to znaczy — o 15,4 mln złotych więcej.
Zadanie
Basia i Ania mają kolekcje pocztówek. Basia przyniosła do szkoły 30% swoich pocztówek, a Ania 10% swoich. Okazało się, że obie dziewczynki przyniosły do szkoły po tyle samo pocztówek. Z tego wynika, że:
A. kolekcja Ani jest większa,
B. kolekcja Basi jest większa,
C. kolekcja jednej z dziewczynek jest większa o 20 pocztówek,
D. nie da się odpowiedzieć, która z dziewczynek dysponuje większą kolekcją pocztówek.
– A jak Ci się wydaje?
– Wydaje mi się, że odpowiedź B. jest prawidłowa. Basia przyniosła 30% pocztówek, a Ania 10%, czyli Basia ma ich więcej.
– Odpowiedź B. zdecydowanie nie jest prawidłowa! Zobacz, że 10% pocztówek Ani to tyle samo, co 30% pocztówek Basi! Kolekcja Ani jest więc większa, i to trzykrotnie!