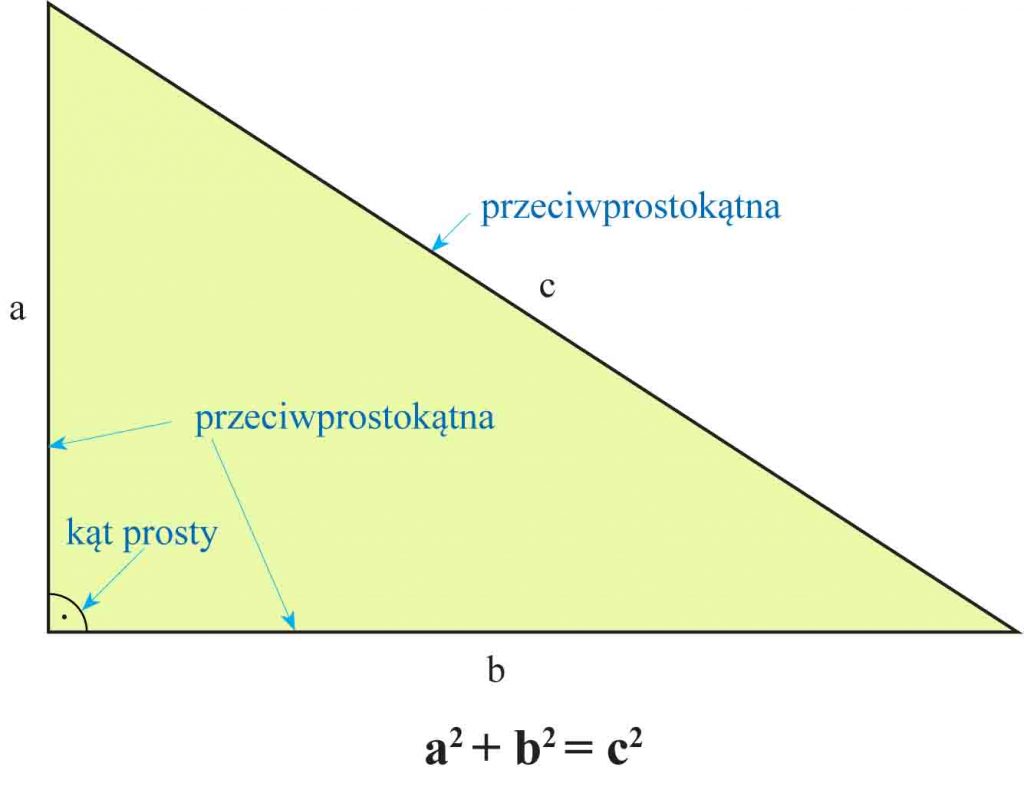
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
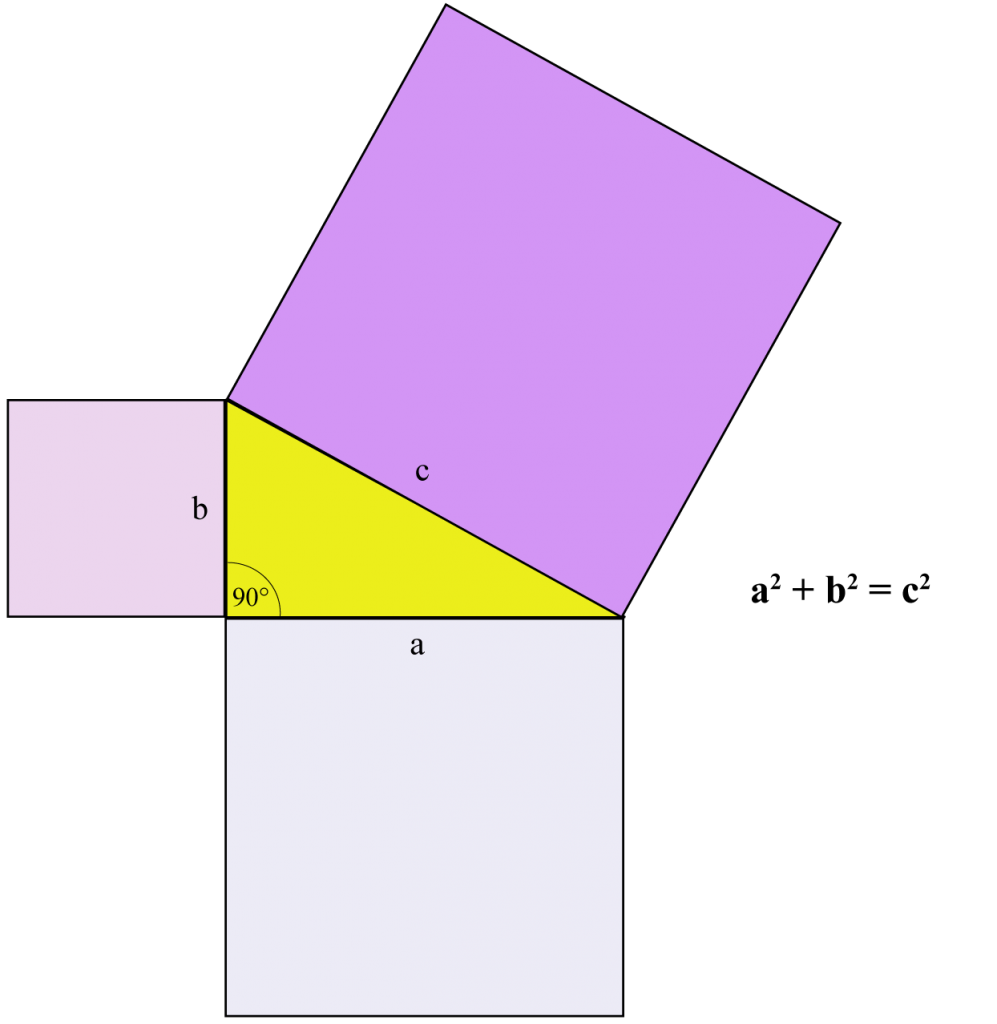
Twierdzenie Pitagorasa można również przedstawić tak:
Suma pól kwadratów A i B jest równa polu kwadratu C.
Jeśli wiesz, że trójkąt jest prostokątny, i znasz długość dwóch dowolnych jego boków, to możesz obliczyć długość boku trzeciego.
To jest ważne!
Wzór a² + b² = c² stosujemy tylko wtedy, gdy literami a, b oznaczone są długości przyprostokątnych, a literą c – długość przeciwprostokątnej trójkąta prostokątnego.
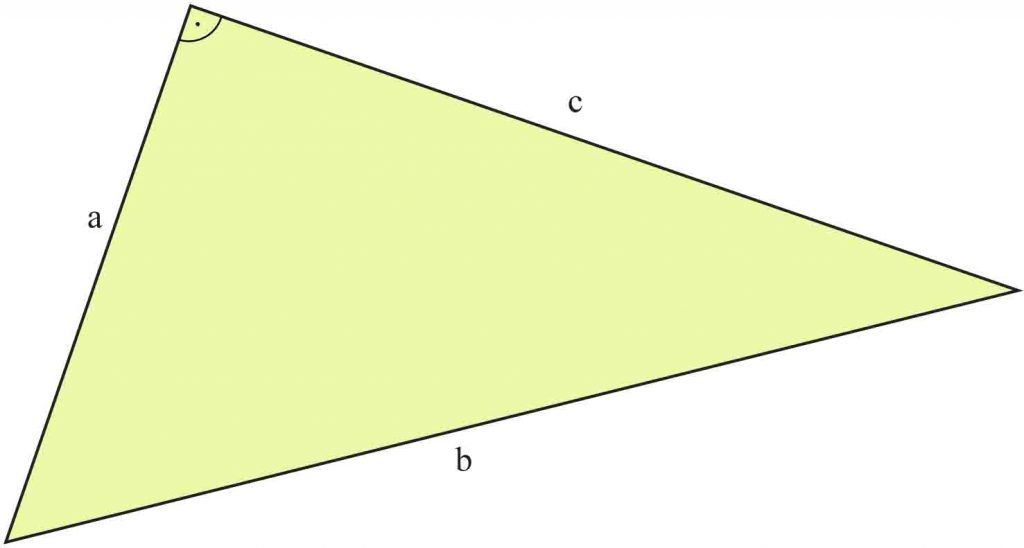
Gdy oznaczenia są inne, wtedy nie można automatycznie stosować tego zapisu. Na przykład:
W tym przypadku zachodzi zależność: a² + c² = b²
Twierdzenie odwrotne do twierdzenia Pitagorasa
Jeśli suma kwadratów długości dwóch krótszych boków pewnego trójkąta jest równa kwadratowi długości najdłuższego boku, to trójkąt ten jest prostokątny.
Przykład:
Sprawdź, czy trójkąty o podanych długościach boków są prostokątne:
a) p = 7, q = 24, r = 25
b) m = 2√2, n = 3, s = 1
c) x = 6, v = 14, u = 8
Jak to rozwiiązać?
To nic trudnego. Najpierw w każdym z przykładów należy ustalić, który bok jest najdłuższy.
- a) 7² + 24² = 49 + 576 = 625 = 25², czyli p² + q² = r², zatem trójkąt jest prostokątny.
- b) (2√2)² = 8, natomiast 3² = 9, zatem najdłuższy bok to ten o długości n. Sprawdzamy więc, że s² + m² = n² i w ten sposób rozstrzygamy, że trójkąt o bokach m, n, s również jest prostokątny.
- c) W tym przypadku najdłuższy bok to v. Otrzymujemy więc:
x² + u² = 36 + 64 = 100, natomiast v² = 144. Trójkąt ten nie jest więc prostokątny.
Takiego zadania spodziewaj się na teście!
Oblicz długość dłuższej przekątnej rombu o boku równym 25, którego krótsza przekątna wynosi 30.
Jak to rozwiązać?
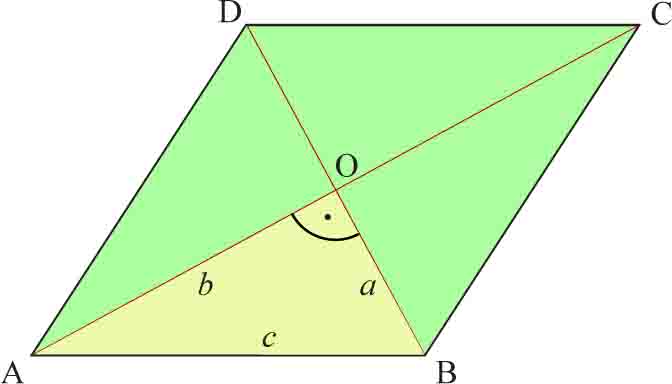
To jest zadanie z geometrii i dlatego najpierw sporządź rysunek pomocniczy!
Wiemy, że przekątne rombu przecinają się pod kątem prostym i dzielą się na połowy. Zatem: |AB| = 25, |OB| = 15 a trójkąt ABO jest prostokątny. Korzystając z twierdzenia Pitagorasa dla tego trójkąta prostokątnego, otrzymujemy więc długość odcinka AO.
a²+b²=c²
15² +b²=25²
b²=25²-15²=625-225=400
b=20
|AO| = 20. Dlatego dłuższa przekątna rombu (AC) ma długość 40.
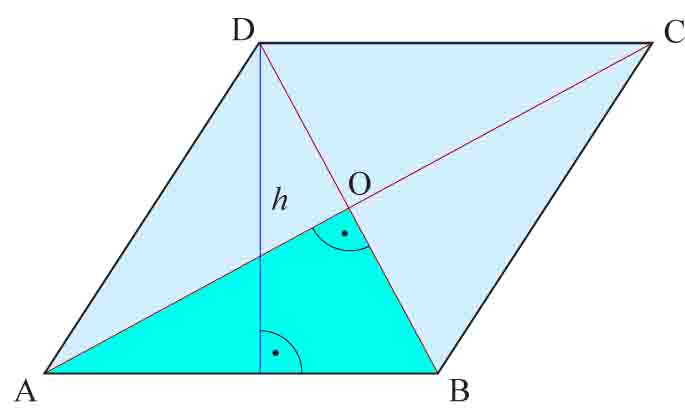
Zapamiętaj! Wysokość (trójkąta, rombu, równoległoboku) zawsze pada pod kątem prostym do podstawy.
To musisz umieć przed egzaminem:
Wzory na przekątną kwadratu i wysokość trójkąta równobocznego wynikają bezpośrednio z twierdzenia Pitagorasa.
Zadanie
Przekątne rombu mają długości równe 32 i 24. Oblicz wysokość rombu.
Najpierw należy naszkicować rysunek pomocniczy. Będzie on wyglądał tak:
Wiemy, że |AC| = 32, |BD| = 24.
Odcinki AO i BO mają odpowiednio długości 16 i 12. Skorzystamy więc z twierdzenia Pitagorasa dla trójkąta ABO.
16²+12²=|AB|²
|AB| = 20
Pole rombu równe jest
Inny wzór na pole rombu P= a·h
Mając długość podstawy i pole rombu możemy obliczyć jego wysokość
384 = 20·h
To h =384:20=19,2
Odpowiedź: h = 19,2.