Zadania na klasówkę!
Zadanie 1.
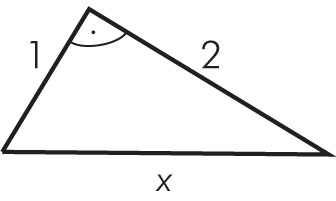
a) Przyprostokątne trójkąta prostokątnego mają długości 1 i 2. Oblicz długość przeciwprostokątnej tego trójkąta.
b) Jedna z przyprostokątnych trójkąta prostokątnego ma długość 7,5 cm, a długość przeciwprostokątnej wynosi 12,5 cm. Oblicz pole i obwód tego trójkąta.
Rozwiązanie: Wykonajmy rysunek zgodny z treścią zadań i ułóżmy twierdzenie Pitagorasa:
a)
x² = 1² + 2²
x² = 1 + 4
x = √5
Odpowiedź: Długość przeciwprostokątnej wynosi √5.
b)
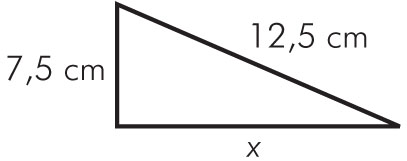
(7,5)² + x2 = (12,5)2
( )2 + x2 = ( )2
x2 = –
x2 = 100
x = 10 [cm]
Mając dane długości przyprostokątnych, można wyliczyć pole i obwód trójkąta:
P = · 10 cm · 7,5 cm = 37,5 cm2
L = 7,5 cm + 10 cm + 12,5 cm = 20 cm
Odpowiedź: Pole trójkąta wynosi 37,5 cm2, a obwód 20 cm.
Zadanie 2.
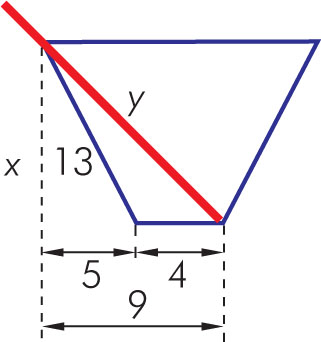
Jaką długość powinna mieć rurka włożona do szklanki, aby – przy takim ułożeniu jak na rysunku – wystawała ze szklanki na mniej więcej 3 cm? (Wymiary na rysunku podano w centymetrach).
Rozwiązanie: Wprowadzamy dodatkowe oznaczenia na rysunku:
Musimy dwukrotnie skorzystać z twierdzenia Pitagorasa: najpierw dla trójkąta prostokątnego o bokach x, 5 i 13.
x² + 5² = 13²
x² = 169 – 25
x = 12 [cm]
Teraz układamy twierdzenie Pitagorasa dla trójkąta prostokątnego o bokach x = 12, 9 i y.
y² = 12² + 9²
y² = 144 + 81
y = 15 [cm]
Ponieważ poza szklankę wystają 3 cm rurki, więc długość całej rurki wynosi 15 cm + 3 cm = 18 cm.
Odpowiedź: Rurka powinna mieć długość około 18 cm.
Zadanie 3.
Sprawdź, czy trójkąt o bokach 2, 4√2, 6 jest prostokątny.
Rozwiązanie: Stosujemy twierdzenie odwrotne do twierdzenia Pitagorasa. Ponieważ 2² = (4√2)² = 32, 62 = 36,
a 4 + 32 = 36, więc prawdziwa jest równość 22 + (4ö2)2 = 62.
Odpowiedź: Trójkąt o bokach 2, 4√2, 6 jest prostokątny.