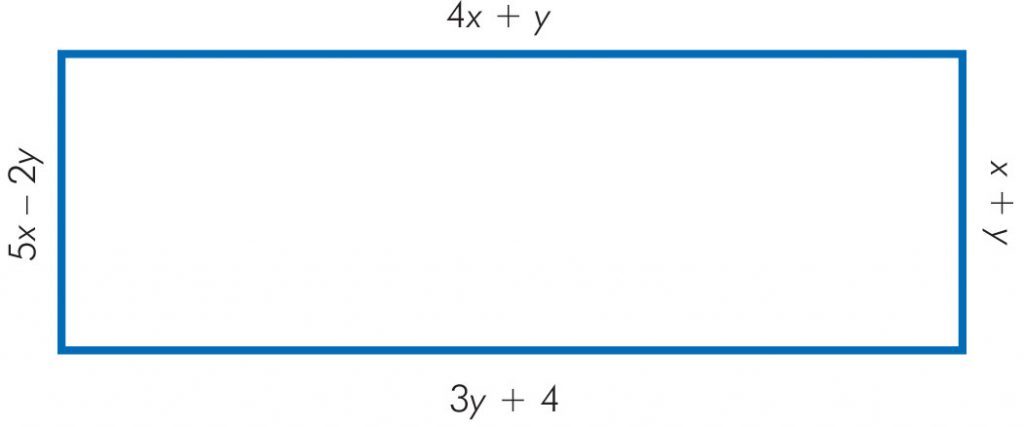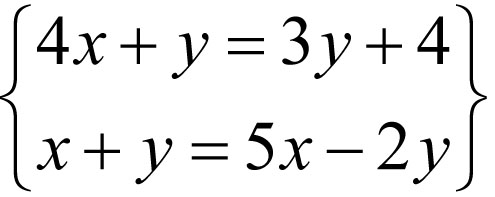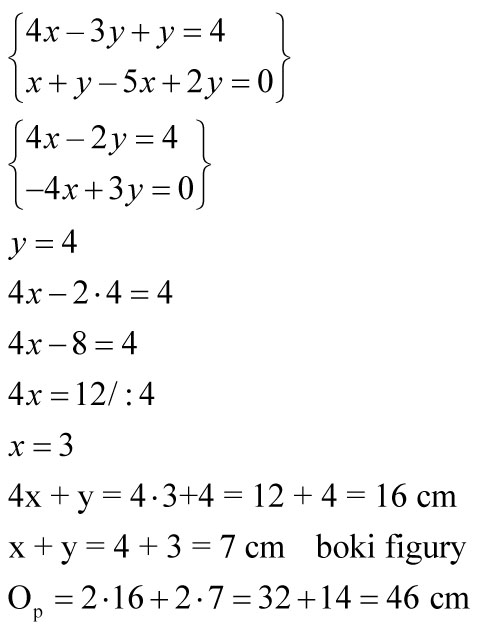Zadania na klasówkę!
Zadanie 1.
Narysuj 3 proste w taki sposób, by podzieliły one płaszczyznę na 6 części.
Rozwiązanie
Zadanie 2.
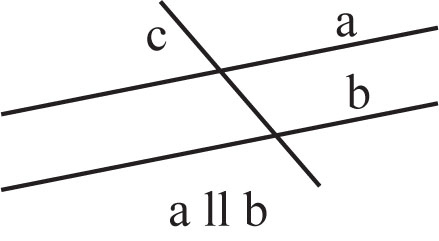
Oblicz miary kątów przyległych, jeśli wiadomo, że jeden z nich ma o 40° mniej od drugiego.
Rozwiązanie
Oznaczmy przez a miarę większego z kątów, wtedy a – 40° będzie oznaczało miarę mniejszego kąta.
Ponieważ suma kątów przyległych wynosi 180°, więc a + a – 40° = 180°. Po rozwiązaniu tego równania otrzymujemy, że a = 110°, a a – 40° = 70°.
Odpowiedź: Miary kątów przyległych wynoszą 110° i 70°.
Zadanie 3.
Czy istnieje trójkąt, którego miary kątów wynoszą:
a) 3,5°, 76,5°, 100°
b) 48°, 22°, 90°
Rozwiązanie
Wystarczy sprawdzić, ile wynosi suma miar tych kątów.
a) 3,5° + 76,5° + 100° = 180° – taki trójkąt istnieje
b) 48° + 22° + 90° = 160° – taki trójkąt nie istnieje
Zadanie na szóstkę!
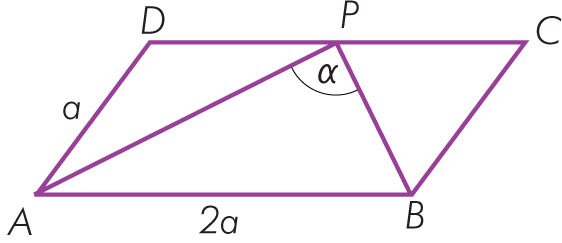
Punkt P jest środkiem boku narysowanego równoległoboku. Uzasadnij, że kąt α jest kątem prostym.
Rozwiązanie
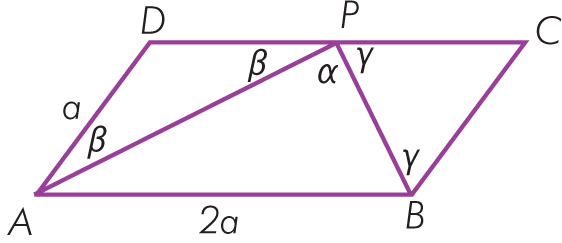
Z treści zadania wynika, że lDPl = lPCl = a. Trójkąty APD i BPC są więc równoramienne, czyli kąty przy podstawach są takie same. Wprowadźmy na rysunku oznaczenia:
W trójkącie ADP miara kąta ADP wynosi 180° – 2β, a w trójkącie BCP miarę kąta BCP można zapisać jako 180° – 2γ. Suma kątów 180° – 2b i 180° – 2γ wynosi 180°.
Mamy zatem:
180° – 2β + 180° – 2γ = 180°
–2β – 2γ = –180°
β + γ = 90°
Ponieważ α + β + γ = 180° oraz β + γ = 90°, więc α = 90°.
Pytanie z podręcznika
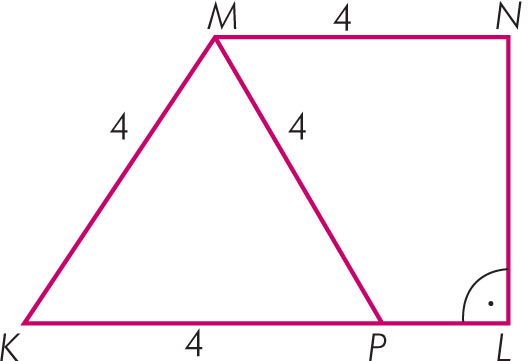
Jakie miary mają kąty narysowanego obok trapezu prostokątnego?
Rozwiązanie
Łatwo zauważyć, że trójkąt KPM jest równoboczny, czyli wszystkie jego kąty mają po 60°. Ponieważ w trapezie suma kątów leżących przy jednym ramieniu wynosi 180°, więc kąt KMN ma 120°. Kąt MNL jest oczywiście prosty.
Odpowiedź: Miary kątów trapezu wynoszą 60°, 120°, 90°, 90°.
Zadanie 4.
Oblicz obwód prostokąta przedstawionego na rysunku. Jeżeli przyjmiemy, że długość boków wyrażona jest w centymetrach, to czy wystarczy pół metra listewki, aby wykonać ten prostokąt?
Rozwiązanie:
Ponieważ odpowiednie boki są równe, układamy układ równań:
Rozwiązując ten układ równań, możemy dowiedzieć się, jaką długość mają boki tego prostokąta. Wiemy, że jednostką miary jest centymetr.
Odpowiedź: Obwód prostokąta wynosi 46 cm, więc pół metra listewki wystarczy, aby wykonać ten prostokąt.