Zapamiętaj!
Bryłami obrotowymi nazywamy bryły powstałe w wyniku obrotu pewnej figury płaskiej wokół prostej zwanej osią obrotu.
Zapamiętaj!
Walcem nazywamy figurę przestrzenną powstałą przez obrót prostokąta wokół prostej zawierającej jeden z boków prostokąta.
Uwaga!
Przekrojem osiowym bryły obrotowej nazywamy przekrój płaszczyzną zawierającą oś obrotu, a przekrojem poprzecznym nazywamy przekrój płaszczyzną prostopadłą do osi obrotu bryły.
Zadanie 1.
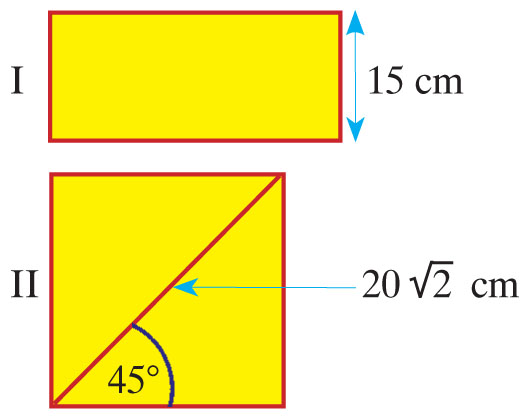
Rysunki przedstawiają rozwinięcia powierzchni bocznych walców. Który z walców ma dłuższy promień podstawy, jeżeli pole powierzchni całkowitej pierwszego z nich wynosi 360 cm², a jego wysokość ma 15 cm?
Rozwiązanie:
Obliczamy promienie obu walców:
I Ponieważ Pb = 360 cm², h = 15 cm,
po podstawieniu do wzoru otrzymujemy:
![]()
![]()
II Powierzchnia boczna tego walca jest kwadratem. Korzystając ze wzoru na przekątną kwadratu, wyliczamy, że długość boku kwadratu wynosi 20 cm. Zatem wysokość walca ma 20 cm i obwód podstawy walca ma 20 cm. Stąd wynika, że .
Odpowiedź: Dłuższy promień podstawy ma walec pierwszy.
Zadanie 2.
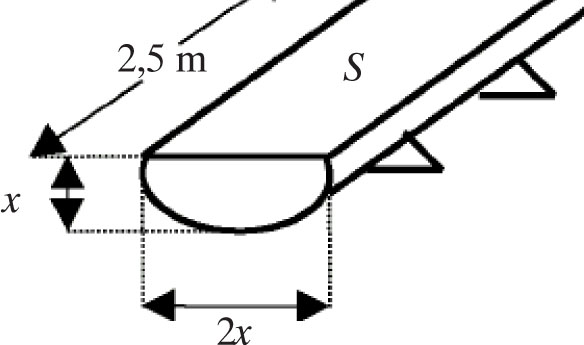
Na parkingu leśnym stoi ławeczka o długości 2,5 m wykonana z pnia drzewa w kształcie walca o obwodzie 3π dm, który przecięto płaszczyzną zawierającą przekrój osiowy. Oblicz pole powierzchni S tego przekroju.
Rozwiązanie:
Korzystamy ze wzoru na obwód koła:
2πr = 3π
r = 1,5 [dm]
Ponieważ r = x, więc boki prostokąta będącego przekrojem osiowym mają długości 3 dm i 2,5 m.
Stąd S = 0,3 m · 2,5 m = 0,75 m².
Odpowiedź: Pole powierzchni przekroju wynosi 0,75 m².
Zadanie 3.
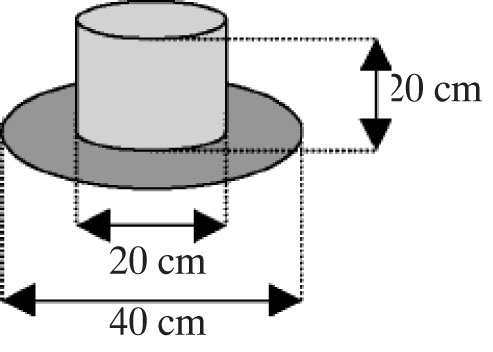
Na bal karnawałowy w przedszkolu mały Mateusz postanowił przebrać się za Zorro. Babcia zrobiła mu ze sztywnego papieru kapelusz. Ile materiału zużyła na jego wykonanie? Zużycie papieru jest większe o 6% ze względu na zakładki potrzebne do sklejenia kapelusza.
Rozwiązanie:
I sposób: Ilość zużytego na kapelusz papieru bez zakładek obliczymy, sumując pole koła o promieniu 20 cm i pole powierzchni bocznej walca o promieniu 10 cm i wysokości 20 cm:
P = π · 20² + 2π · 10 · 20 = 400π + 400πp =800π [cm²]
II sposób: Pole powierzchni kapelusza bez zakładek można też obliczyć jako sumę pola koła o promieniu 10 cm, pola powierzchni bocznej walca i pola pierścienia kołowego:
P1 = π · 10² = 100π
P2 = 2π · 10 · 20 = 400π
P3 = π · 20² – π · 10² = 300π
P = 100π + 400π + 300π = 800π [cm²]
Doliczamy teraz 6% na zakładki – ostatecznie otrzymujemy:
Pkapelusza = 800π + 0,06 · 800π = 848π [cm²]
Odpowiedź: Na wykonanie kapelusza babcia zużyła 848π cm² papieru.
Zadanie 4.
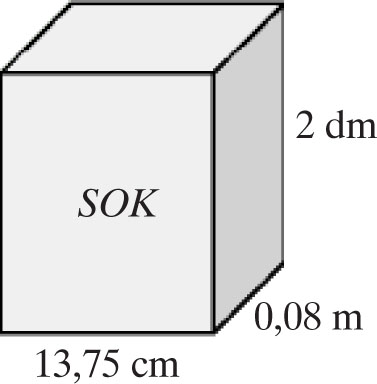
Do ilu szklanek w kształcie walca o wysokości 10 cm i promieniu podstawy 3 cm można wlać sok zawarty w prostopadłościennym kartoniku, jeżeli w szklankach sok sięga do 7/9 ich wysokości? Przyjmij za π≈22/7 .
Rozwiązanie
Najpierw obliczamy objętość soku zawartego w prostopadłościennym pudełku:
V1 = 13,75 cm · 8 cm · 20 cm = 2200 cm³.
Objętość soku znajdującego się w jednej szklance wynosi:
V2 = · p · 32 · 10 » · · 9 · 10 » 220 [cm³]
Aby udzielić odpowiedzi na zadane pytanie, wykonujemy dzielenie 2200 : 220 = 10.
Odpowiedź: Sok zawarty w kartoniku można wlać do 10 szklanek.