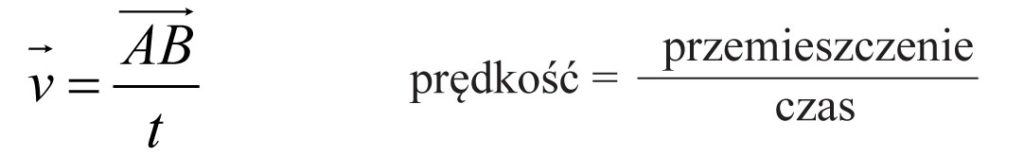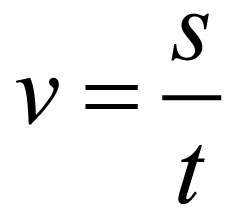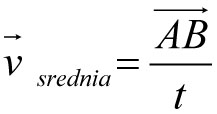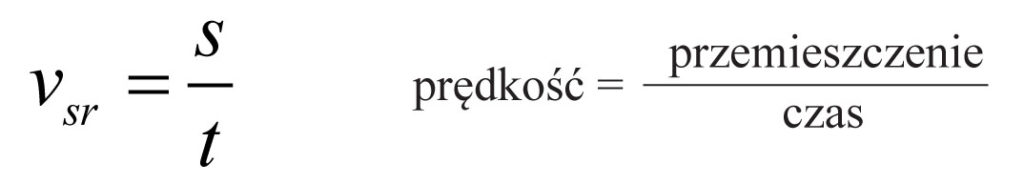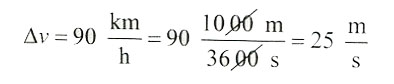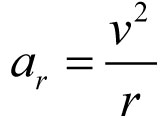1. Czym jest ruch?
Ruch jest zmianą położenia jednego ciała względem jakiegoś innego ciała. To proste, ale zapamiętaj, że zmiana ta zachodzi wraz z upływem czasu. To wybrane ciało, względem którego obserwujemy zmiany położenia innego ciała w przestrzeni, nazywamy układem odniesienia.
2. Jaka jest różnica między torem, drogą a przemieszczeniem ciała?
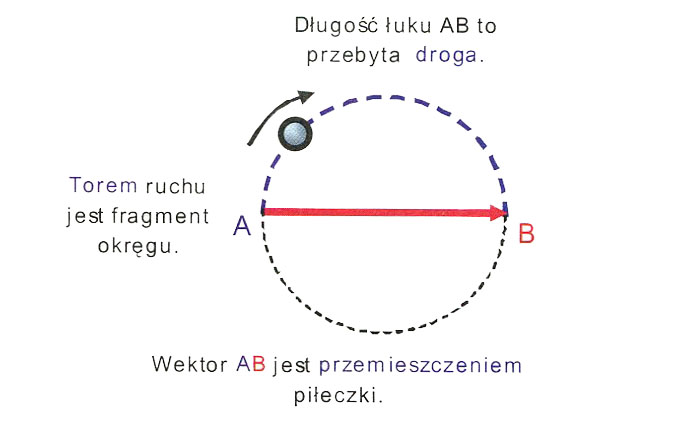
Torem ruchu jest linia, jaką zakreśla w przestrzeni poruszające się ciało. Droga to długość tego odcinka toru, który ciało przebyło w określonym czasie. Przemieszczenie to wektor, który łączy ze sobą początkowe i końcowe położenie ciała.
Skojarz na przykładzie!
Piłeczka porusza się po okręgu. Śledzimy jej ruch od punktu A do punktu B. Co jest w tym przypadku torem, co drogą, a co przemieszczeniem piłeczki?
3. Czym jest prędkość ciała?
Mówiąc o prędkości zwykle mówimy o prędkości chwilowej, czyli prędkości mierzonej w bardzo krótkim czasie. Tak rozumiana prędkość (v) to stosunek wektora przemieszczenia (czyli AB) do czasu (czyli t), w którym to przemieszczenie nastąpiło. Zapisujemy to tak:
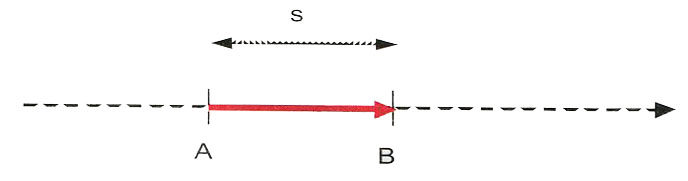
W ruchu po linii prostej wartość wektora przemieszczenia jest tym samym co długość przebytej drogi (s).
Wtedy możemy zapisać, że wartość prędkości jest równa:
Tak obliczoną wartość prędkości nazywamy również szybkością ciała.
Skojarz na przykładzie!
Podczas jazdy samochodem możemy obserwować na tzw. szybkościomierzu, jak zmienia się wartość prędkości chwilowej w każdej kolejnej sekundzie ruchu. Jeśli przez pewien czas szybkościomierz pokazuje stałą wartość, to poruszamy się ruchem jednostajnym. Każda zmiana wskazań wskazówki lub wyświetlacza oznacza, że jedziemy ruchem zmiennym.
4. Jak obliczać prędkość i szybkość średnią?
Wyraz „średnia” wskazuje na to, że bierzemy pod uwagę długi odcinek czasu. Prędkością średnią będzie więc stosunek wektora całkowitego przemieszczenia ciała do całego czasu trwania ruchu.
Najczęściej interesuje nas jednak długość przebytej drogi w określonym czasie, a nie całkowite przemieszczenie ciała. Posługujemy się wówczas szybkością średnią (potocznie też nazywaną prędkością). Obliczenie szybkości średniej (vśr) wymaga podzielenia całej przebytej drogi (czyli s) przez cały czas, jaki był potrzebny do jej przebycia (czyli t):
Skojarz na przykładzie!
Jeśli przejechaliśmy 300 kilometrów i zajęło nam to 5 godzin, to średnia szybkość wynosi:
Ta wartość nie mówi nam wiele o szczegółach podróży. Z taką szybkością mogliśmy bowiem jechać tylko przez kilka chwil. Przez resztę czasu szybkościomierz mógł pokazywać wartości większe lub mniejsze od 60 km/h.
5. Czym jest przyspieszenie?
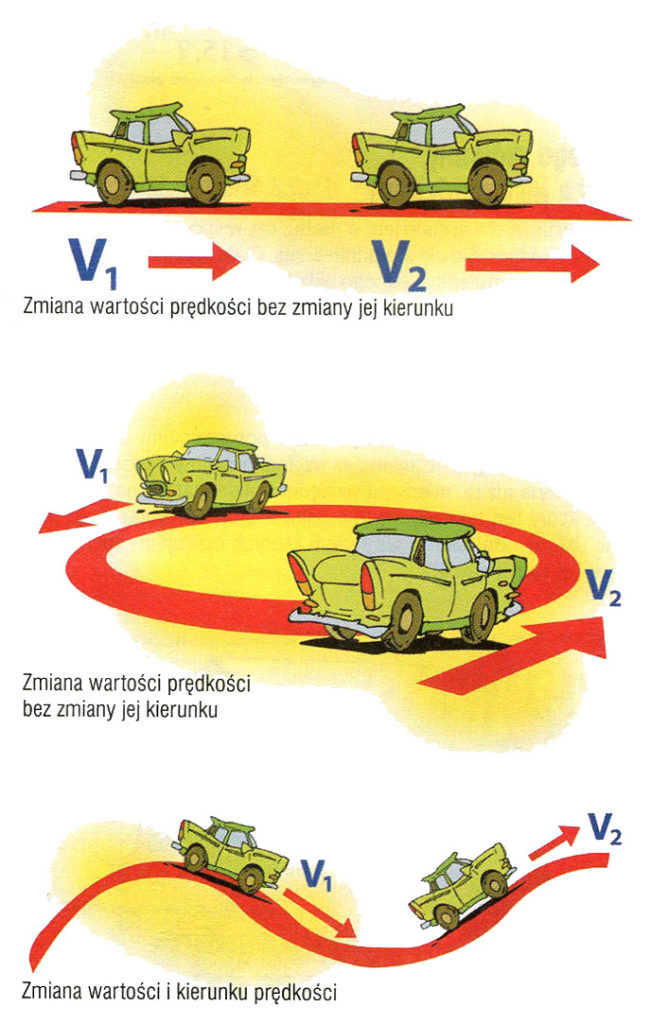
Z pojęciem przyspieszenia spotykasz się codziennie, gdy jadąc samochodem lub autobusem, doznajesz zmian prędkości. Przyspieszenie określa właśnie zmiany prędkości. Zmiana wektora prędkości oznaczać może zmianę jego wartości lub zmianę jego kierunku i zwrotu (lub też obu tych elementów jednocześnie). W fizyce wszelkie zmiany wielkości fizycznych zapisujemy przy użyciu greckiej litery Δ (delta).
6. Jak obliczamy przyspieszenie?
Przyspieszenie (czyli 
) informuje nas, jak zmienia się wektor prędkości ciała (czyli Δv) w miarę upływu czasu (czyli Δt).
Jeśli w chwili t1 ciało miało prędkość 
, a w następującej po niej chwili t2 ma już prędkość 
, to różnica wektorów prędkości też jest wektorem, stąd zapis: . Zmiana wektora prędkości nastąpiła w czasie: t2 – t1 = Dt, stąd zapis:
Jeśli wektor prędkości zmienia się zawsze tak samo, czyli zmienia się proporcjonalnie do czasu, to mówimy, że ciało przyspiesza jednostajnie. Wtedy wartość przyspieszenia jest stała.
Skojarz na przykładzie!
Jakie jest przyspieszenie samochodu, który ruszając z miejsca, na prostoliniowym odcinku jezdni, po 10 sekundach od startu osiągnął prędkość o wartości 90 km/h?
Zmiana prędkości wynosi: Δv = 90 km/h – 0 km/h = 90 km/h
Ta wielkość wyrażona w jednostkach podstawowych to:
Zmiana prędkości odbyła się w ciągu: t = 10 s
Szukane przyspieszenie to:
:
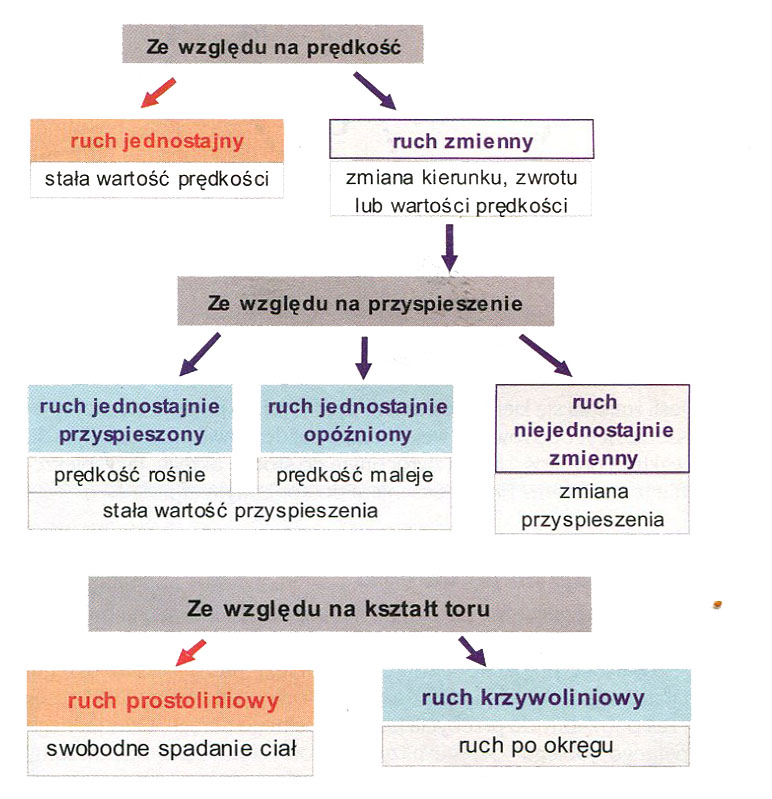
7. Jak dzielimy ruchy?
Ruchy można podzielić ze względu na to, jaki jest kształt toru ruchu i w jaki sposób zmienia się prędkość podczas ruchu.
8. Czym różni się ruch jednostajny od ruchu zmiennego?
W ruchu jednostajnym wartość prędkości nie ulega zmianie. Ruch zmienny to taki, w którym zmienia się prędkość ciała. Ponieważ prędkość jest wektorem, więc zmiana prędkości oznacza zmianę wartości lub zmianę kierunku i zwrotu tego wektora. Zmiana prędkości zawsze jednak oznacza… przyspieszenie. Ruch zmienny więc, to ruch z przyspieszeniem. Jeśli prędkość zmienia się proporcjonalnie do czasu ruchu, to taki ruch jest zmienny jednostajnie. Może on być jednostajnie przyspieszony lub jednostajnie opóźniony, zależnie od tego, czy prędkość rośnie, czy maleje.
9. Czym różni się ruch jednostajny prostoliniowy od ruchu jednostajnego po okręgu?
Oba te ruchy są jednostajne, co oznacza, że ich wartość prędkości nie ulega zmianie. Ruchy te różnią się, oczywiście, kształtem toru. Ale inny tor oznacza też inne położenie wektora prędkości.
Wektor prędkości ciała, poruszającego się po linii prostej, ma w każdej chwili kierunek zgodny z kierunkiem przemieszczania się ciała.
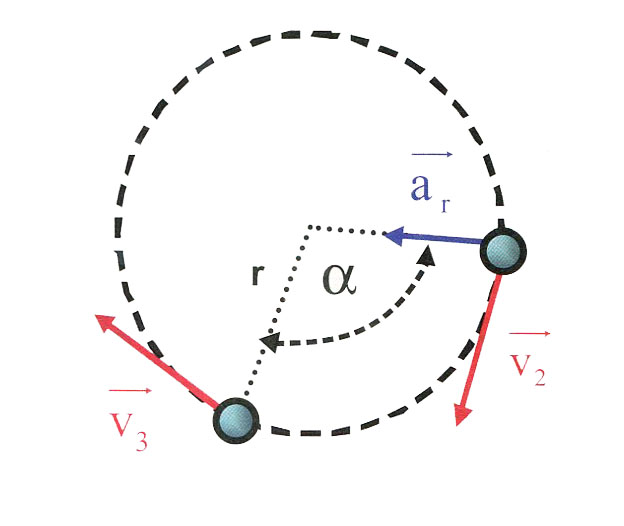
Dla ciała poruszającego się po okręgu, wektor prędkości jest w każdym momencie styczny do toru ruchu.
Jeśli zmienia się kierunek wektora prędkości, to pojawia się przyspieszenie. Jest ono również wektorem, w każdej chwili prostopadłym do wektora prędkości ciała i zwróconym do środka okręgu. Przyspieszenie to nazywamy przyspieszeniem dośrodkowym (ar).
10. Jak obliczyć prędkość i przyspieszenie w ruchu jednostajnym po okręgu?
Ciało poruszające się po okręgu ma prędkość liniową (v) i prędkość kątową (ω).
Wartość prędkości liniowej (v) dotyczy ruchu wzdłuż okręgu. Obliczamy ją, dzieląc całą drogę, czyli długość okręgu (2pr) przez czas potrzebny do przebycia jednego pełnego okręgu. Czas jednego pełnego „obiegu” okręgu nazywamy okresem ruchu i oznaczamy literą T. Wartość prędkości liniowej w ruchu jednostajnym po okręgu jest więc równa:
Jeśli ciało przemieszcza się po okręgu, to promień łączący środek tego okręgu z chwilowym położeniem ciała zakreśla w każdym momencie kąt (a). Wielkość tego kąta przez czas, w którym został zakreślony, to prędkość kątowa ciała (v). Ponieważ kąt pełny jest równy 2p, a czas pełnego obrotu to T, więc wartość prędkości kątowej możemy wyrazić następująco:
Z porównania wzorów łatwo zauważyć, że zachodzi zależność:
v = v · r
Przyspieszenie dośrodkowe w tym ruchu zależy od prędkości liniowej ciała i promienia okręgu i jest równe:
Skojarz na przykładzie!
Kolarz wykonał 12 okrążeń kołowego toru w czasie 4 minut. Jaka była wartość jego średniej prędkości liniowej, jeśli wiadomo, że promień toru wynosił 50 m?
Przebyta droga: s = 12 · 2π · r = 12 · 2π · 50 m = 1200π m
Czas przebycia drogi: t = 4 min = 4 · 60 s = 240 s
Wartość prędkości liniowej kolarza to:
11. Dlaczego mówimy,że ruch jest względny?
To, czy w danej chwili ciało jest w ruchu, czy w spoczynku, zależy wyłącznie od wybranego układu odniesienia. Ciało może być w tej samej chwili w ruchu, względem jednego układu odniesienia, i jednocześnie w spoczynku względem innego układu. Nie istnieje więc żaden wyróżniony układ, względem którego należy opisywać ruch.
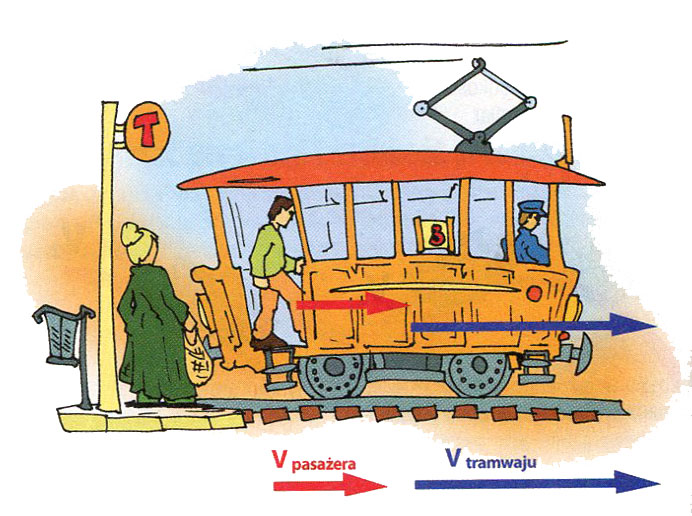
Skojarz na przykładzie!
Opisujemy ruch pasażera, który idzie w poruszającym się wagonie tramwaju. Jego prędkość, mierzona względem ściany wagonu (vp), jest zupełnie inna niż ta, mierzona względem obserwatora na przystanku (vs), który ten tramwaj właśnie mija. Wagon i przystanek to dwa różne układy odniesienia, względem których opisujemy ruch pasażera w tej samej chwili.
12. W jaki sposób dodajemy prędkości?
Bardzo często zdarza się tak, że ruch ciała jest wynikiem złożenia kilku ruchów zachodzących z różnymi prędkościami. Prędkość poruszającego się ciała jest wtedy wypadkową prędkości składowych.
Skojarz na przykładzie!
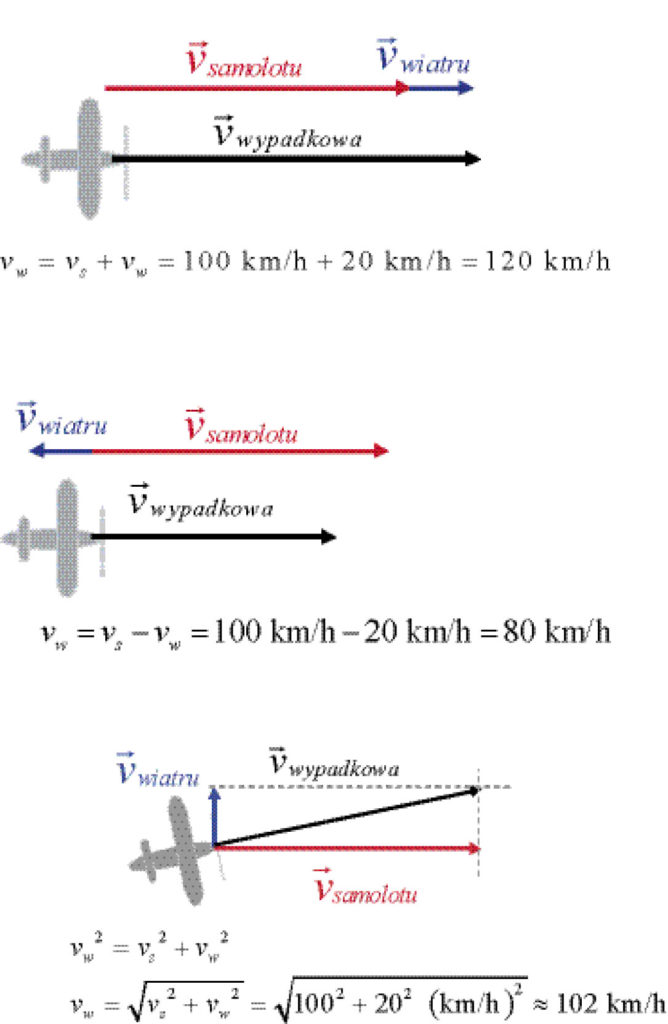
Sportowy samolot leci na wschód z prędkością 100 km/h. Znajdź jego prędkość względem ziemi, jeśli wiatr wieje w kierunku wschodnim z prędkością 20 km/h. Jak zmieni się sytuacja, gdy wiatr będzie wiał w kierunku zachodnim i północnym?
Problem ten rozwiązujemy graficznie, znajdując wypadkową dwóch różnych wektorów prędkości. Następnie obliczamy wartość liczbową prędkości wypadkowej. Na rysunkach obrano skalę długości wektorów w ten sposób, że 1 cm odpowiada prędkości 20 km/h. Zwróć uwagę, że dla dwóch wektorów prostopadłych do siebie znajdujemy długość wektora wypadkowego, korzystając z twierdzenia Pitagorasa!
W każdym z podanych przypadków prędkość wypadkowa samolotu względem ziemi jest inna, chociaż prędkość własna samolotu cały czas ma wartość 100 km/h.
