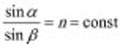Na teście matematyczno-przyrodniczym spodziewaj się takiego zadania!
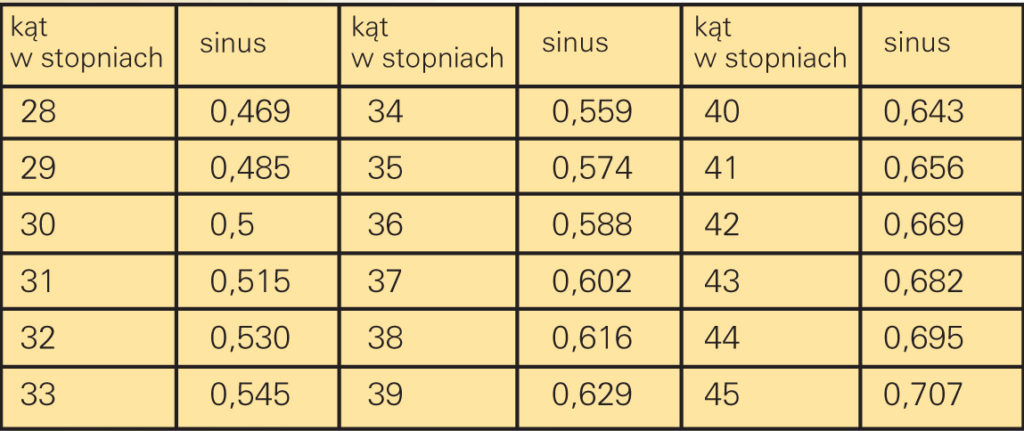
Oblicz kąt załamania światła w pewnym gatunku szkła, jeśli współczynnik załamania wynosi 1,4, a kąt padania jest równy 45o. Skorzystaj
z fragmentu tablic trygonometrycznych.
Jak to rozwiązać?
Najpierw przypomnij sobie niezbędne wiadomości. Na początek: prawo załamania światła. W ramce znajdziesz podstawowe informacje o funkcji sinus.
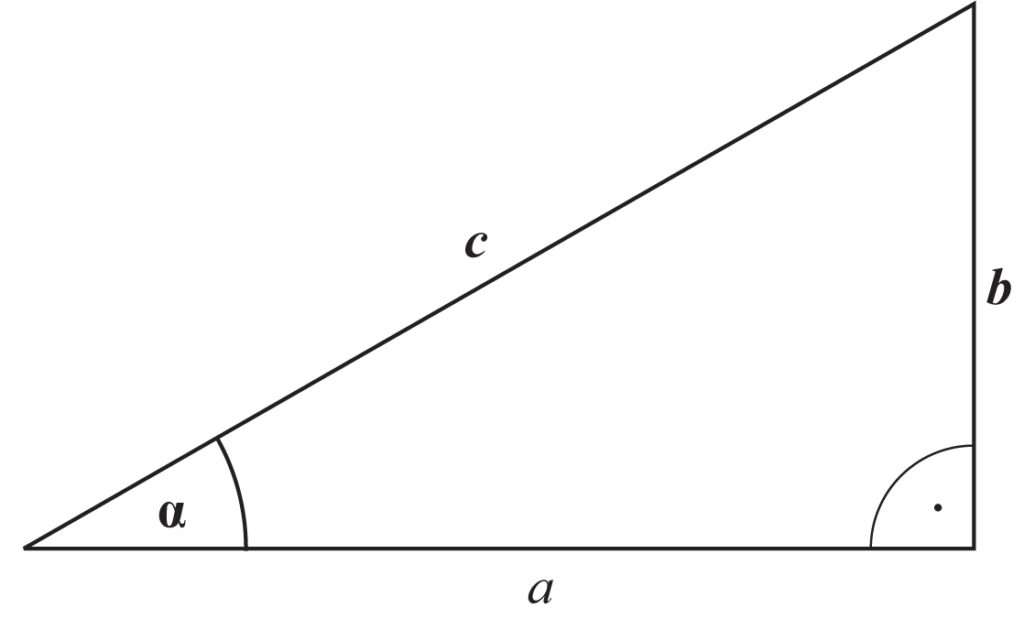
Sinus jest jedną z funkcji trygonometrycznych. Sinusem kąta ostrego w trójkącie prostokątnym nazywamy iloraz przyprostokątnej leżącej naprzeciwko kąta i przeciwprostokątnej.
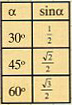
Wartości sinusa są trudne do obliczenia. Gimnazjaliści muszą umieć obliczyć sinus tylko dla kilku kątów. Inne możesz odczytać z tablic trygonometrycznych lub obliczyć za pomocą kalkulatora.
Im większy kąt ostry, tym większy jego sinus.
To jest ważne!
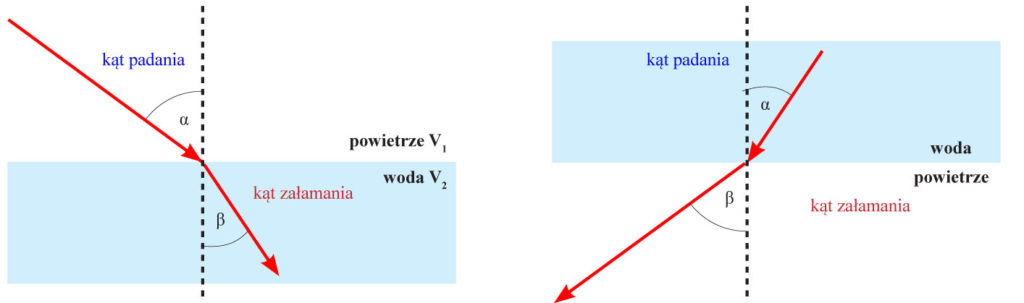
Załamanie światła następuje na granicy dwóch przezroczystych ośrodków. Poprowadź prostą prostopadłą do powierzchni rozgraniczającej te ośrodki. Kąt α (widoczny na rysunku), jaki tworzy promień padający z tą prostą prostopadłą, nazwijmy kątem padania. Kąt β zawarty między promieniem załamanym a prostą prostopadłą niech nazywa się kątem załamania.
Zapamiętaj prawo załamania!
Iloraz sinusa kąta padania i sinusa kąta załamania jest stały (nie zależy od kąta padania). Stałą wartość tego ilorazu nazywamy współczynnikiem załamania światła dla danych ośrodków. Możesz zapisać to symbolicznie:
Ponadto promień padający, załamany i prosta prostopadła do granicy ośrodków leżą w jednej płaszczyźnie.
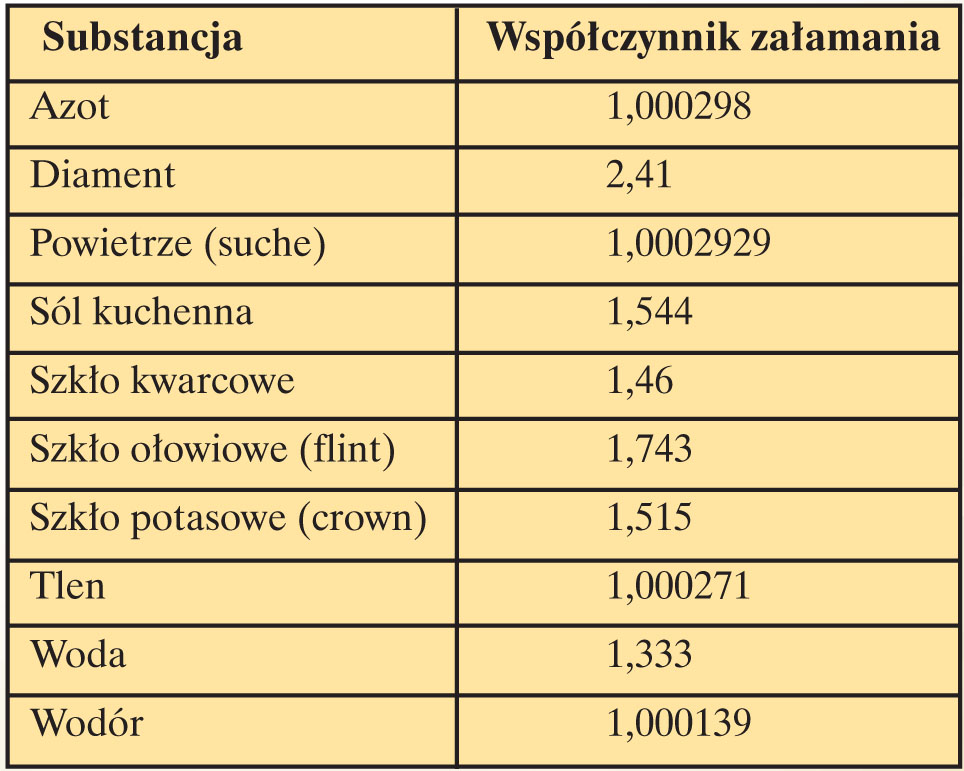
W tabeli masz podane współczynniki załamania kilku substancji w przypadku, gdy światło pada z próżni.
Od czego zależy wartość współczynnika załamania?
Okazuje się, że wartość współczynnika załamania zależy od szybkości światła w obydwu ośrodkach. A dokładniej:
v1 – szybkość światła w ośrodku, z którego światło pada
v2 – szybkość światła w ośrodku, do którego światło pada
Szybkość światła wynosi około 300 000 km/s. Skąd więc różne szybkości? Tę szybkość ma światło tylko w próżni. W innych ośrodkach światło porusza się wolniej.
Jakie wnioski wypływają z prawa załamania?
- Po pierwsze:
Gdy zwiększamy kąt padania, zwiększa się też kąt załamania.
- Po drugie:
Jeśli światło pada z ośrodka, w którym szybkość światła jest większa, do ośrodka o mniejszej szybkości światła, kąt załamania jest mniejszy niż kąt padania. Tak jest, gdy światło pada z powietrza do szkła.
Jeżeli natomiast szybkość światła jest mniejsza w pierwszym ośrodku niż w drugim, to kąt załamania jest większy niż kąt padania. Tak jest, gdy światło pada ze szkła do powietrza.
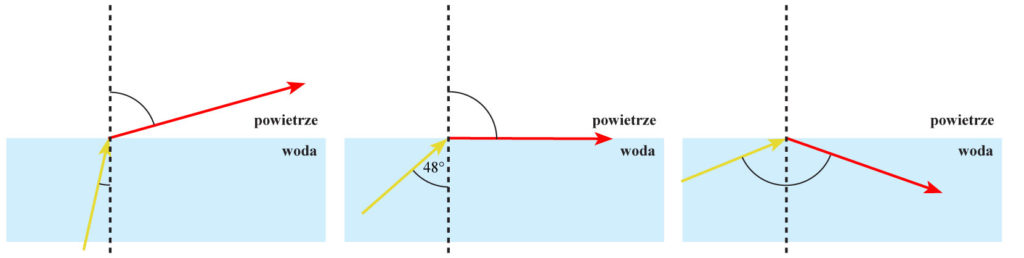
Co to jest całkowite wewnętrzne odbicie?
Wyobraź sobie, że światło pada z ośrodka o mniejszej prędkości światła do ośrodka, w którym prędkość światła jest większa, na przykład ze szkła do powietrza.
Zwiększenie α pociąga za sobą zwiększenie β. Ten wzrost ma jednak swoje granice. Co się stanie, gdy β osiągnie 90°? Dalsze zwiększanie tego kąta jest niemożliwe – promień wyszedłby z drugiego ośrodka i przestałby być promieniem załamanym! Wobec tego istnieje graniczny kąt padania, przy którym kąt załamania wynosi 90°.
Gdy kąt padania będzie większy niż kąt graniczny, do drugiego ośrodka nie wejdzie żadne światło. Co się z nim stanie? Odbije się całkowicie od granicy ośrodków zgodnie z prawem odbicia.
Zjawisko takie nosi nazwę całkowitego wewnętrznego odbicia. Właśnie to zjawisko jest wykorzystane w światłowodach. Dzięki niemu światło podróżuje wzdłuż światłowodu, nie wychodząc na zewnątrz. Bez strat można przesyłać nimi światło na duże odległości. Zjawisko całkowitego wewnętrznego odbicia ma duże znaczenie dla telekomunikacji. Na pewno widziałeś kiedyś w letni, upalny dzień „kałuże” na szosie? One też powstają dzięki temu zjawisku.
Teraz możesz rozwiązać zadanie!
Wiesz, że α = 45o, a n = 1,4. Musisz poszukać kąta załamania β. Skorzystasz oczywiście z prawa załamania:
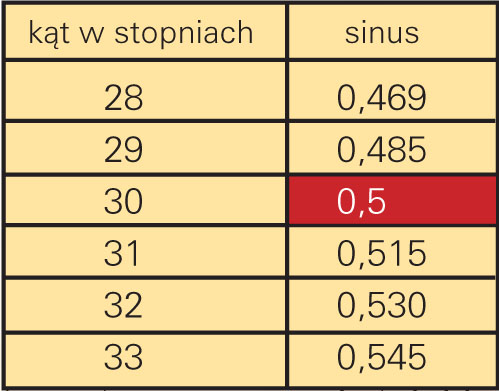
Sprawdź teraz w tabeli, jaki kąt odpowiada temu sinusowi.
Najbliższy tej wartości jest w naszej niezbyt dokładnej tabeli kąt 30º.
Odpowiedź: Kąt załamania wynosi około 30º.