Na koniec roku szkolnego nauczyciel wystawia każdemu klasyfikowanemu uczniowi ocenę z matematyki. Czy jakiś uczeń może ukończyć klasę bez oceny? Nie może. Czy jakiś uczeń może otrzymać na koniec roku szkolnego dwie lub trzy oceny z matematyki? Nie może. Każdemu uczniowi przyporządkowano dokładnie jedną końcową ocenę z matematyki. I na tym właśnie polega funkcja…
Funkcja – co to takiego?
Funkcją ze zbioru A do zbioru B nazywamy takie przyporządkowanie, że każdemu elementowi zbioru A przyporządkowany jest dokładnie jeden element zbioru B.
- Elementy zbioru A są argumentami tej funkcji, a elementy zbioru B – wartościami funkcji.
- Zbiór A to dziedzina tej funkcji, zbiór B – przeciwdziedzina.
Zwróć uwagę, że…
Z powyższej definicji funkcji wynika kilka ważnych faktów:
- Każdemu argumentowi musi być przyporządkowana wartość (inaczej przyporządkowanie nie jest funkcją).
- Każdemu argumentowi jest przyporządkowana tylko jedna wartość.
- Jedna wartość może być przyporządkowana kilku argumentom (np. kilka osób otrzymało tę samą ocenę).
Które przyporządkowanie jest funkcją?
Oto przykłady kilku różnych przyporządkowań. Spróbuj ustalić, które z tych przyporządkowań są funkcjami, a które nie. Dla funkcji ustal dziedzinę i przeciwdziedzinę.
1. Każdemu uczniowi w Twojej szkole przyporządkowano numer w dzienniku (w bieżącym roku szkolnym).
2. Każdej klasie w Twojej szkole przyporządkowano liczbę uczniów.
3. Każdej klasie w Twojej szkole przyporządkowano uczniów tej klasy.
4. Każdemu samochodowi zarejestrowanemu w Polsce przyporządkowano numer rejestracyjny.
5. Każdej liczbie naturalnej mniejszej od 20 przyporządkowano jej naturalne dzielniki (różne od niej samej).
Rozwiązania:
1. To przyporządkowanie jest funkcją. Każdy uczeń ma dokładnie jeden numer. Zauważ, że jeden i ten sam numer może mieć wiele osób (w różnych klasach), ale to nie przeszkadza, by przyporządkowanie mogło być funkcją. Dziedziną tej funkcji jest zbiór uczniów Twojej szkoły, a przeciwdziedziną – zbiór liczb naturalnych od jeden do liczby uczniów w najliczniejszej klasie.
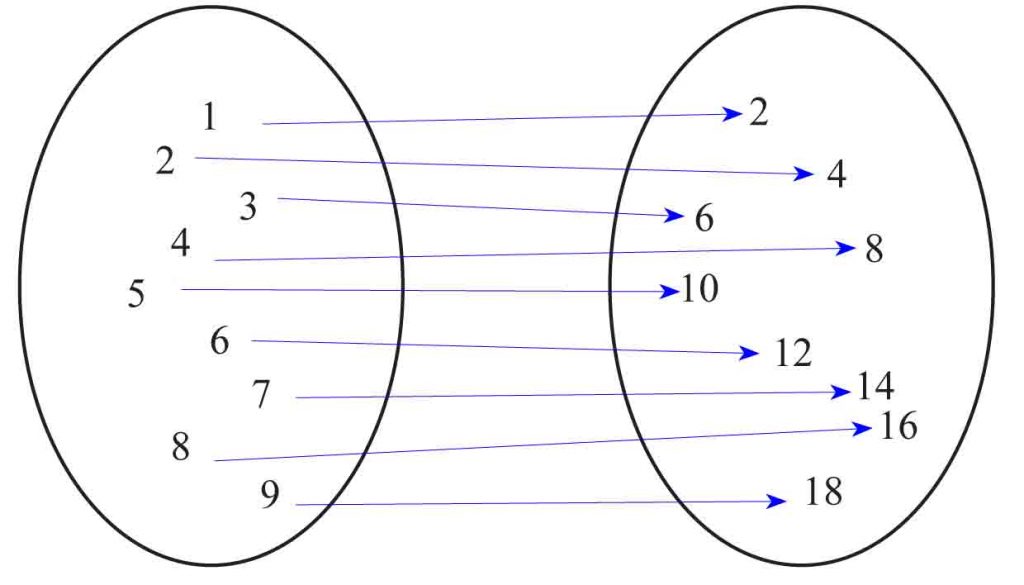
2. To oczywiście też jest funkcja. Dziedziną jest zbiór klas, a przeciwdziedziną zbiór liczb uczniów. Na grafie funkcja ta może wyglądać na przykład tak:
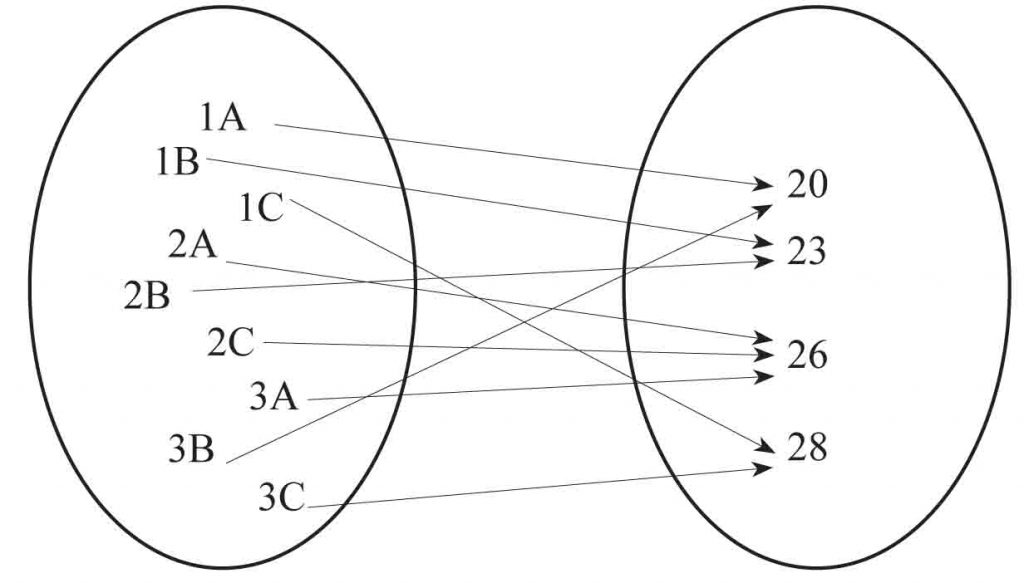
3. To przyporządkowanie nie jest funkcją. Dlaczego? Dlatego, że argumentom (klasom) przyporządkowano wiele wartości (każdej klasie przyporządkowano wszystkich jej uczniów).
4. To przyporządkowanie jest funkcją. Każdy samochód aktualnie zarejestrowany ma dokładnie jeden numer rejestracyjny. Zbiór samochodów zarejestrowanych w Polsce to dziedzina, a zbiór numerów rejestracyjnych to przeciwdziedzina. Ta funkcja ma dodatkową specyficzną własność. Zauważ, że każdy samochód ma inny numer rejestracyjny, a więc każda wartość funkcji jest przyjmowana tylko raz. O takiej funkcji mówimy, że jest różnowartościowa.
5. To przyporządkowanie funkcją nie jest, bo niektórym liczbom przyporządkować trzeba więcej niż jedną wartość.
Jedna funkcja – kilka sposobów jej zapisania
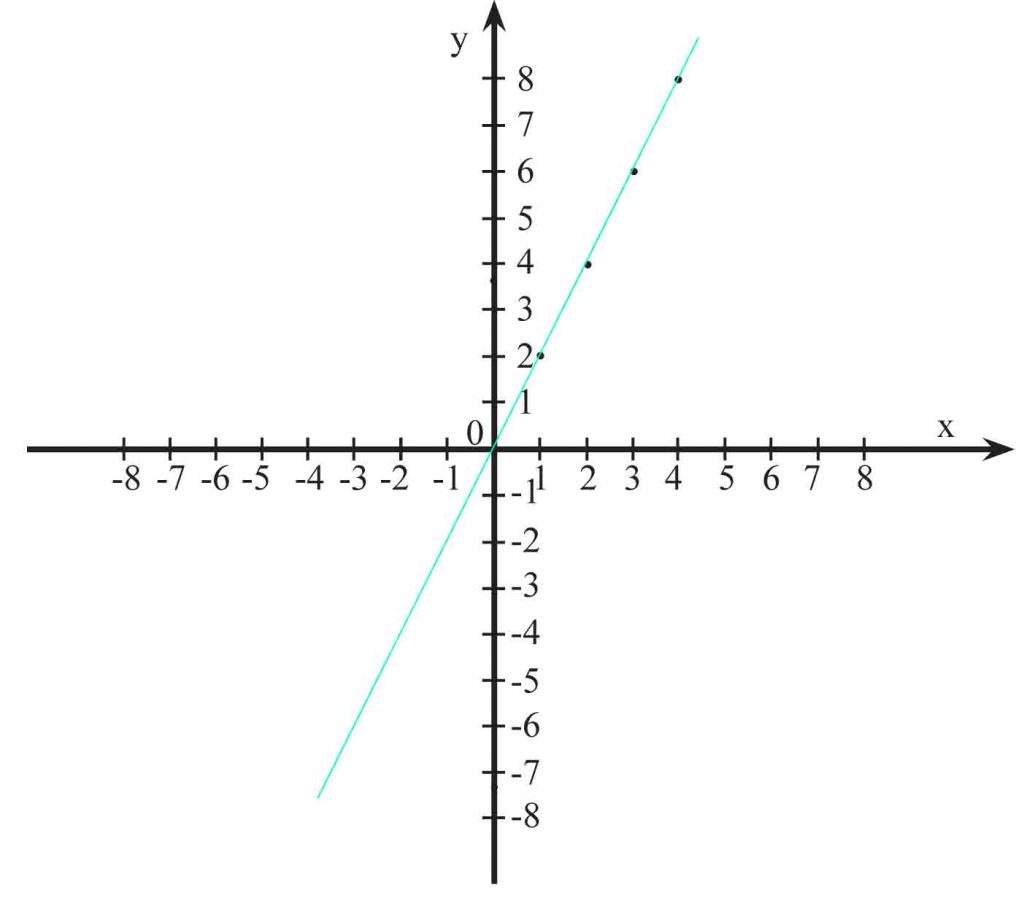
Funkcję można zapisać na wiele różnych sposobów – na przykład: grafem, wykresem, wzorem, opisem słownym. Weźmy funkcję, która każdej liczbie rzeczywistej przyporządkowuje dwukrotność tej liczby. Funkcję tę przedstawimy następująco:
Za pomocą grafu:
Za pomocą wykresu:
Za pomocą wzoru:
y=2x
To jest ważne!
Pamiętaj, że dziedziną i przeciwdziedziną mogą być dowolne zbiory. W szkole najczęściej zajmujemy się funkcjami liczbowymi, to znaczy takimi, że dziedzina i przeciwdziedzina są zbiorami liczbowymi.
Na egzaminie spodziewaj siê takiego zadania:
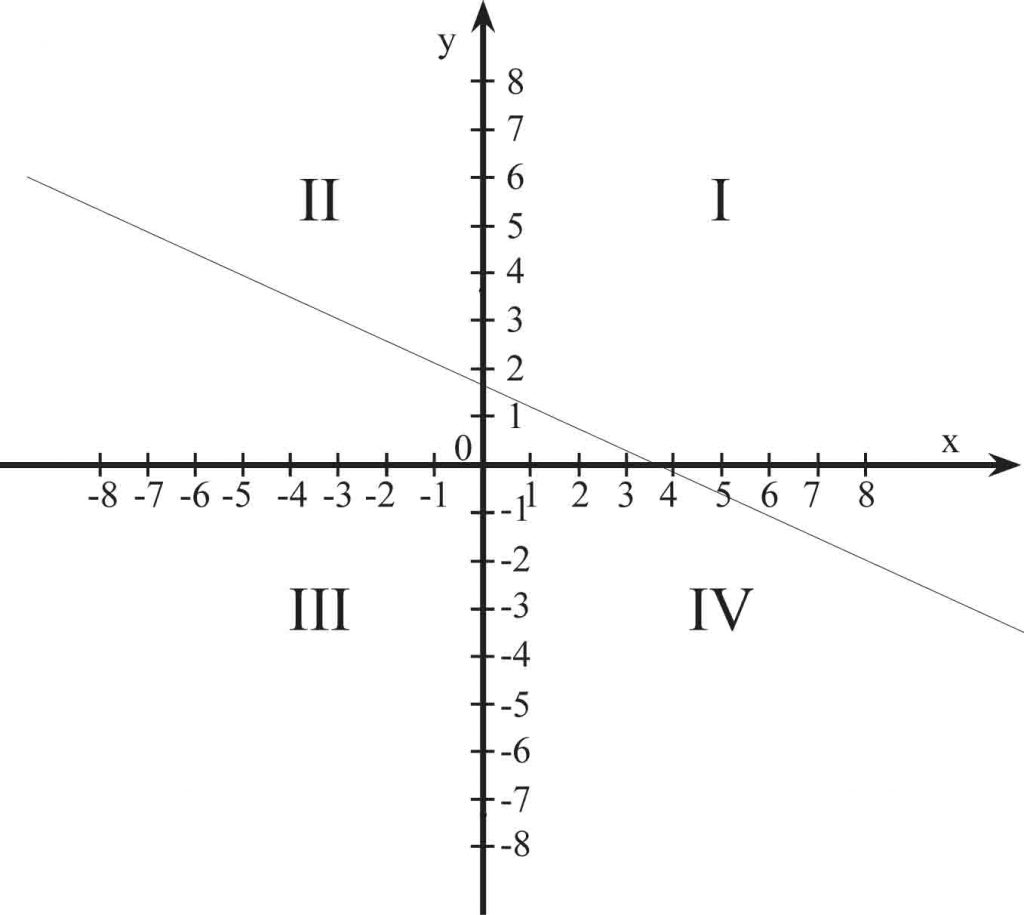
Wykres pewnej funkcji liniowej przechodzi przez I, II i IV ćwiartkę układu współrzędnych. Zatem funkcja ta jest:
A. rosnąca,
B. malejąca,
C. stała,
D. tego nie da się określić.
Jak to rozwiązać?
Przede wszystkim musisz wiedzieć, jak przebiegają numery ćwiartek w układzie współrzędnych. Musisz też wiedzieć, że wykresem funkcji liniowej jest linia prosta.
Ćwiartki ponumeruj tak:
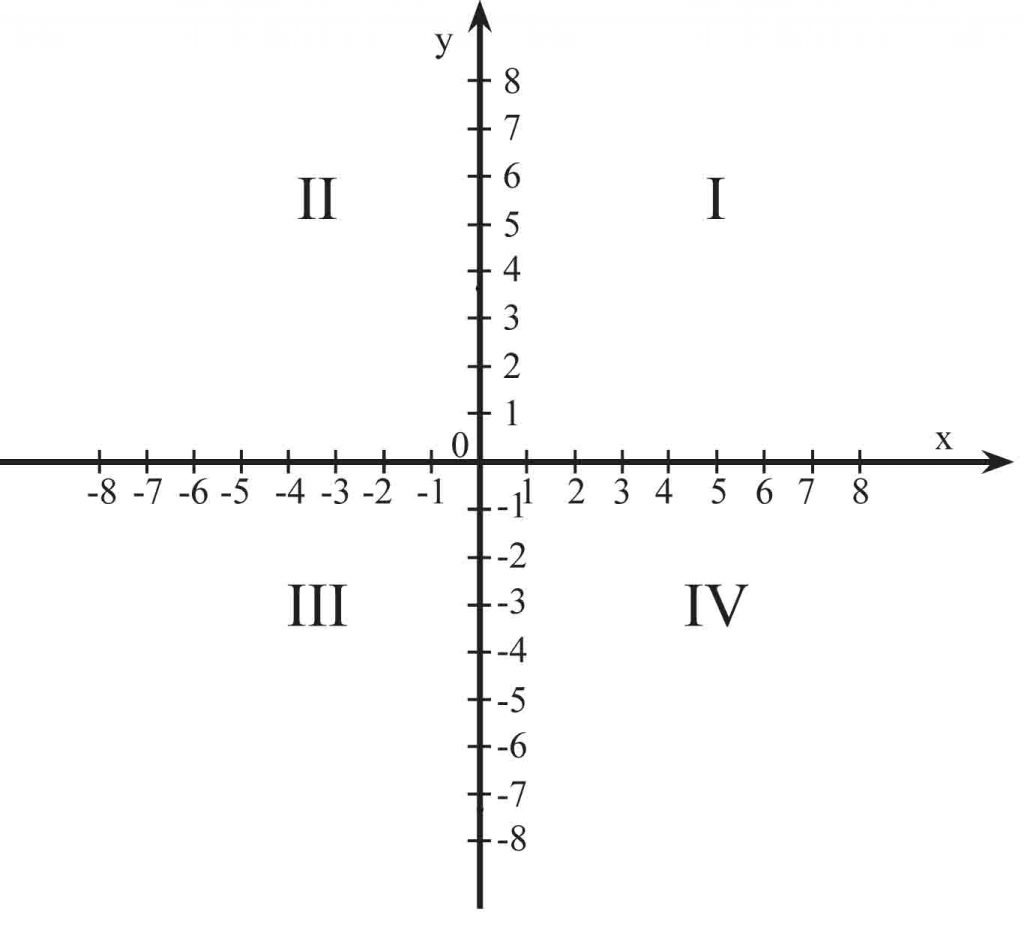
Jeśli zatem linia prosta przechodzi przez I, II i IV ćwiartkę, to masz do czynienia z funkcją malejącą (wraz ze wzrostem argumentów maleją wartości funkcji).
Co koniecznie musisz powtórzyć przed egzaminem?
- Odczytywanie współrzędnych punktów w układzie współrzędnych.
- Rysowanie wykresu funkcji liniowej na podstawie wzoru.
- Pisanie wzorów funkcji liniowej, gdy masz podane dwa punkty, przez które przechodzi jej wykres.
- Posługiwanie się twierdzeniem Pitagorasa – obliczanie odległości punktów w układzie współrzędnych.
Zadanie
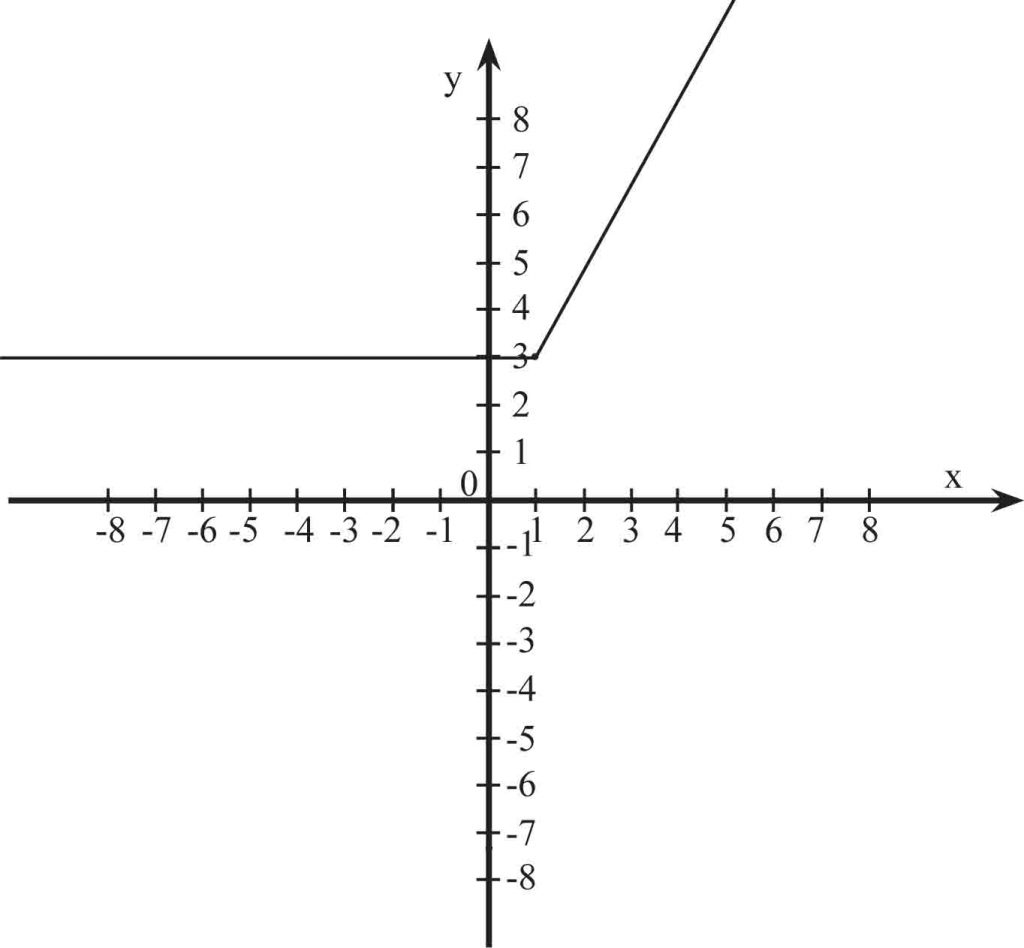
Narysuj wykres funkcji:
Zobacz, dla jakich liczb istnieją przyporządkowane wartości.
Dla liczb mniejszych niż jeden przyporządkowana jest wartość 3, a dla liczb większych bądź równych jeden wartość jest przyporządkowana według wzoru y=2x+1
Co jest dziedziną, a co przeciwdziedziną funkcji?
Dziedziną jest zbiór wszystkich liczb rzeczywistych (R), a przeciwdziedziną – przedział 〈3; +∞)
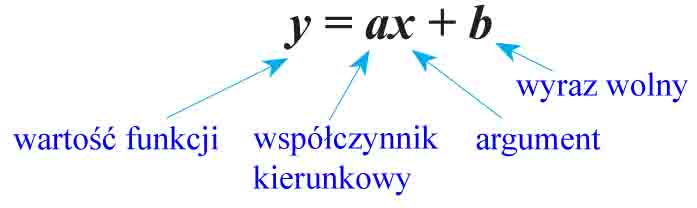
Funkcja liniowa:
Współczynnik kierunkowy decyduje o monotoniczności funkcji liniowej, to znaczy:
- Jeśli współczynnik kierunkowy jest ujemny, to funkcja jest malejąca.
- Jeśli współczynnik kierunkowy jest dodatni, to funkcja jest rosnąca.
- Jeśli współczynnik kierunkowy jest równy zero, to funkcja jest stała.
Wyraz wolny determinuje miejsce przecięcia się wykresu funkcji liniowej z osią rzędnych (to znaczy z osią Y). Punkt ten ma współrzędne (),b).
Miejsce zerowe funkcji to taki argument, któremu przyporządkowana jest wartość zero.
Jeśli funkcja liniowa nie jest stała, to ma dokładnie jedno miejsce zerowe i jest ono równe: ![]() .
.