Pojęcie funkcji
Pojęcie funkcji w matematyce jest pojęciem podstawowym. Na nim opiera się wiele innych pojęć matematycznych. Należałoby zatem przypomnieć sobie, co oznacza słowo „funkcja”, oraz wszystko to, co wiąże się z tym słowem, w zakresie wiadomości poznanych w szkole podstawowej.
Rozważmy więc kilka przykładów wprowadzających ten temat.
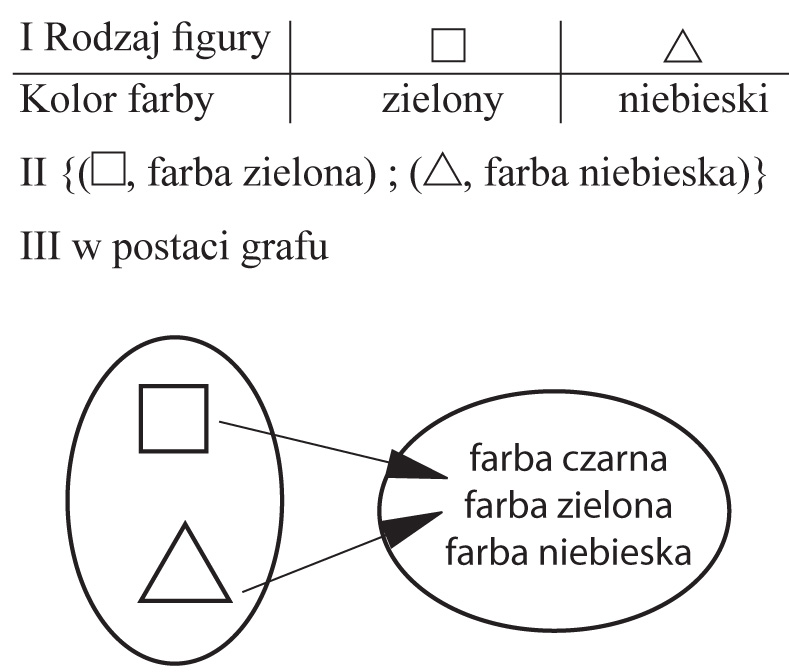
1) Mamy
Chcemy te figury pomalować używając do każdej z nich tylko jednej farby. Przypuśćmy, że obie figury pomalowaliśmy na zielono. Do zanotowania tego możemy użyć jednego z trzech następujących symbolicznych zapisów:
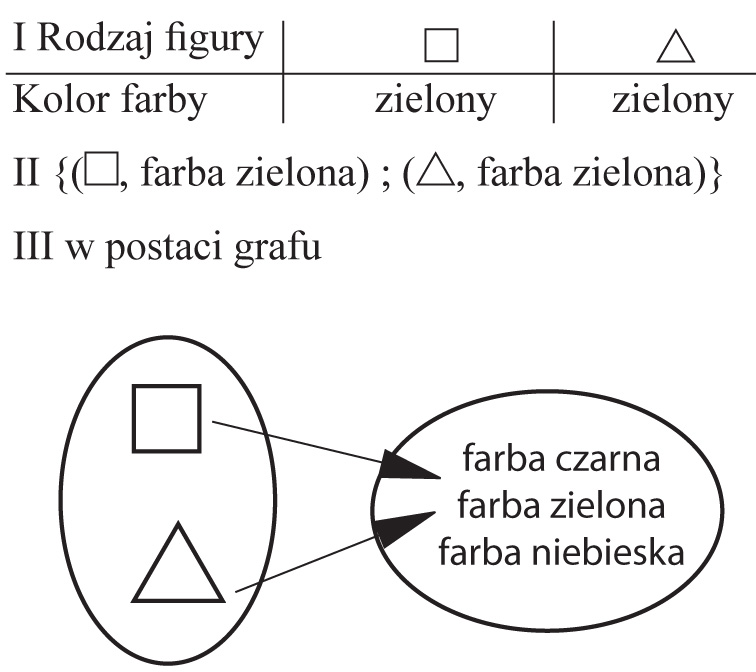
2) Pomalujmy teraz figury zbioru ![]() tak, aby kwadrat był zielony, zaś trójkąt niebieski.
tak, aby kwadrat był zielony, zaś trójkąt niebieski.
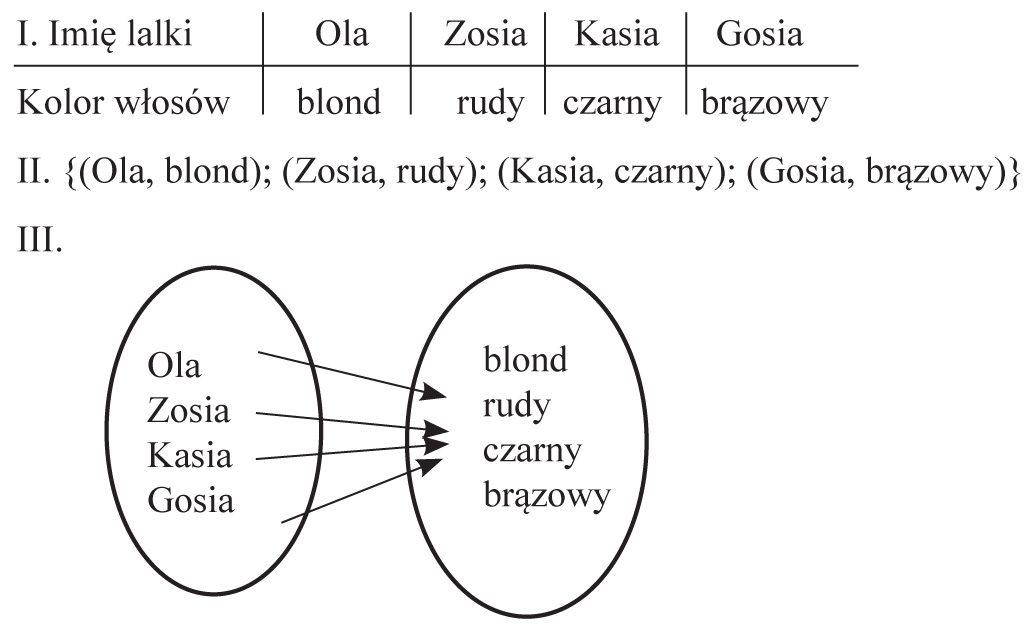
3) Niech naszym pierwszym zbiorem będzie zbiór lalek o imionach {Ola, Zosia, Kasia, Gosia}, a zbiorem drugim – zbiór kolorów ich włosów {blond, rudy, czarny, brązowy}. Przyporządkujmy każdej lalce kolor jej włosów i zapiszmy to:
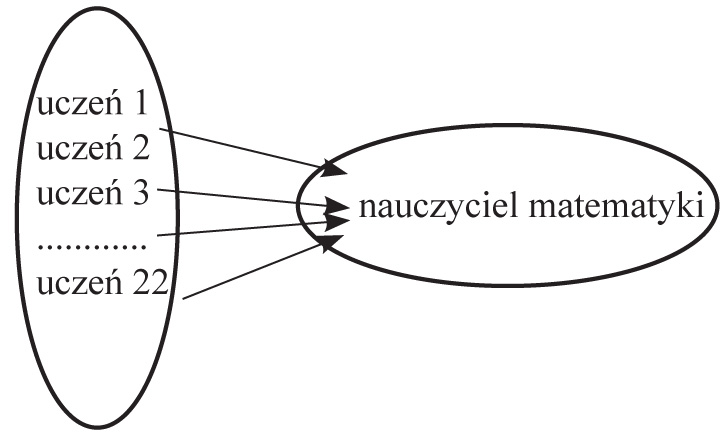
4) Zbiór pierwszy A, to zbiór uczniów klasy VIIIa, a zbiór drugi B, to zbiór nauczycieli matematyki uczących klasę VIIIa. Ten drugi zbiór jest jednoelementowy. Przyporządkujmy każdemu uczniowi klasy VIIIa jego nauczyciela matematyki.
Przedstawmy to na GRAFIE:
Każdy uczeń klasy VIIIa ma przyporządkowanego jednoznacznie nauczyciela matematyki uczącego go.
Jeżeli dane są dwa zbiory A i B, i jeśli każdemu elementowi zbioru A został przyporządkowany dokładnie jeden element zbioru B, to przyporządkowanie takie nazywamy funkcją określoną na zbiorze A o wartościach w zbiorze B.
Zbiór A nazywamy dziedziną funkcji lub zbiorem argumentów funkcji.
Zbiór B nazywamy zbiorem wartości funkcji lub przeciwdziedziną.
We wszystkich powyższych przykładach mieliśmy do czynienia z funkcjami.
Praktycznie rzecz biorąc, aby PRZYPORZĄDKOWANIE można było nazwać FUNKCJĄ, spełnione muszą być DWA WARUNKI.
- I. Każdy element zbioru A (dziedziny) musi mieć przyporządkowanie.
- II. Każdemu elementowi zbioru A przyporządkować można jeden i tylko jeden element zbioru B.
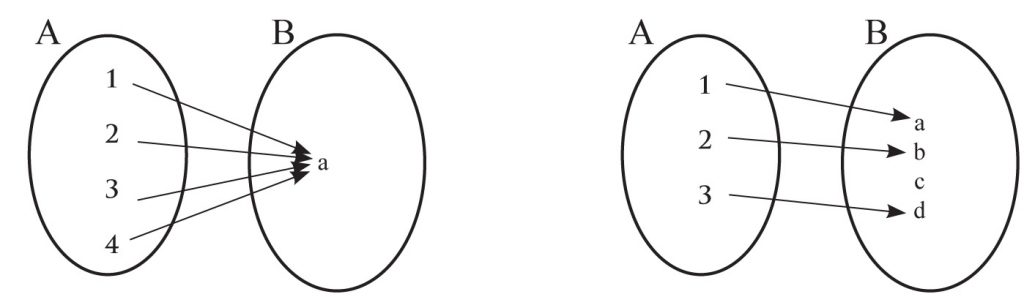
Zastanówmy się czy podane poniżej przyporządkowania są funkcjami:
1) 2)
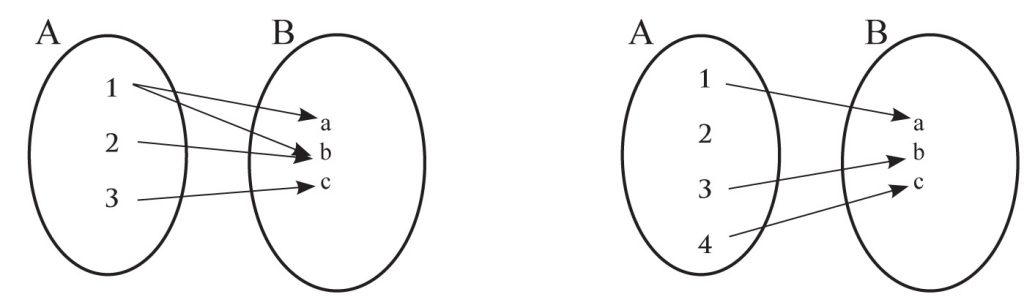
nie, bo 1 ma przyporządkowane nie, bo 2 nie ma
dwa elementy a i b przyporządkowania
tak, bo spełnione są te dwa warunki tak, bo spełnione są te
Jest to funkcja stała (gdyż każdy element dwa warunki
zbioru A ma przyporządkowany ten sam
element zbioru B)
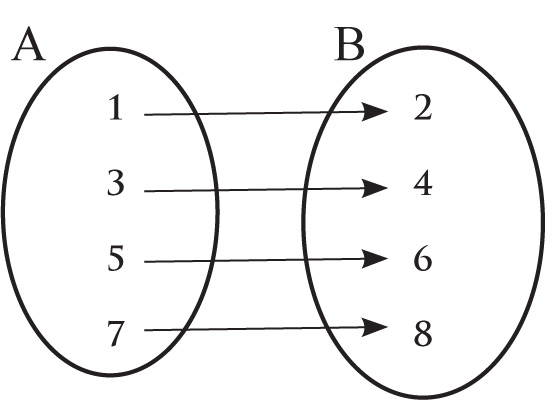
Może się tak zdarzyć że, oba zbiory A i B są liczbowe. Wtedy funkcja też nosi nazwę liczbowej, np.:
dla argumentu 1 wartość funkcji wynosi 2
dla argumentu 3 wartość funkcji wynosi 4
dla argumentu 5 wartość funkcji wynosi 6
dla argumentu 7 wartość funkcji wynosi 8
można powiedzieć też inaczej, że:
2 jest wartością funkcji w punkcie 1
4 jest wartością funkcji w punkcie 3
6 jest wartością funkcji w punkcie 5
8 jest wartością funkcji w punkcie 7
co zapisujemy
f(1) = 2
f(3) = 4
f(5) = 6
f(7) = 8
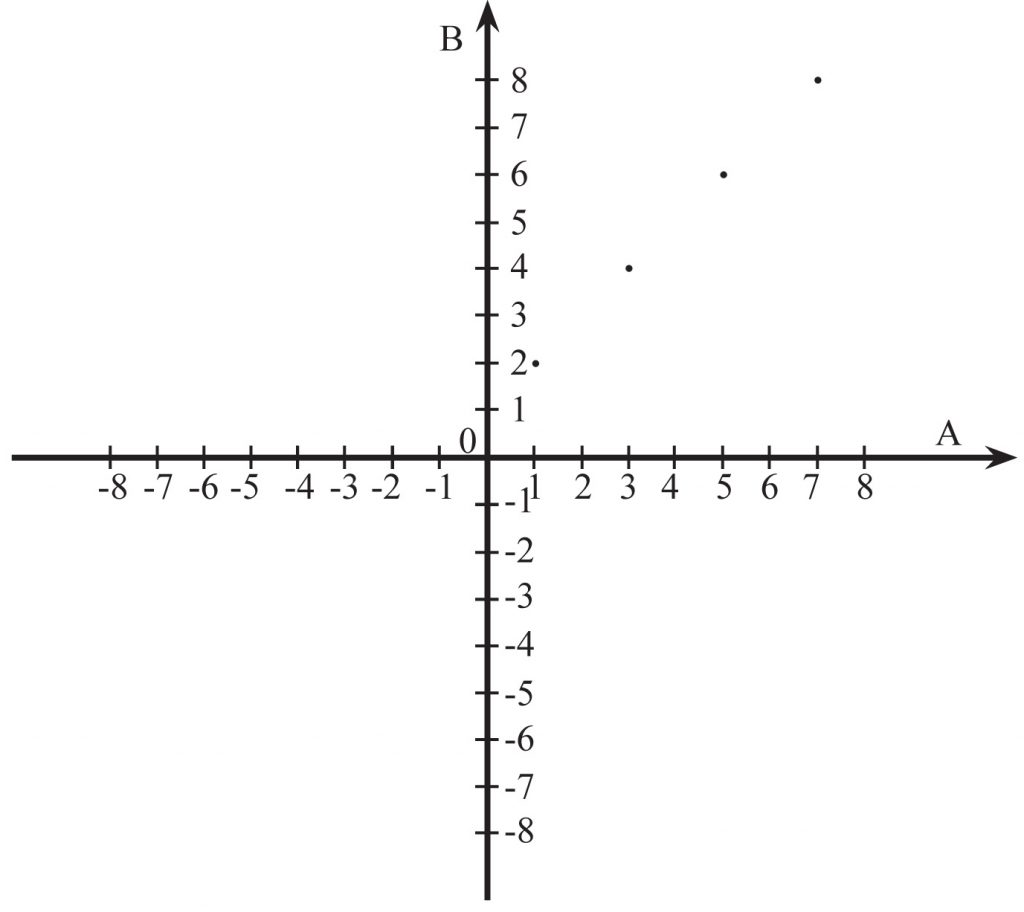
Powyższą funkcję można opisać także przy pomocy WYKRESU w prostokątnym układzie współrzędnych na płaszczyźnie:
lub przy pomocy WZORU:
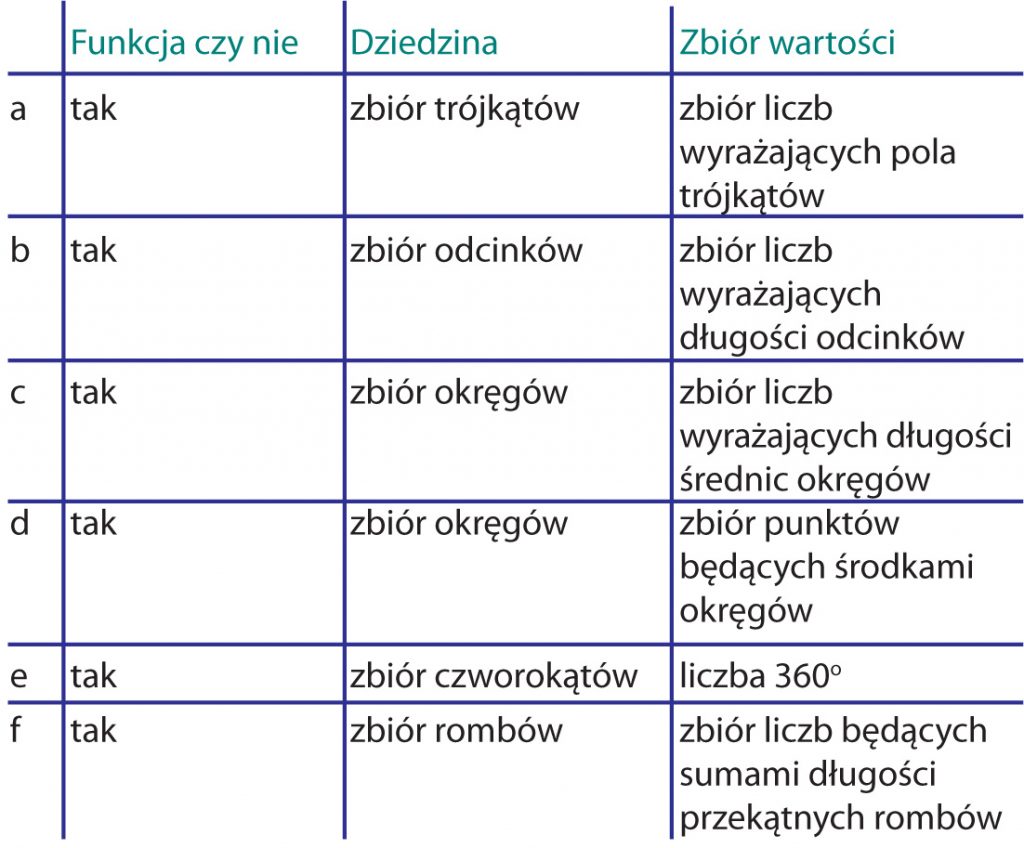
Zadanie 1
Zbadaj, czy następujące przyporządkowanie określa pewną funkcję. Jeśli tak, to znajdź jej dziedzinę i zbiór wartości:
a) każdemu trójkątowi przyporządkowujemy jego pole,
b) każdemu odcinkowi przyporządkowujemy jego długość,
c) każdemu okręgowi przyporządkowujemy długość jego średnicy,
d) każdemu okręgowi przyporządkowujemy jego środek,
e) każdemu czworokątowi wypukłemu przyporządkowujemy sumę miar jego kątów wewnętrznych,
f) każdemu rombowi przyporządkowujemy sumę długości jego przekątnych
Odpowiedź:
Zadanie 2
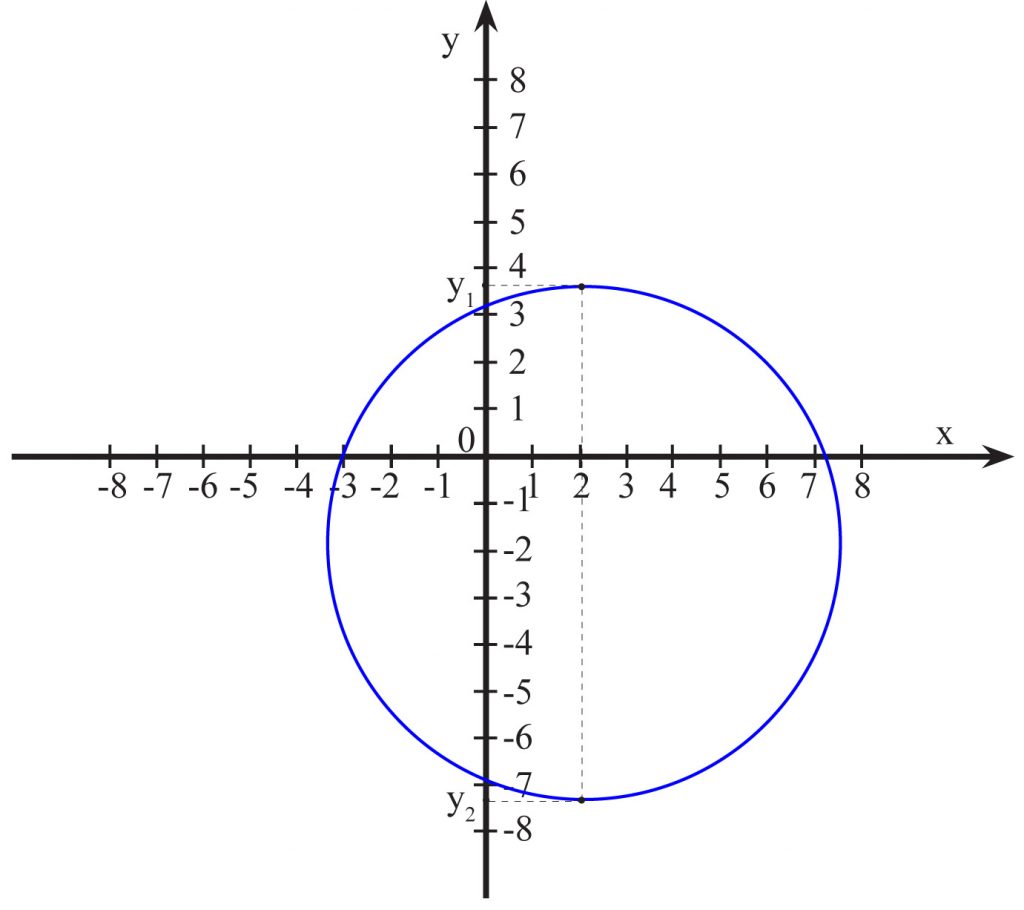
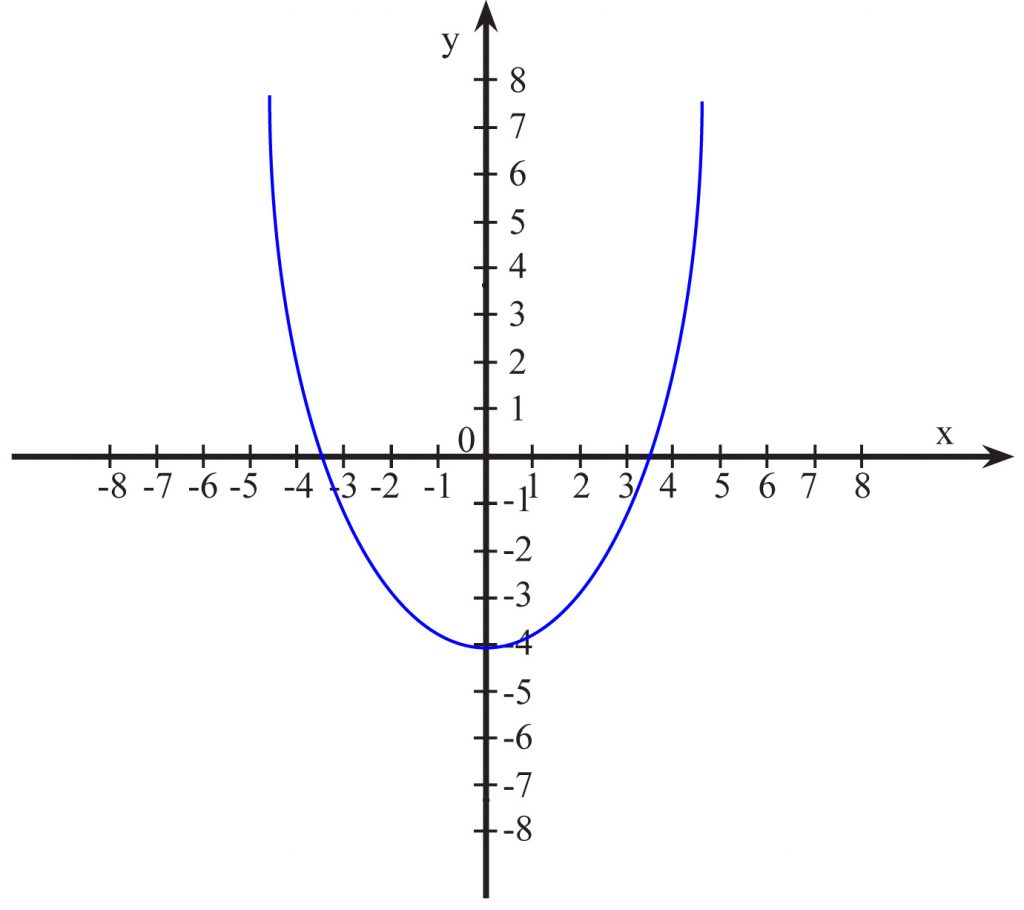
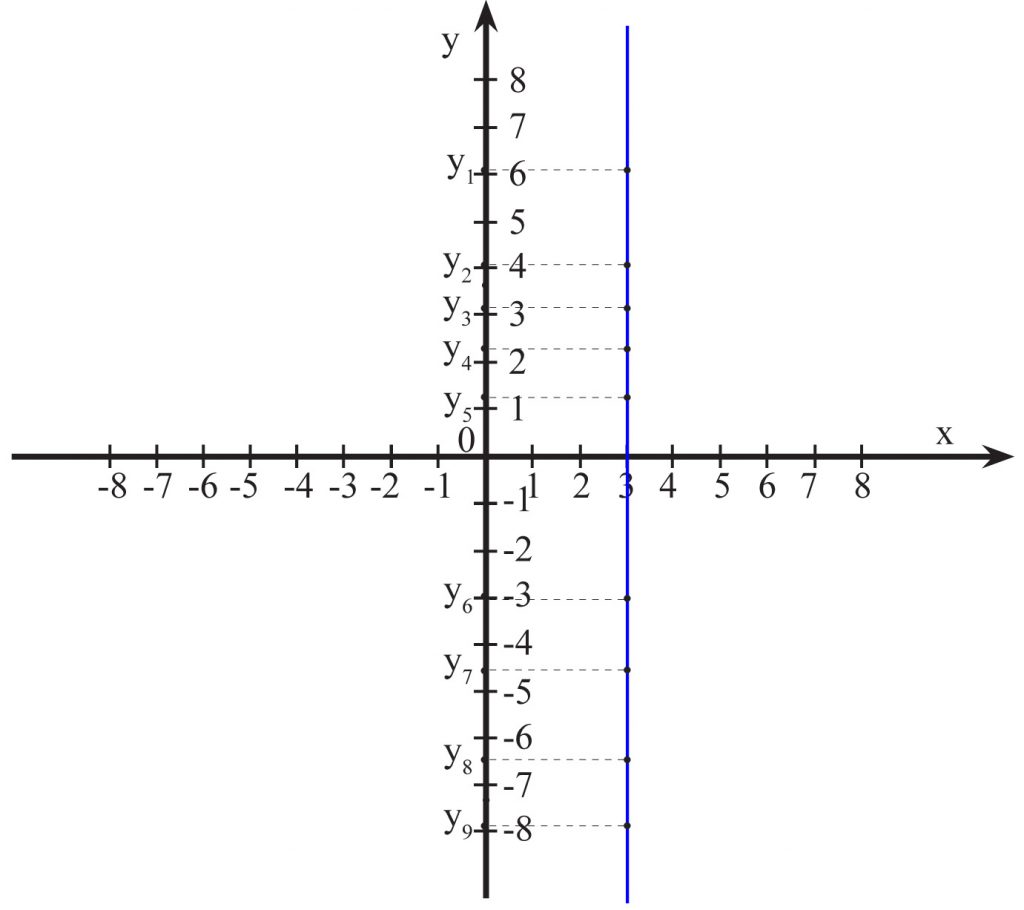
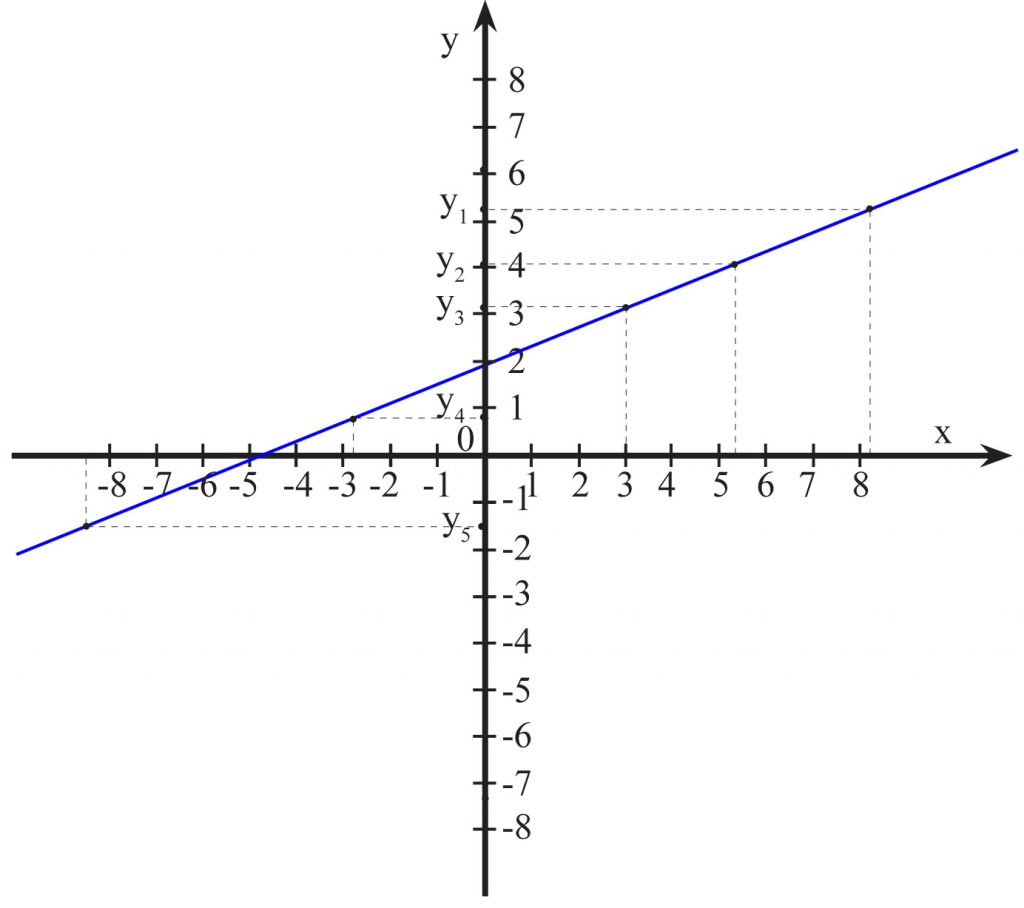
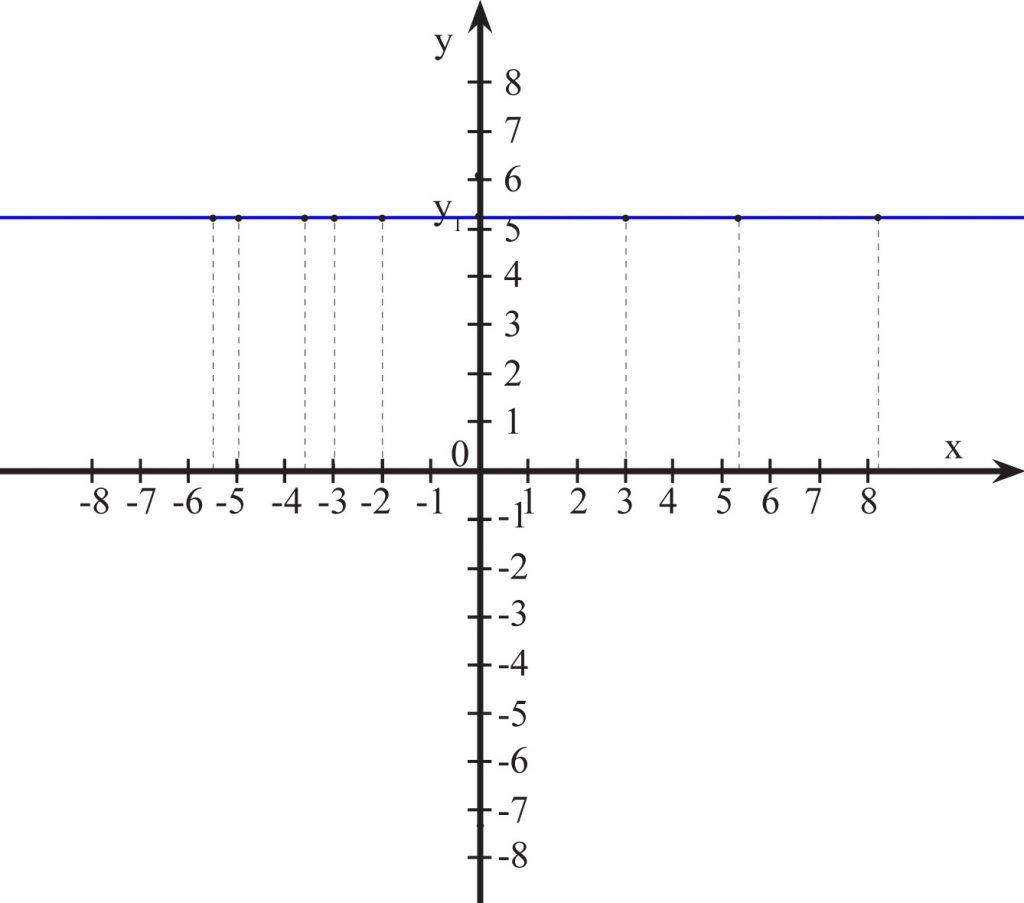
Czy poniższe wykresy przedstawiają przyporządkowania zwane funkcjami?
nie, bo np. x=1
odpowiadają y1 i y2
tak, bo każdemu x odpowiada dokładnie jedna wartość y
nie, bo x=2 odpowiada nieskończenie wiele wartości y
tak, bo każdemu x odpowiada dokładnie jedna wartość y
tak, bo każdemu x odpowiada dokładnie jedna wartość y
nie, bo np. x=3 odpowiadają dwie wartości y1 i y2
Zadanie 3
Czy poniższe przyporządkowania są funkcjami?
a) każdej matce przyporządkowano jej dzieci.
b) każdemu dziecku przyporządkowano jego matkę.
c) każdemu uczniowi przyporządkowano jego ocenę z matematyki na koniec semestru.
d) każdemu pojazdowi przyporządkowano jego numer rejestracyjny.
e) każdej kobiecie przyporządkowano ilość jej okryć zimowych.
f) każdej szkole przyporządkowano ilość uczniów uczęszczających do niej.
Odpowiedzi:
a) nie – gdyż są matki mające więcej niż jedno dziecko.
b) tak – gdyż każde dziecko ma lub miało jedną matkę (biologiczną).
c) tak – gdyż każdy uczeñ ma jedną ocenę z matematyki na koniec semestru.
d) tak – gdyż każdy pojazd ma jeden numer rejestracyjny.
e) nie – gdyż są kobiety mające więcej niż jedno okrycie zimowe lub nie mające wcale takich okryć.
f) nie – gdyż ilość uczniów jest większa niż jeden.
Zadanie 4
Czy przyporządkowania podane w tabelce są funkcją
a)
x -1 1 0 1 2
y 1 0 1 -1 2
nie, gdyż 1 przyporządkowano dwie wartości 0 i -1
b)
x 2 3 4 2
y 1 0 -2 -3
nie, gdyż 2 przyporządkowano dwie wartości 1 i -3
c)
x -3 0 3 4
y 0 4 0 5
tak, gdyż każdy x ma przyporządkowany tylko jeden element y
d)
x -1 -1 -1 -1
y -3 0 1 2
nie, gdyż -1 przyporządkowano aż cztery wartości -3, 0, 1 i 2
Wiemy już, jakie przyporządkowanie nazywamy funkcją.
A jak można opisać (wyrazić) jakąkolwiek funkcję?
W poprzednich przykładach funkcje opisywane były przy pomocy:
1) grafu
2) tabelki
3) wykresu
4) par uporządkowanych (w których pierwszy element oznacza argument, a drugi – wartość funkcji)
5) opisu słownego (jak np. w zadaniu 3)
6) wzoru
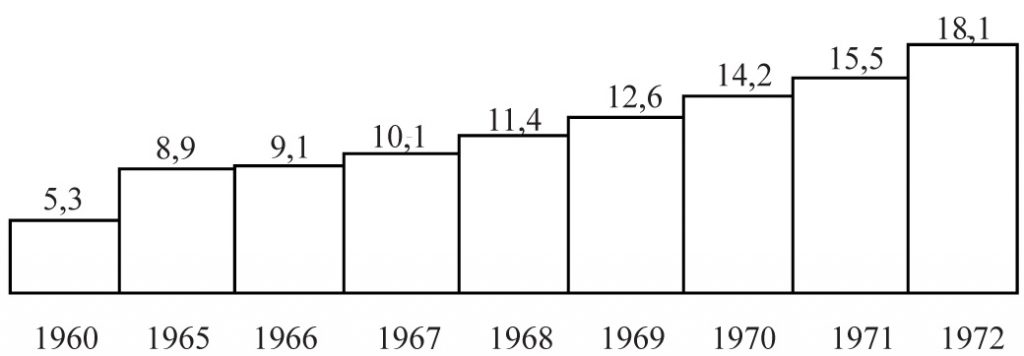
Można też opisać funkcję przy pomocy diagramu np.:
Dziedziną funkcji jest tu zbiór lat 1960 – 1972, a zbiorem wartości jest wielkość polskiego eksportu w poszczególnych latach.
A teraz zabawmy się w przedstawienie różnych opisów tej samej funkcji, którą określamy następująco:
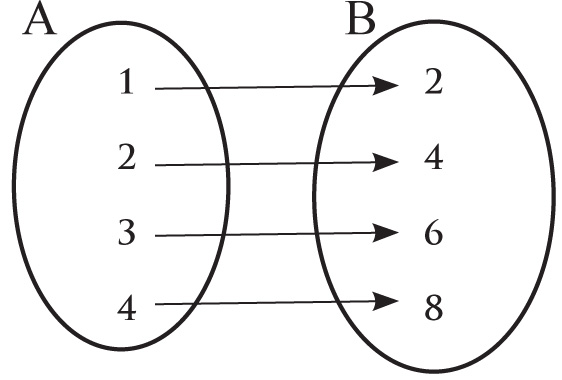
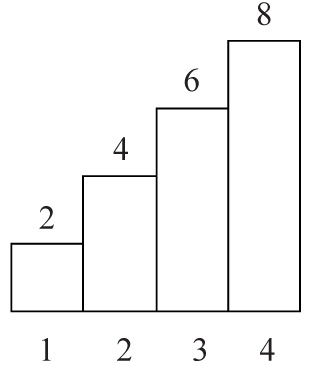
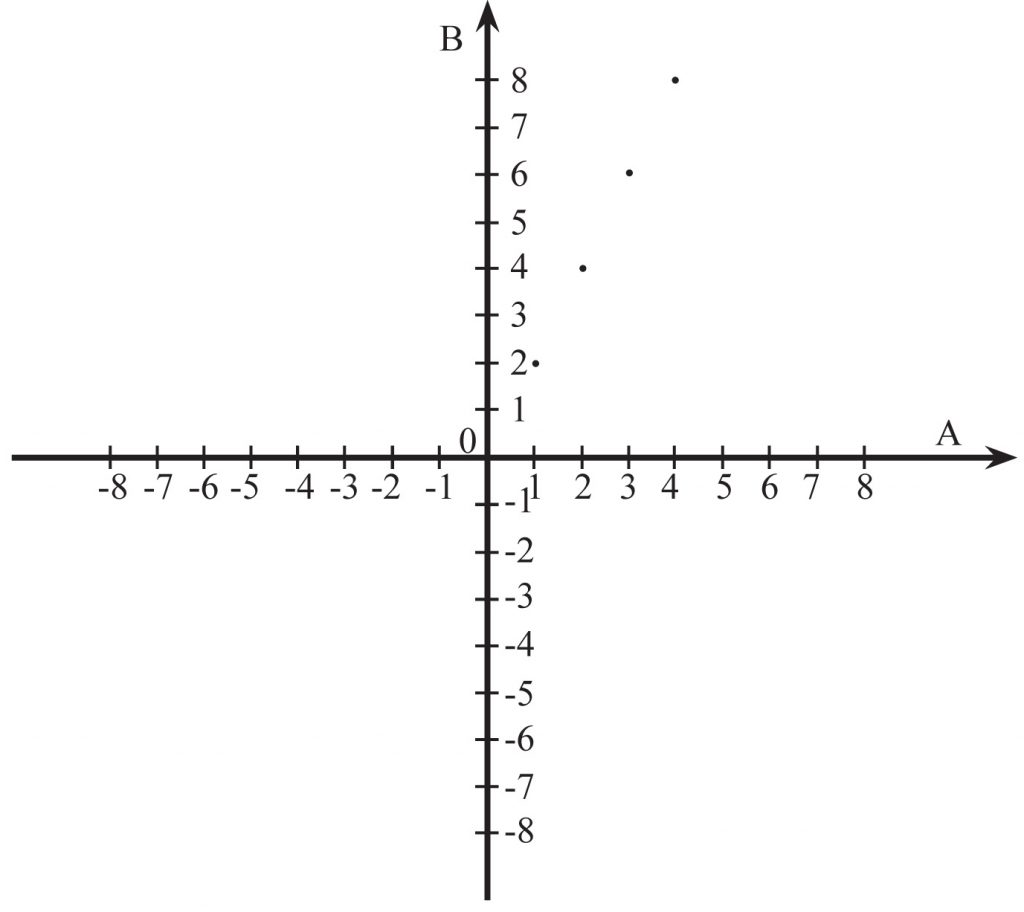
Funkcja f odwzorowuje zbiór X={1, 2, 3, 4} w zbiór Y={2, 4, 6, 8} według wzoru y = 2x.
Dziedziną funkcji jest zbiór X, zbiorem wartości funkcji jest zbiór Y.
A oto sposoby opisu tej funkcji:
a) wzór: y = 2x dla x
b) graf:
gdyż dla
- x=1→y=2·1=2 (możemy zapisać też f(1) = 2)
- x=2→y=2·2=4 (możemy zapisać też f(2) = 4)
- x=3→y=2·3=6 (możemy zapisać też f(3) = 6)
- x=4→y=2·4=8 (możemy zapisać też f(4) = 8)
c) tabelka:
d) zbiór par uporządkowanych:
{(1, 2); (2, 4); (3, 6); (4, 8)}
e) opis słowny:
Każdej liczbie ze zbioru X = {1, 2, 3, 4} przyporządkowano liczbę dwa razy większą.
f) diagram:
g) wykres:
Możemy zadać sobie teraz pytanie – Jak dziedzina funkcji wpływa na wykres tej funkcji?
Rozważmy następujący przykład:
Wykonaj wykresy funkcji:
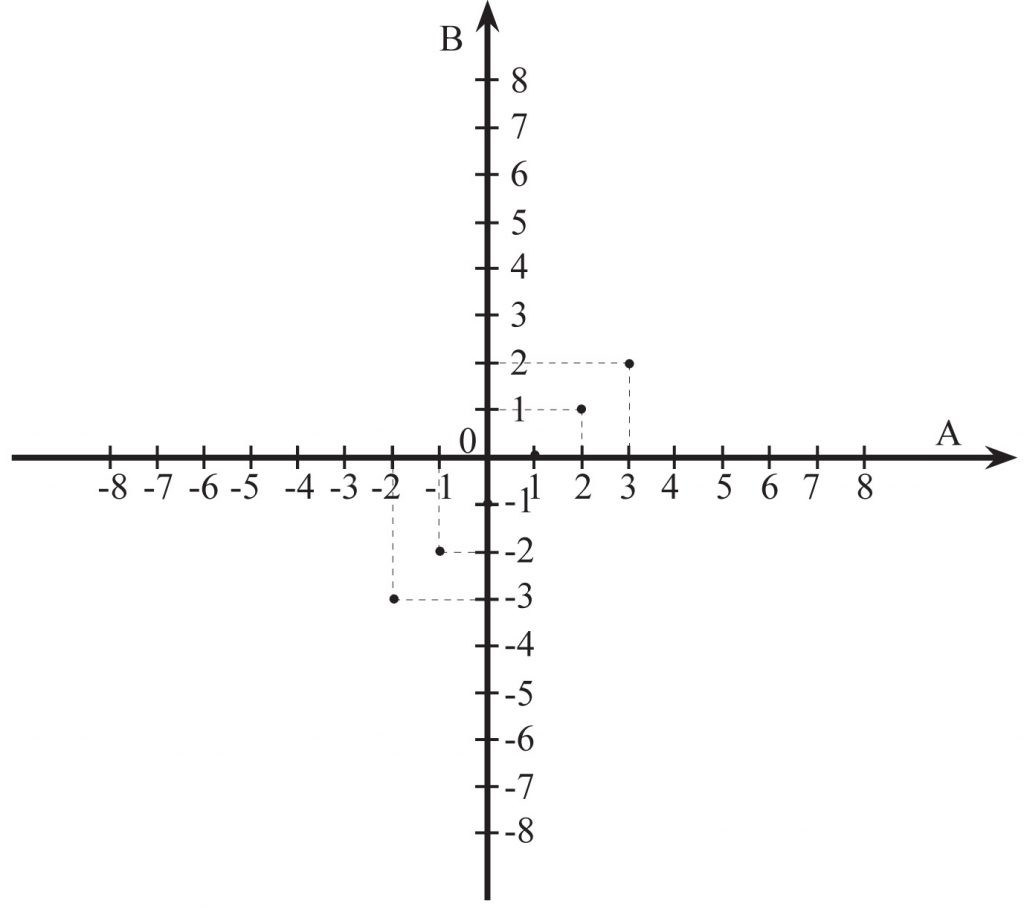
a) y = x – 1 dla x{-2, -1, 0, 1, 2, 3}
f(-2) = -2 – 1 = -3
f(-1) = -1 – 1 = -2
f(0) = 0 – 1 = -1
f(1) = 1 – 1 = 0
f(2) = 2 – 1 = 1
f(3) = 3 – 1 = 2
Wykresem jest zbiór sześciu punktów
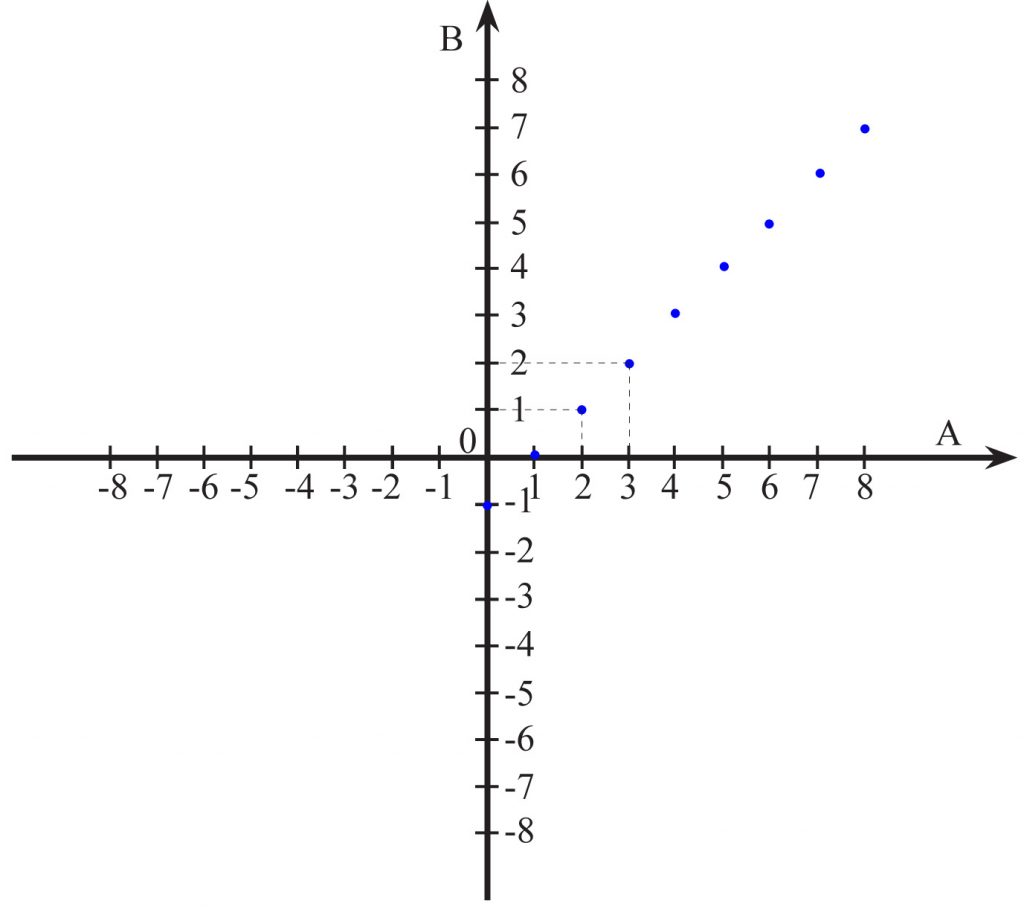
b) y = x – 1 dla x∈N (zbioru liczb naturalnych czyli x{0, 1, 2, 3, …})
Wykresem jest zbiór nieskończenie wielu punktów.
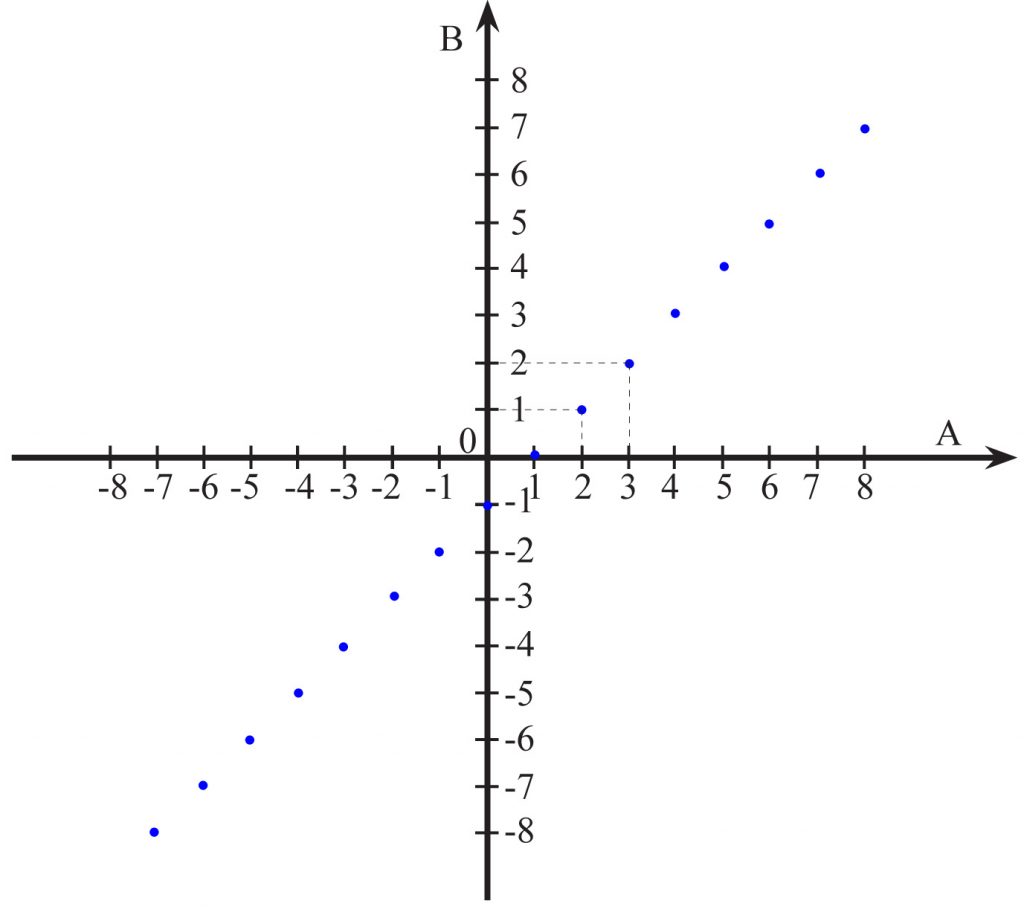
c) y = x – 1 dla xC (zbioru liczb całkowitych, czyli
x{… -2, -1, 0, 1, 2, 3, …})
Wykresem jest zbiór nieskończenie wielu punktów.
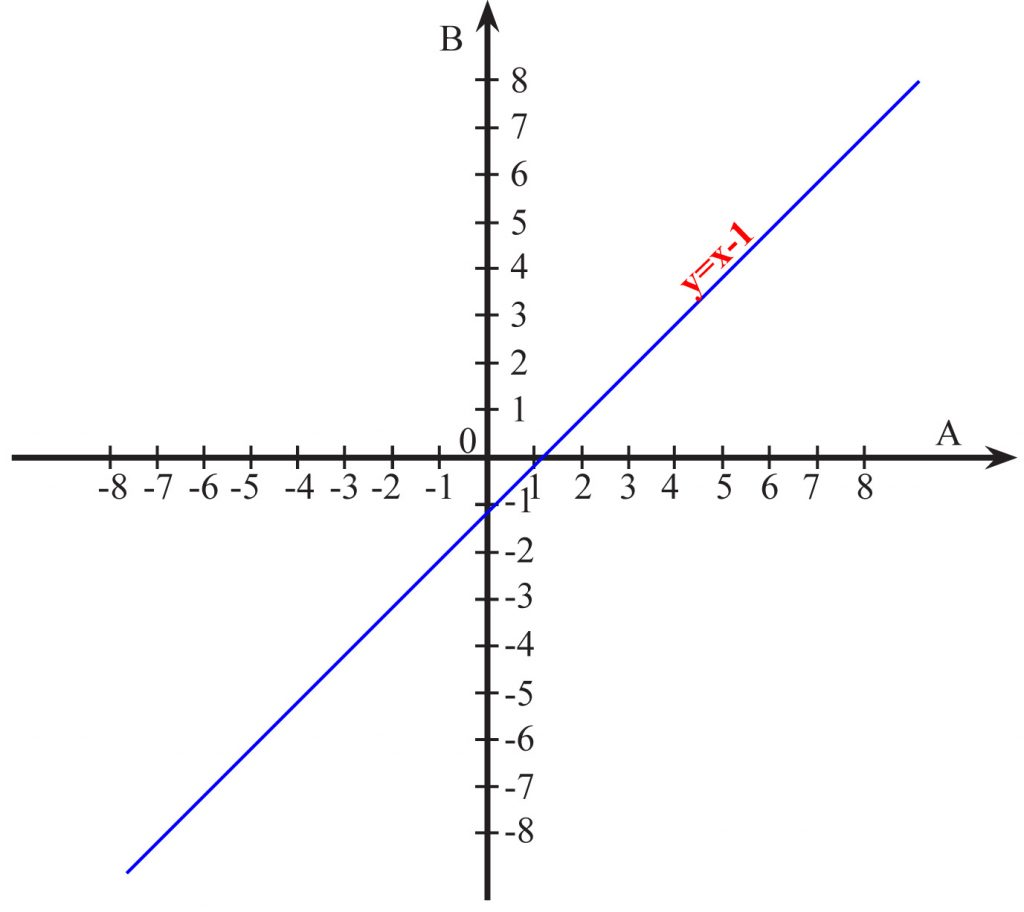
d) y = x – 1 dla x∈R (zbioru liczb rzeczywistych)
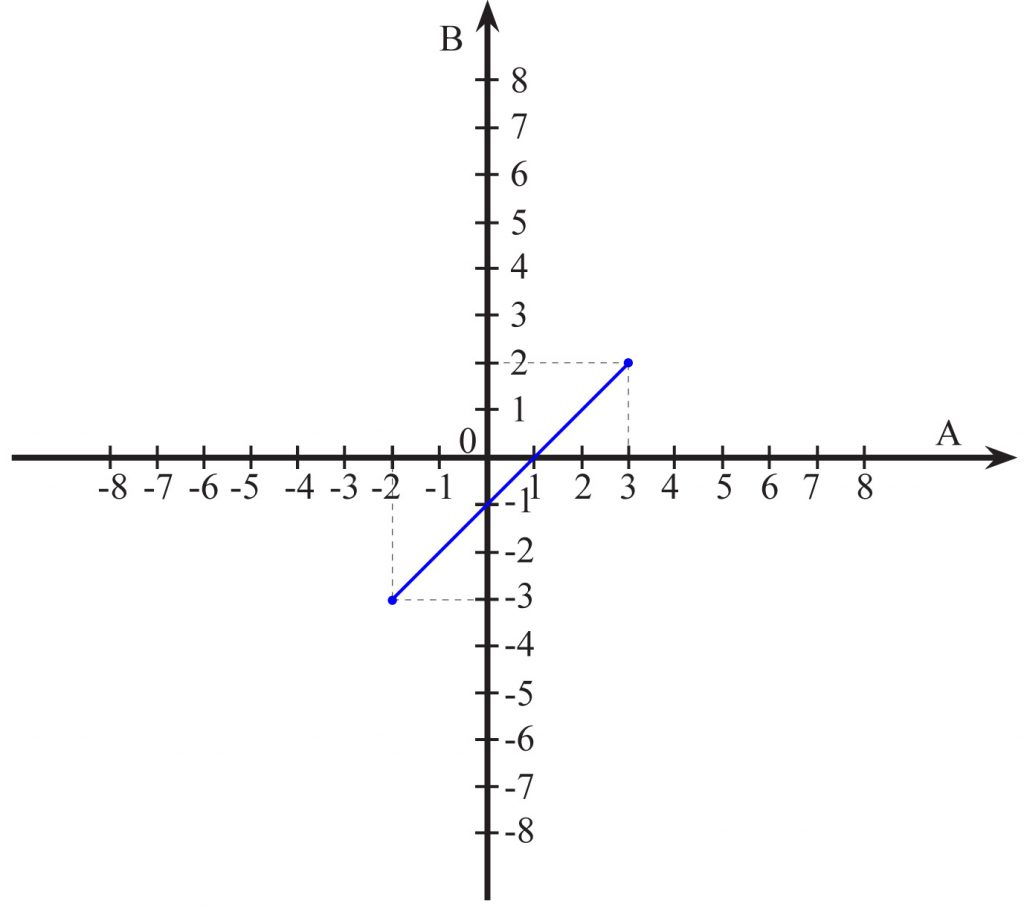
Wykresem jest linia prosta.
e) y = x – 1 dla x∈![]() (x należy do przedziału obustronnie domkniętego od -2 do 3)
(x należy do przedziału obustronnie domkniętego od -2 do 3)
Wykresem jest odcinek, którego końcami są punkty (-2, -3) i (3, 2)
Zapamiętaj!
Wykresem funkcji f na płaszczyźnie z danym układem współrzędnych jest zbiór wszystkich punktów o pierwszej współrzędnej x i drugiej współrzędnej f(x) (czyli y), gdzie x należy do dziedziny funkcji f.