Graniastosłup
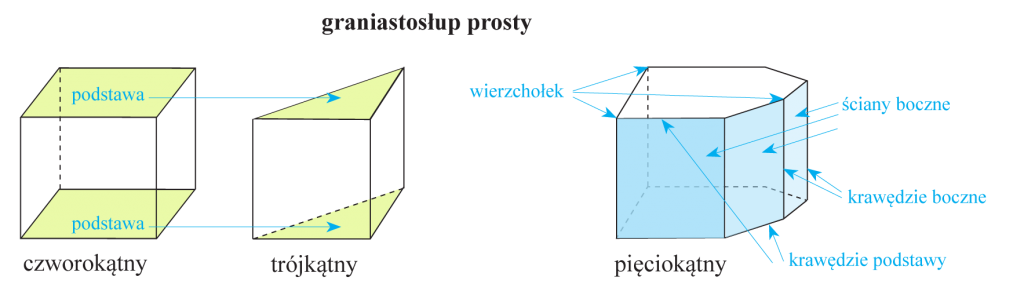
Graniastosłupem nazywamy figurę przestrzenną, której dwie ściany zwane podstawami są przystającymi wielokątami zawartymi w płaszczyznach równoległych, a ściany boczne są równoległobokami.
Uwaga! W graniastosłupie prostym ściany boczne są prostokątami (są prostopadłe do podstaw).
Zapamiętaj!
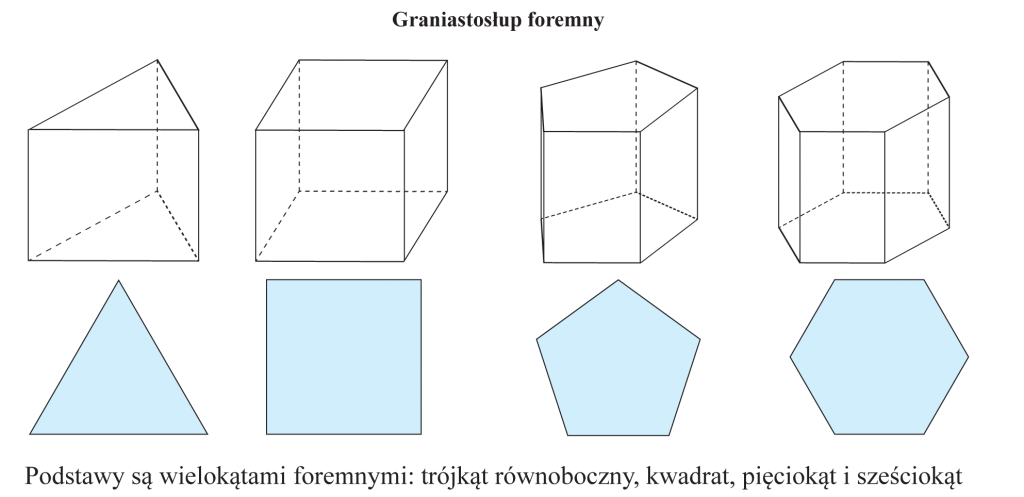
Graniastosłup nazywamy prawidłowym, jeśli jest prosty i podstawy są wielokątami foremnymi.
Wielokątami foremnymi są np. trójkąt równoboczny, kwadrat, sześciokąt foremny.
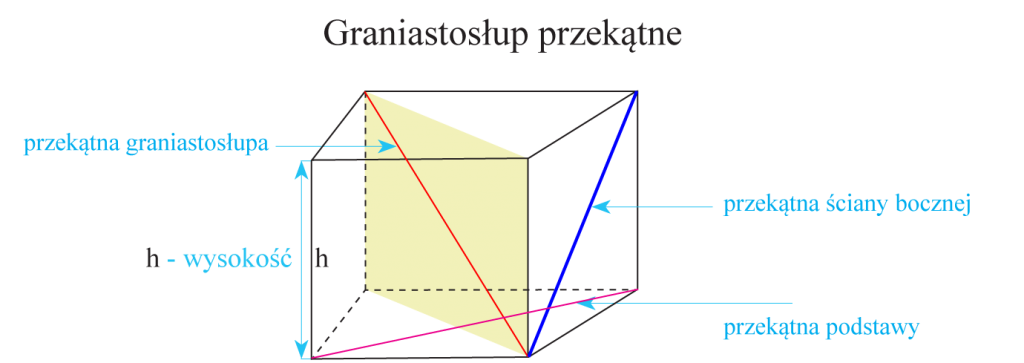
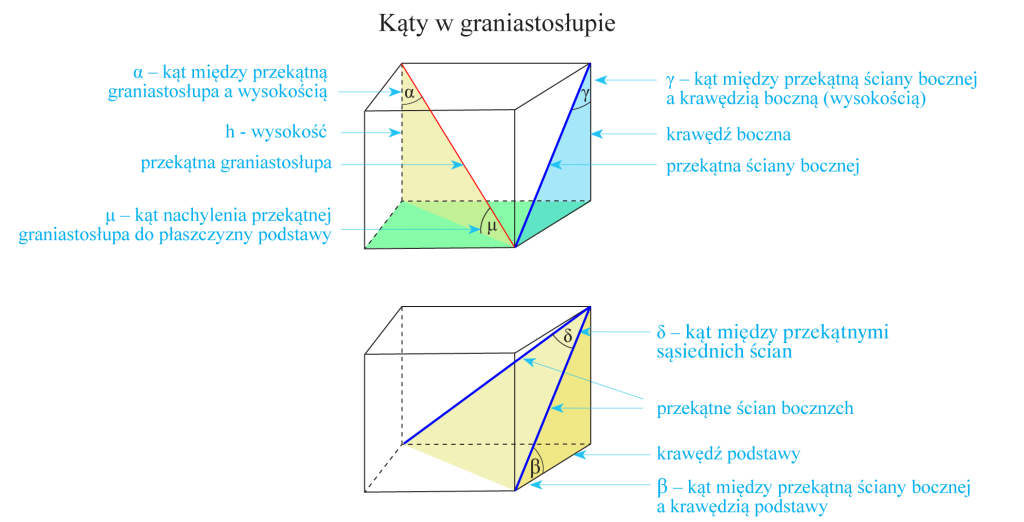
Przekątna graniastosłupa – to odcinek łączący dwa wierzchołki nienależące do płaszczyzny jednej ściany.
Uwaga! Graniastosłup trójkątny ma tylko przekątne ścian bocznych.
Wysokość graniastosłupa – to odcinek prostopadły do podstaw, którego końce leżą na płaszczyznach, w których się te podstawy zawierają.
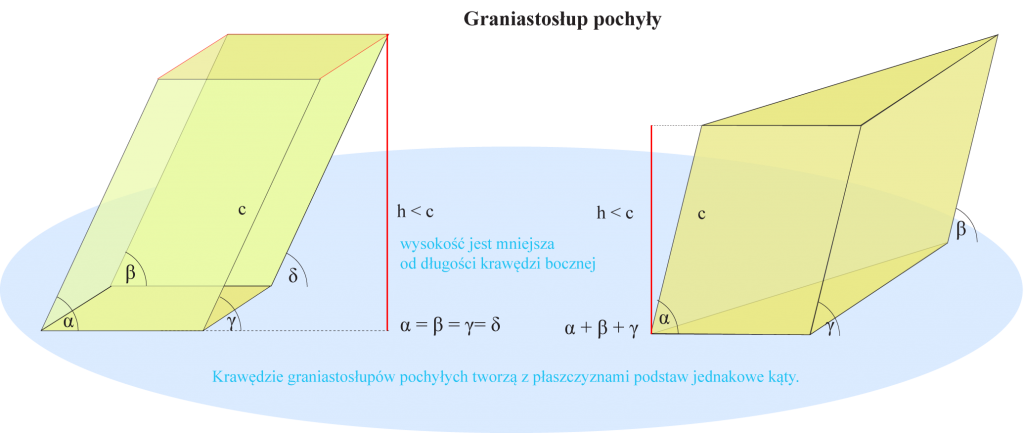
Graniastosłup pochyły to graniastosłup, w którym krawędzie boczne nie są prostopadłe do podstawy.
W graniastosłupie pochyłym długoć wysokoci jest mniejsza od długoci krawędzi bocznej.
Krawędzie graniastosłupów pochyłych tworzą z płaszczyznami podstaw jednakowe kąty.
Pole powierzchni całkowitej graniastosłupa
Objętość graniastosłupa
Prostopadłościan
Prostopadłościan to graniastosłup, którego wszystkie ściany są prostokątami, oraz wszystkie ściany boczne są prostopadłe do podstaw.
W prostopadłościanie dowolne dwie ściany są albo równoległe, albo prostopadłe.
Wysokość graniastosłupa – to odcinek prostopadły do podstaw, którego końce leżą na płaszczyznach, w których się te podstawy zawierają.
Przekątna graniastosłupa – to odcinek łączący dwa wierzchołki nienależące do płaszczyzny jednej ściany.
Wzór na długość przekątnej prostopadłościanu:
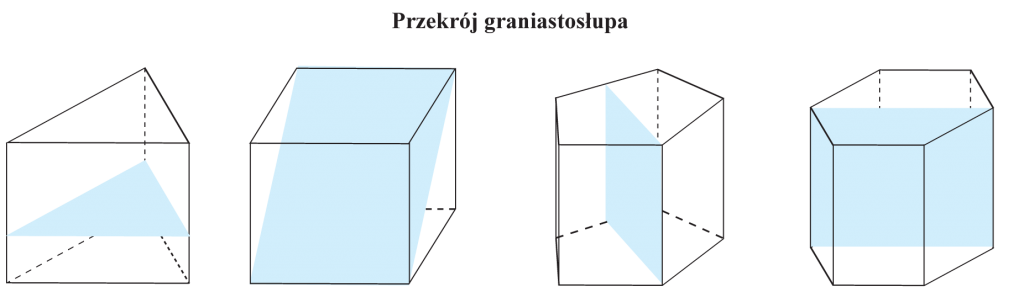
Przekrój graniastosłupa
Przekrojem graniastosłupa nazywamy część wspólną graniastosłupa i płaszczyzny przecinającej ten graniastosłup.
Zadanie 1.
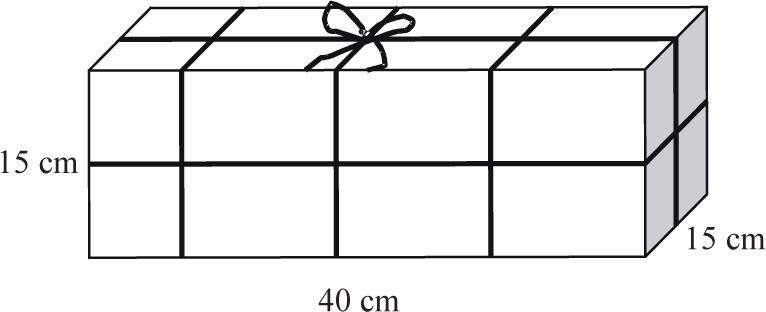
Paczka ma kształt graniastosłupa prawidłowego czworokątnego. Czy na jej obwiązanie wystarczy 4,5 m sznurka, jeżeli na kokardę należy doliczyć 35 cm?
Jak to rozwiązać?
Wystarczy zauważyć, że 4 części sznurka mają długość 40 cm, a części o długości 15 cm jest razem 16. Stąd długość całego sznurka potrzebnego na owinięcie paczki obliczymy, wykonując rachunek (oczywiście, nie można zapomnieć o kokardzie):
4 · 40 cm + 16 · 15 cm + 35 cm = 435 cm = 4,35 m.
Odpowiedź: Ponieważ 4,35 m < 4,5 m, zatem zakupiony sznurek wystarczy na obwiązanie paczki.
Zadanie 2.
Namiot ma kształt graniastosłupa prawidłowego trójkątnego, w którym kąt między przekątną ściany bocznej o długości 3 m, a krawędzią podstawy wynosi 60°. Jaką wysokość ma słupek podtrzymujący konstrukcję namiotu? Przyjmij, że ![]() . Wynik zaokrąglij do części dziesiątych.
. Wynik zaokrąglij do części dziesiątych.