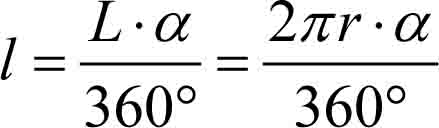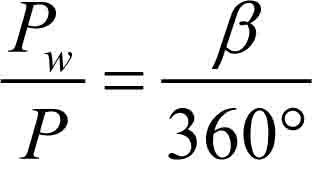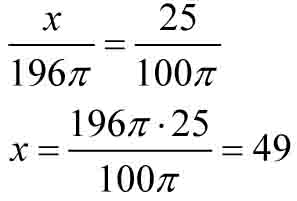Obwód koła
Pole koła
r – długość promienia koła
Uwaga!
Pole i obwód koła są ze sobą ściśle związane: większe pole powierzchni to większy obwód, mniejsze pole to mniejszy obwód.
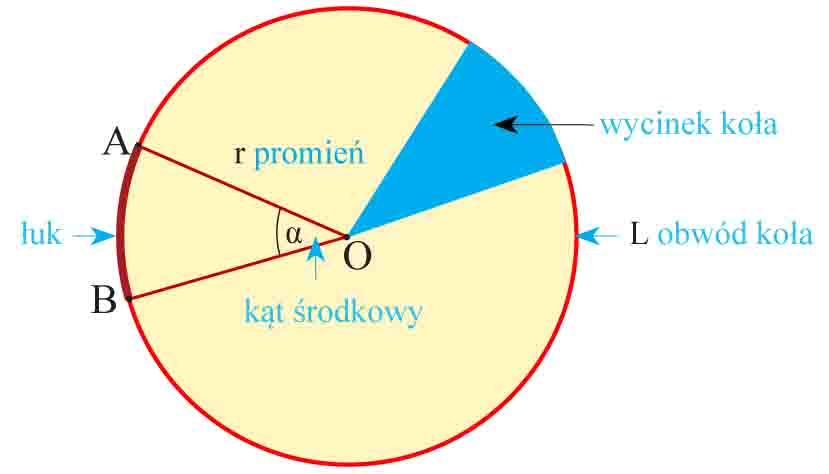
Długość łuku
Łuk jest określony przez promień okręgu r i kąt środkowy α. Długość za-znaczonego łuku AB i obwód okręgu L pozostają
w takim samym stosunku względem siebie jak kąt środkowy i kąt pełny 360°.
Długość łuku wycinka koła o promieniu r wyciętego przez kąt środkowy o mierze α jest równa
Zauważ!
- Łuk okręgu to część całkowitego okręgu. Półokrąg mierzy połowę, czwarta część okręgu mierzy ćwierć długości okręgu.
- Im większy kąt środkowy α, tym dłuższy odpowiadający mu łuk AB.
Pole wycinka koła
Zaznaczonemu na rysunku wycinkowi koła odpowiada kąt środkowy β. Pole tego wycinka koła Pw i pole koła P pozostają w takim samym stosunku względem siebie jak kąt środkowy i kąt pełny 360°.
Pole wycinka koła o promieniu r wyciętego przez kąt środkowy o mierze β jest równe
Zadanie 1
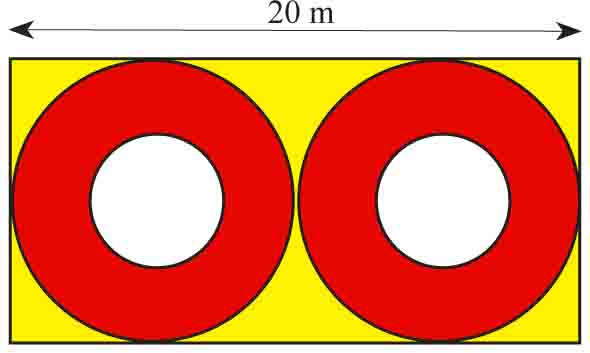
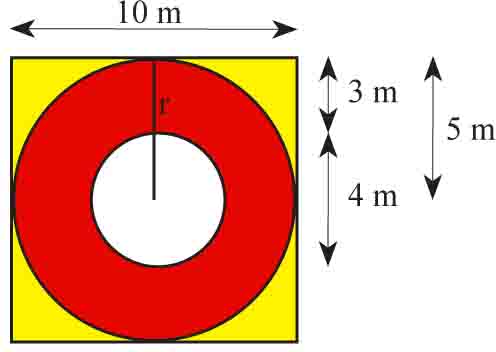
W parku uzdrowiskowym na prostokątnym kwietniku o długości 20 m posadzono kwiaty w trzech kolorach: białym, żółtym i czerwonym (patrz rysunek). Oblicz, jaką powierzchnię zajmują kwiaty koloru czerwonego i żółtego, jeśli kwiatami koloru białego obsadzono 8π m² powierzchni.
Jak to rozwiązać?
Powierzchnia kwietnika składa się z dwóch identycznych elementów. Skoro białe kwiaty zajmują łącznie 8π m², to jeden biały element ma powierzchnię 4π m². Stąd ze wzoru na pole koła P=πr² obliczysz długość promienia białego koła:
πr² = 4π
r² =4
r = 2 [m]
Średnica tego koła ma zatem 4 m.
Ponieważ długość całego kwietnika wynosi 20 m, więc jeden element jest kwadratem o boku 10 m. W element ten wpisane są dwa koła współśrodkowe. Obliczasz teraz szerokość powstałego z czerwonych kwiatów pierścienia kołowego:
Można zatem stwierdzić, że powierzchnię zajmowaną przez czerwone kwiaty wyliczysz, odejmując od pola koła o promieniu 5 m, pole koła zajmowanego przez białe kwiaty:
π· 5² – 4π = 21 [m²]
Kwiaty czerwone zajmują zatem łącznie
2 · 21 = 42 [m²].
Oblicz teraz dla jednego elementu powierzchnię zajmowaną przez kwiaty żółte – musisz odjąć od pola kwadratu pole większego koła.
Otrzymujesz 100 – 25π [m²].
Kwiaty żółte zajmują zatem łącznie
2 · (100 – 25π) = 200 – 50π [m²].
Zadanie 2
Pani Irena rozcięła kawałek tkaniny w kształcie koła o powierzchni 9π dm² na trzy równe części. Każdą z tych części postanowiła obszyć taśmą. Czy na obszycie wystarczy jej 3,6 m taśmy? Przyjmij, że π = 3,14.
Jak to rozwiązać?
Ponieważ pole koła wynosi 9π dm², to po wykorzystaniu wzoru na pole koła otrzymujesz, że r = 3 dm.
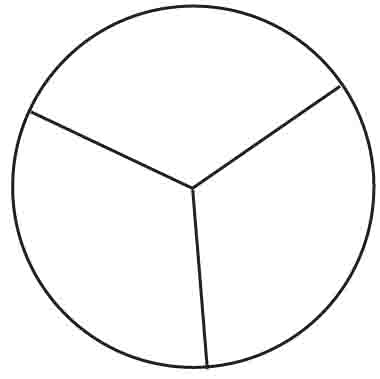
Z treści zadania wynika, że koło zostało podzielone na trzy jednakowe części:
Obwód każdej z tych części wynosi:
r + r + (1/3 · 2πr) = 3 dm + 3 dm + (1/3 · 2 · 3,14 · 3 dm) = =12,28 dm
Odpowiedź. Stąd wynika, że do obszycia trzech części potrzeba 36,84 dm taśmy. Pani Irena ma zatem zbyt mało taśmy na obszycie wszystkich trzech kawałków materiału.
Zadanie 3
Pierścień kołowy wykonany z kolorowego papieru ma pole równe 16π cm², a jego szerokość wynosi 2 cm. Oblicz obwód tego pierścienia kołowego.
Pamiętaj!
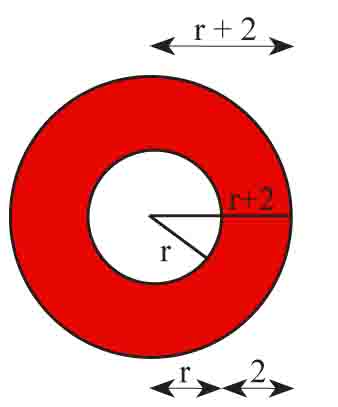
Pierścień kołowy to część płaszczyzny ograniczona dwoma współśrodkowymi okręgami o promieniach R i r, gdzie R > r, wraz z tymi okręgami.
Rozwiązanie
Musisz rozpocząć obliczenia od określenia długości promieni kół, z których powstał pierścień. Pole pierścienia jest różnicą pól tych kół.
π(r + 2)² – πr² = 16π
πr² + 4πr + 4π – πr² = 16π
4πr = 12π
r = 3 [cm]
r + 2 = 5 [cm]
Na obwód pierścienia składa się obwód małego i dużego koła:
(2 · π · 3) + (2 · π · 5) = 16π [cm]
Odpowiedź: Obwód pierścienia wynosi 16 cm.
Sprawdź się przed egzaminem!
Zadanie 1
Mama postanowiła upiec tort urodzinowy. Tort miał średnicę 26 cm, a jego środkowa część o średnicy 14 cm została przyozdobiona startą czekoladą. Oblicz powierzchnię tej części tortu, na której nie ma startej czekolady.
Zadanie 2
Pizza ma kształt koła o średnicy 20 cm, a na jej upieczenie zużyto ok. 25 dag mąki. Ile kilogramów mąki należy wziąć, aby przyrządzić pizzę tej samej grubości, której promień będzie wynosił 14 cm? Zakładamy, że ilość mąki jest wprost proporcjonalna do wielkości pizzy.
Zadanie 3
Rysunki przedstawiają dwie okrągłe monety widziane z boku.
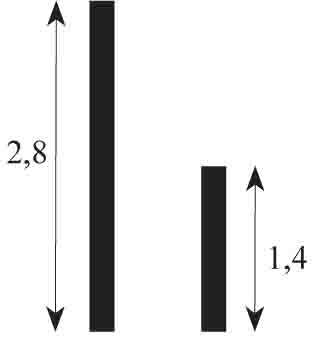
a) Stosunek pól powierzchni większej monety do mniejszej wynosi:
A. 2 : 1
B. 4 : 1
C. 3 : 1
D. 3 : 2
b) Stosunek obwodu mniejszej monety do większej wynosi:
A. 1 : 2
B. 1 : 4
C. 1 : 3
D. 2 : 3
Zadanie 4
Pole koła, w którym kąt środkowy o mierze 45° oparty jest na łuku długości 2π, wynosi:
A. 16
B. 8
C. 64
D. 32
Rozwiązania zadań
Zadanie 1
W tym zadaniu trzeba obliczyć pole pierścienia kołowego! Odejmij od pola koła dużego o promieniu 13 cm pole małego koła o promieniu 7 cm. Otrzymasz: π· 13² – π· 7²= =120 [cm2].
Zadanie 2
Na przyrządzenie większej pizzy potrzeba ok. 0,49 kg mąki.
Komentarz: skoro średnica mniejszej pizzy ma 20 cm, to jej promień wynosi 10 cm. Powierzchnia tej pizzy ma więc 100π [cm²]. Teraz obliczasz pole powierzchni większej pizzy, której promień wynosi 14 cm. Pole to jest równe 196 [cm²].
Po ułożeniu proporcji i wykonaniu obliczeń otrzymujesz odpowiedź:
100π [cm2] — 25 dag
196π [cm2] — x
Zadanie 3:
Odp. a) B, b) A
Zadanie 4:
Odp. C