To jest ważne!
- Rysunki wykonuj bardzo starannie.
- Rysunek nie może być zbyt mały. Lepiej, żeby był duży niż mikroskopijny.
- Nie zakładaj niczego, czego nie wiesz na pewno (np. nie rysuj trójkąta równoramiennego, jeśli nie wiesz, że jest on równoramienny).
- Dobry rysunek ułatwi Ci rozwiązanie zadania, zły – uniemożliwi.
Konstrukcja to opis konstrukcji
Konstrukcja geometryczna to rysunek wykonany za pomocą cyrkla, linijki (bez podziałki) i ołówka. Prawidłowo rozwiązane zadanie konstrukcyjne składa się z opisu konstrukcji i wykonanego zgodnie z tym opisem rysunku. Nawet niezbyt skomplikowane zadanie konstrukcyjne wymaga nakreślenia tak wielu odcinków, łuków i punktów, że bez dokładnego opisu konstrukcji sam rysunek może być nieczytelny. Dlatego prawdziwe jest stwierdzenie, że konstrukcja to w znacznej mierze opis konstrukcji.
Musisz koniecznie umieć… konstruować:
- prostopadłą do danej prostej
- styczną do okręgu
- okrąg wpisany i opisany na trójkącie
- podział odcinka w zadanym stosunku
Zadanie
Dany jest okrąg o nieustalonym środku. Wyznacz konstrukcyjnie ten środek.
Jak rozwiązać takie zadanie?
Zaznaczenie środka „na oko”, po wnikliwym przyjrzeniu się – oczywiście nie wchodzi w grę!
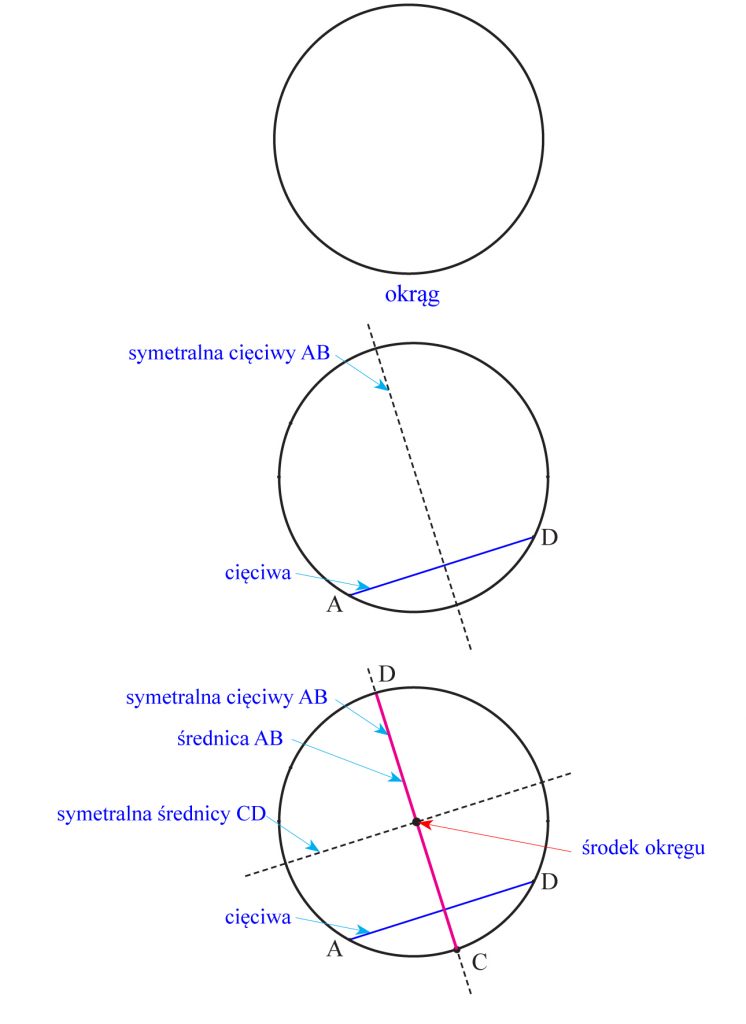
Najpierw wykonaj rysunek okręgu.
Następnie narysuj dowolną cięciwę tego okręgu oraz symetralną tej cięciwy.
Uwaga! Symetralna cięciwy jest prostą zawierającą średnicę tego okręgu.
Środek średnicy CD jest więc środkiem okręgu.
Na egzaminie gimnazjalnym może pojawić się takie zadanie:
Figura złożona z dwóch okręgów nie może mieć:
A. dokładnie jednej osi symetrii;
B. dokładnie dwóch osi symetrii;
C. dokładnie trzech osi symetrii;
D. nieskończenie wielu osi symetrii.
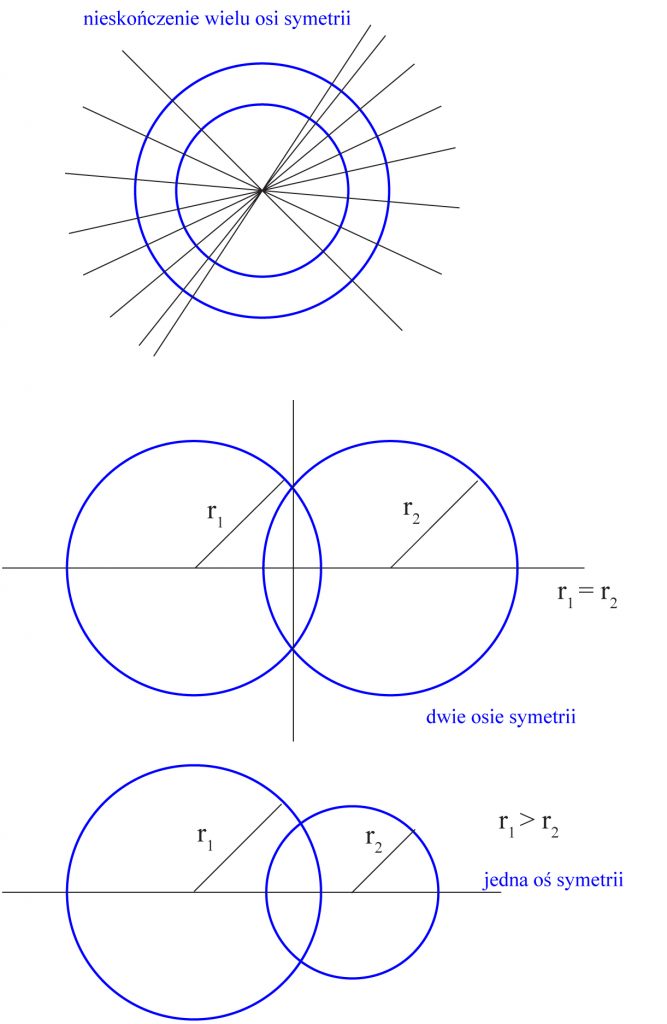
Zadanie nie jest zbyt trudne. Wystarczy zaobserwować, ile osi symetrii może mieć figura złożona z dwóch okręgów. Okręgi mogą mieć:
- Te same środki – wówczas każda prosta przechodząca przez środek tych okręgów jest osią symetrii z nich złożoną.
- Równe promienie i różne środki. Wtedy figura taka ma dokładnie dwie osie symetrii.
- Różne promienie i różne środki. Wtedy istnieje dokładnie jeden środek symetrii takiej figury
Odp. Prawidłowa jest więc odpowiedź C.