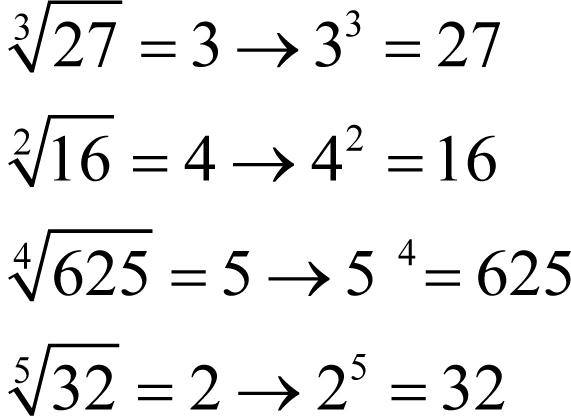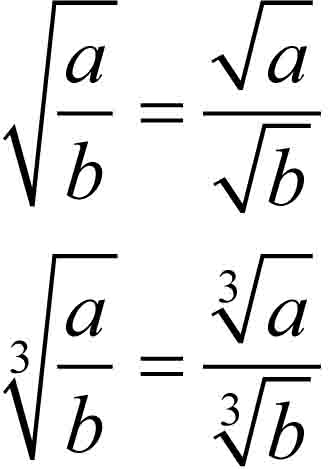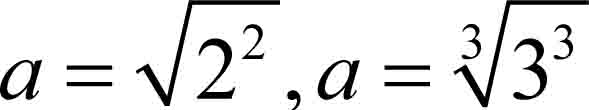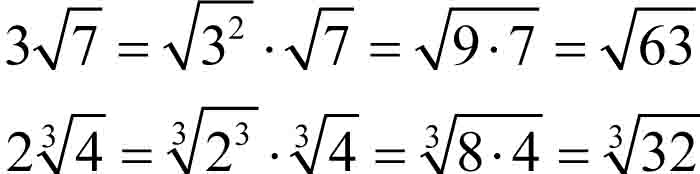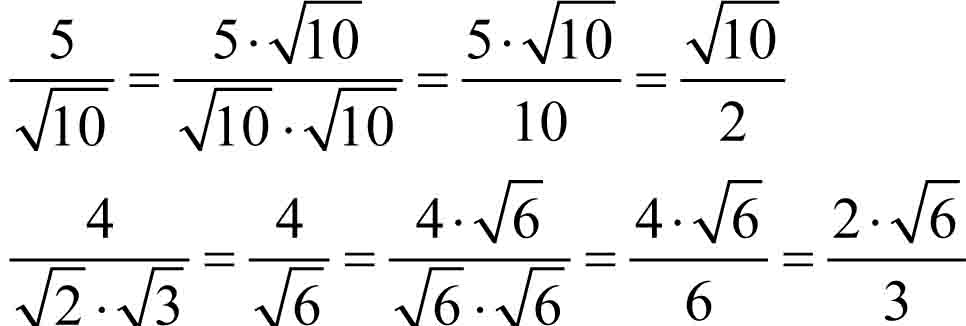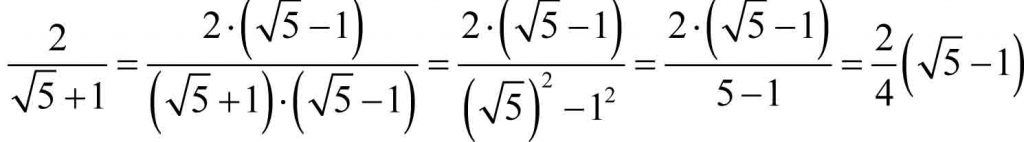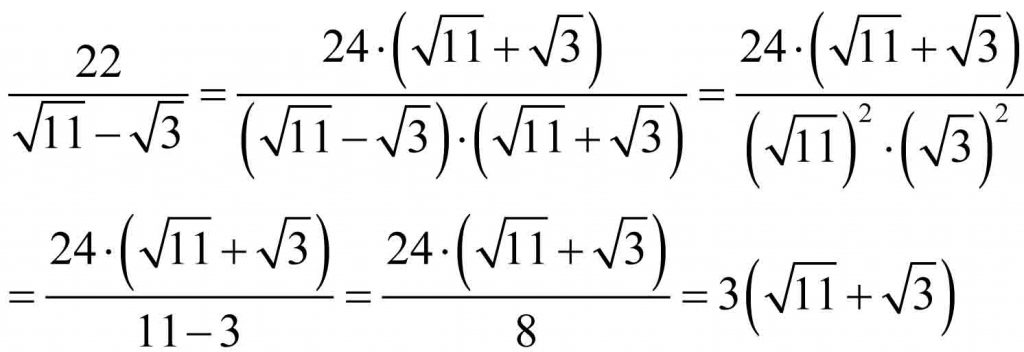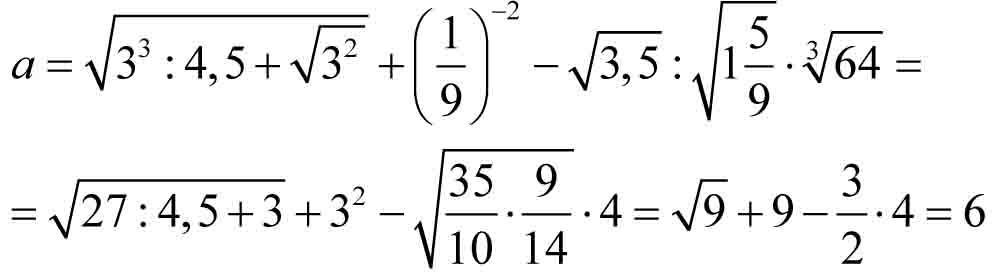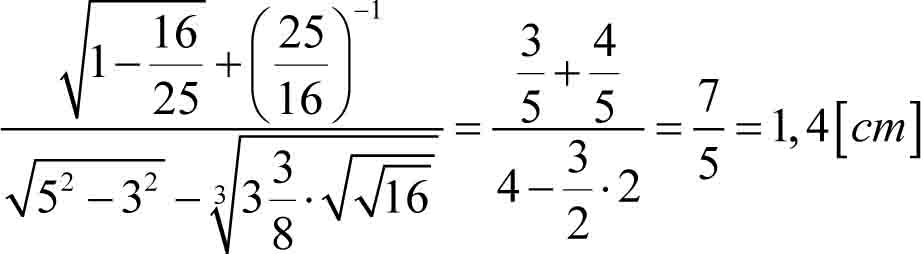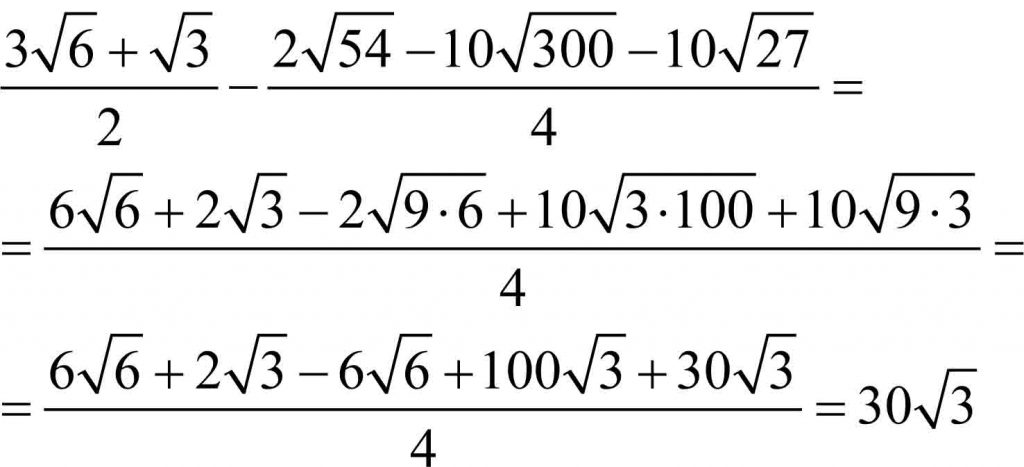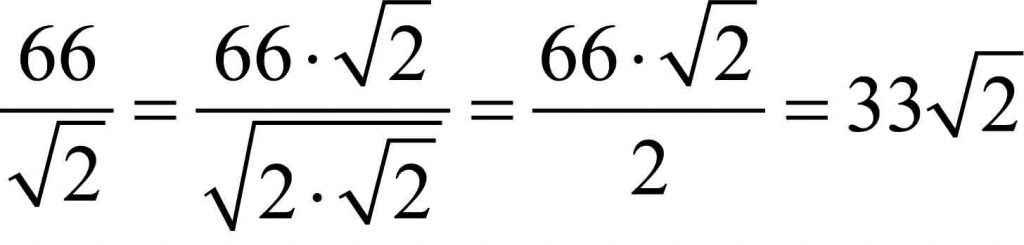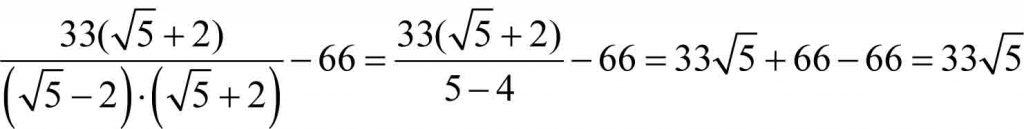Uwaga! Najniższy stopień pierwiastka wynosi 2 i zgodnie z umową, tej dwójki nie piszemy.

  • Pierwiastek, którego stopień wynosi 2, nazywamy pierwiastkiem kwadratowym lub pierwiastkiem stopnia drugiego.
    Arytmetycznym pierwiastkiem drugiego stopnia z liczby nieujemnej a nazywamy taką liczbę nieujemną b, która podniesiona do kwadratu równa jest liczbie podpierwiastkowej a.
  • Pierwiastek, którego stopień wynosi 3, nazywamy pierwiastkiem sześciennym lub pierwiastkiem stopnia trzeciego.
    Arytmetycznym pierwiastkiem trzeciego stopnia z liczby nieujemnej a nazywamy taką liczbę nieujemną b, która podniesiona do sześcianu równa jest liczbie podpierwiastkowej a.

Z definicji pierwiastka kwadratowego i szeœciennego wynika, że:

 

Działania na pierwiastkach

Zapamiętaj twierdzenia dotyczące działań na pierwiastkach.

  • Dla a ≥ 0, b ≥ 0 prawdziwe jest twierdzenie o mnożeniu pierwiastków tego samego stopnia:

  • Natomiast dla a ≥ 0, b > 0 prawdziwe jest twierdzenie o dzieleniu pierwiastków:

  • Częściowe wyciąganie pierwiastka
    W szkole częściej spotkasz się z określeniem wyłączanie czynnika przed znak pierwiastka.
    Polega ono na rozłożeniu liczby podpierwiastkowej na czynniki, z których jeden jest kwadratem liczby całkowitej w przypadku pierwiastka kwadratowego lub sześcianem liczby całkowitej w przypadku pierwiastka sześciennego. Niezbyt jasne – naucz się na przykładzie!


To nie koniec… Zauważcie, że 8 to iloczyn liczb 4 i 2. Zatem przekształcamy dalej:


Całe obliczenie można wykonać szybciej. A jak? A tak: Pamiętaj, że wynik musi być identyczny.

  • Włączanie czynnika pod znak pierwiastka
    Jest to oczywiście operacja odwrotna. Dokonując tego przekształcenia, korzystasz z tego, że

Stąd np.

  • Sumy i różnice pierwiastków
    Dodawać i odejmować pierwiastki wolno tylko wtedy, gdy mają takie same liczby podpierwiastkowe:

Chcąc uprościć zapis pierwiastka, trzeba nieraz zastosować częściowe wyciąganie pierwiastka:

  • Usuwanie niewymierności z mianownika
    Jeżeli mianownik zawiera pierwiastek, to ułamek musimy przekształcić tak, by w mianowniku występowała liczba wymierna. Możemy to zrobić na dwa sposoby:
    1) rozszerzenie – licznik i mianownik mnożymy przez tę samą liczbę różną od zera;
    2) zastosowanie wzoru skróconego mnożenia.

Sprawdź na przykładach!

Licznik i mianownik pomnożono przez pierwiastek występujący w mianowniku!

 

Zastosowano wzór na różnicę kwadratów: (a + b) . (a – b) = a² – b²

Zastosowano wzór na różnicę kwadratów: (a + b) . (a – b) = a² – b²

 

Zadanie 1.

Pan Piotr i pan Adam zaplanowali w swoich ogródkach rabatki kwiatowe o obwodach równych 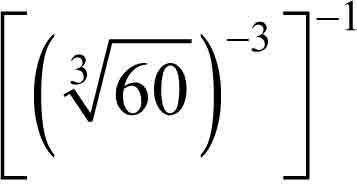m.

Rabatka pana Piotra ma kształt kwadratu, a rabatka pana Adama jest prostokątem, w którym stosunek długości sąsiednich boków wynosi 2 : 3. Który z panów jest właścicielem rabatki o większym polu powierzchni?

Rozwiązanie

Obwody rabatek wynoszą 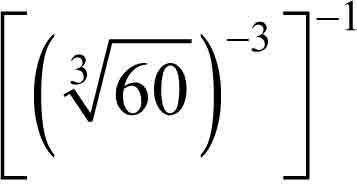m = m = 60 m. Rabatka pana Piotra jest kwadratowa, czyli długość boku wynosi 15 m, a zatem pole ma 225 m². W przypadku rabatki pana Adama można stwierdzić, że na szerokość prostokąta składają się dwie wspólne miary, a na długość trzy wspólne miary – bo stosunek boków wynosi 2 : 3. Zatem obwód składa się z dziesięciu równych miar (zauważ, że prostokąt ma cztery boki, po dwa równej długości). Wspólna miara wynosi więc 60 m : 10 = 6 m, czyli długość boku prostokątnej rabatki jest równa 18 m, a szerokość 12 m. Stąd pole tej rabatki jest równe 216 m². Większą powierzchnię ma rabatka pana Piotra.

Zadanie 2.

Sznur korali składa się ze stu kulistych koralików. Siedemdziesiąt z nich ma promień o długości a milimetrów, natomiast pozostałe mają średnicę dwa razy mniejszą od średnicy większych korali. Jaka może być najmniejsza długość tego sznura korali, jeżeli:

Rozwiązanie:
Oblicz najpierw promień dużego koralika:

Z tego wynika, że średnica tego koralika wynosi 1,2 cm, a ponieważ dużych korali jest 70, więc tworzą one sznur o długości 84 cm.
Zgodnie z warunkami zadania pozostałe koraliki są mniejsze – ich średnice wynoszą 1,2 : 2 = 0,6 cm. Stąd 30 małych koralików tworzy sznur o długości 18 cm. Otrzymujemy zatem najmniejszą długość sznura korali, która jest równa 1,02 m.

Zadanie 3.

Na mapie sporządzonej w skali 1 : 200 000 odległość między miastami A i B wynosi:

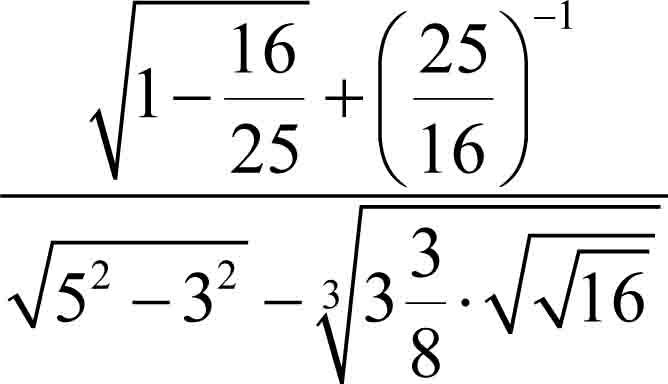
centymetrów. Ile kilometrów w rzeczywistości ma ta odległość?

Rozwiązanie
Odległość na mapie wynosi.

Ponieważ 1,4 cm . 200 000 = 280 000 cm, czyli szukana odległość w rzeczywistości wynosi 2,8 km.

Zadanie 4.

Ula, Hania i Renata uszyły z płótna proporczyki w kształcie trójkątów równoramiennych, w których podstawy są równe i mają długość 20 cm. Która z dziewczynek potrzebowała do uszycia proporczyka najwięcej, a która najmniej materiału, jeżeli wysokość opuszczona na podstawę w proporczyku Uli ma długość 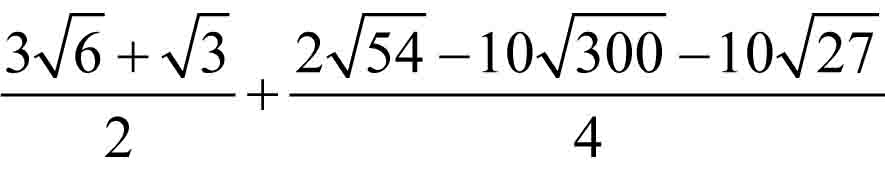cm, w proporczyku Hani cm, a w proporczyku Renaty cm?

Rozwiązanie
Zauważ! W tym zadaniu nie musimy liczyć pól powierzchni proporczyków. Ponieważ podstawy trójkątów są identyczne, wystarczy określić długości wysokości trójkątów – im dłuższa wysokość trójkąta, tym większe pole podstawy.
Oblicz zatem, który z proporczyków ma największą, a który najmniejszą wysokość.
Proporczyk Uli:

Proporczyk Hani:

Proporczyk Renaty:

Ponieważ 33√5 > 33√3 > 33√2, zatem najwięcej płótna potrzebowała Renata, a najmniej Hania.