Podstawowe konstrukcje geometryczne

Zadanie 1
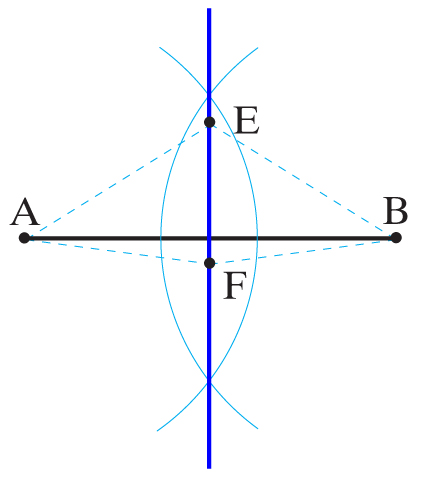
Dany odcinek AB podziel konstrukcyjnie na połowy.

Opis:
Z punktów A i B zataczamy łuki dowolną, ale jednakową rozwartością cyrkla aż do przecięcia się w punktach C i D, które łączymy otrzymując prostą zwaną symetralną odcinka AB. Symetralna w przecięciu z odcinkiem AB tworzy punkt K, który jest jego środkiem. Punkty symetralnej odcinka posiadają tę własność, że ich odległość od końców danego odcinka jest jednakowa, i tak:

|AK| = |KB| ; |AE| = |EB| ; |AD| = |DB| ; |AC| = |CB| ; |AF| = |FB|

Symetralna odcinka jest więc prostą prostopadłą do danego odcinka i dzielącą go na połowy.
Uwaga: korzystając z konstrukcji symetralnej można odcinek podzielić na 2, 4, 8, 16 … tzn 2n (n – liczba naturalna) części.

Zadanie 2
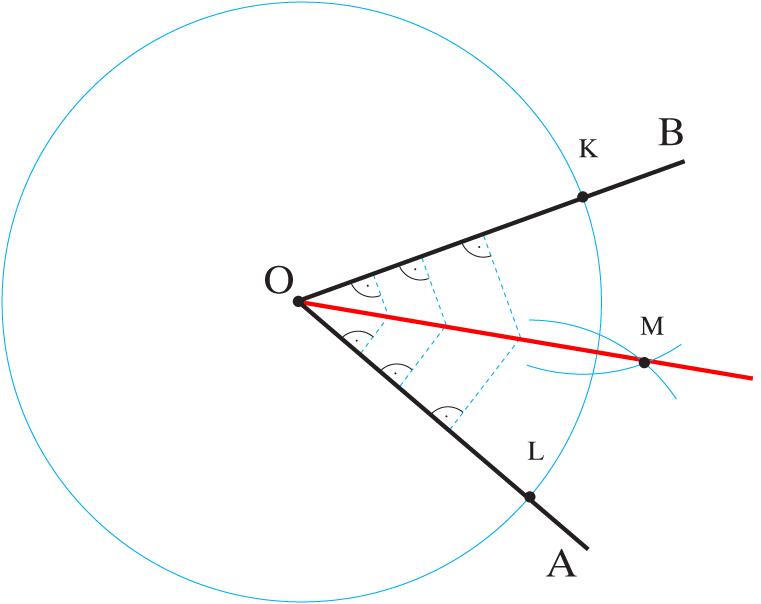
Dany kąt AOB podziel konstrukcyjnie na połowy.

1)
Z punktu O zataczam łuk dowolnym promieniem.
Co otrzymuję?
Punkty K i L przecięcia łuku z ramionami kąta.

2)
Z punktów K i L zataczam łuki dowolnym ale jednakowym promieniem
Co otrzymuję?
W przecięciu łuków punkt M.

3)
Łączę punkty O i M.
Co otrzymuję?
Półprostą dzielącą kąt na połowy. Półprostą dzielącą kąt na połowy nazywamy dwusieczną.

Punkty należące do dwusiecznej są równoodległe od ramion danego kąta.

Uwaga

• Odległość powinna kojarzyć się z prostopadłością.
• Korzystając z konstrukcji dwusiecznej, można kąt podzielić na 2, 4, 8, 16, … tzn 2n (n – liczba naturalna) części.

Zadanie 3:
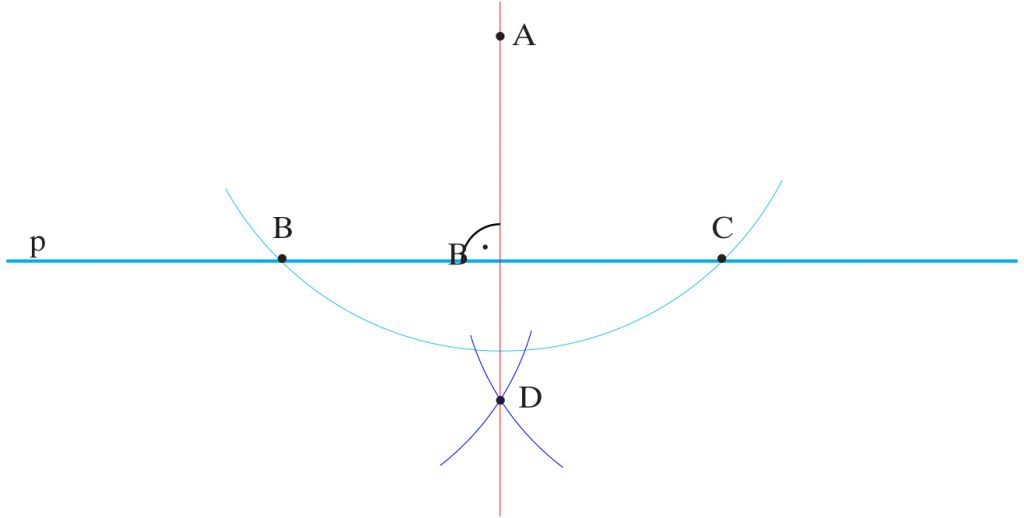
Dana jest prosta p i punkt A nie należący do niej. Poprowadzić przez punkt A prostopadłą do danej prostej p.

Co kreślę
1) Z punktu A zataczam łuk dowolnym promieniem
Otrzymuję punkty B i C przecięcia łuku z prostą p.
2)
Z punktów B i C zataczam jednakowym promieniem łuki do przecięcia się
Otrzymuję punkt D.
3)
Łączę punkty A i D Prostą AD prostopadłą do p

Zadanie 4
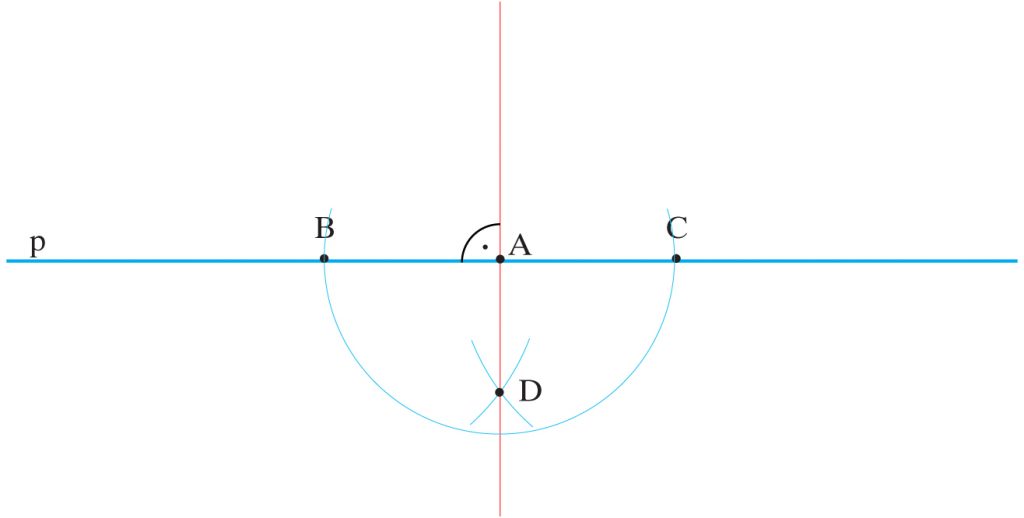
Dana jest prosta p i punkt A należący do niej. Poprowadzić przez punkt A prostopadłą do danej prostej.

Opis jak wyżej.
Uwaga: Zauważyć należy, że do rozwiązania zadania 3 i 4 posłużyliśmy się konstrukcją symetralnej odcinka.

Zadanie 5
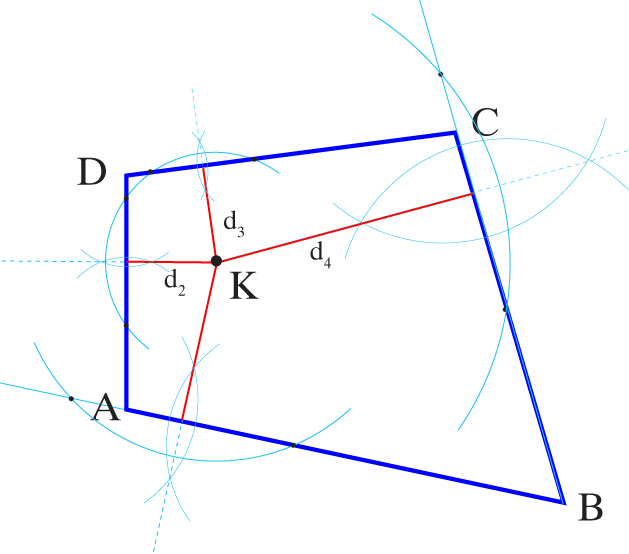
Dany jest czworokąt ABCD i punkt K leżący na jego płaszczyźnie. Znajdź konstrukcyjnie odległość punktu K od każdego boku tego czworokąta.

Długości odcinków: d1, d2, d3, d4 są szukanymi odległościami.
Uwaga: posłużyliśmy się tutaj kreśleniem prostopadłej do danej prostej z punktu K nie leżącego na tej prostej (zadanie 3).

Zadanie 6
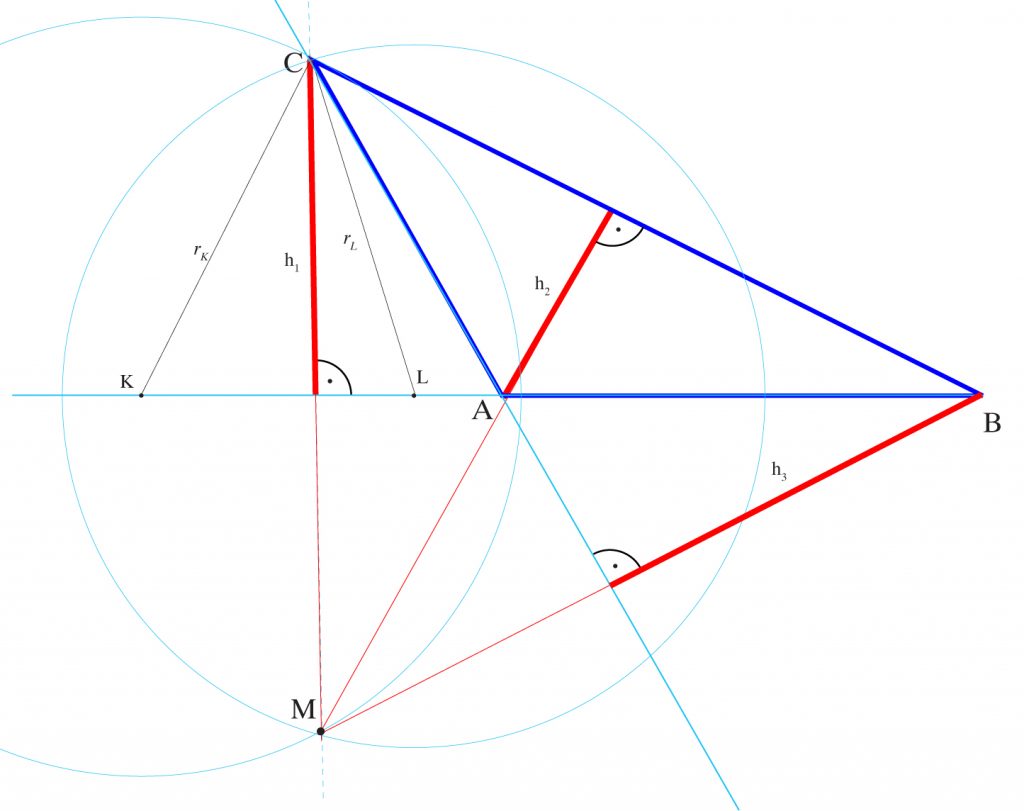
Nakreśl konstrukcyjnie wysokości trójkąta:

• a) ostrokątnego
• b) prostokątnego
• c) rozwartokątnego.

Wysokość trójkąta jest to najkrótszy odcinek łączący jeden z wierzchołków trójkąta z prostą zawierającą przeciwległy bok trójkąta, zwany podstawą. Wysokość jest zawsze prostopadła do podstawy.
a)

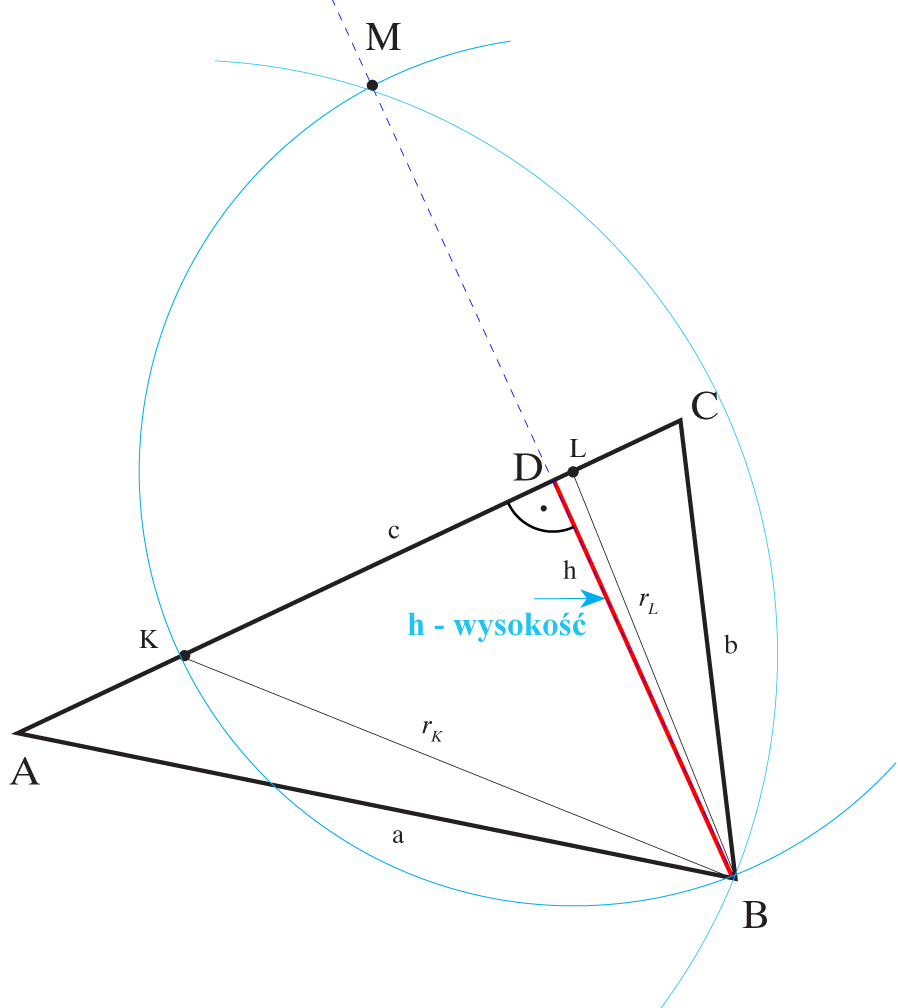
1. Na boku (podstawie) trójkąta wyznaczamy dwa dowolne punkty np. K, L.
2. Z punktu K rysujemy łuk o promieniu rk równym odległości punktu K od wierzchołka trójkąta B.
2. Z punktu L rysujemy łuk o promieniu rL równym odległości punktu L od wierzchołka trójkąta B.
3. Punkt przecięcia łuków M łączymy prostą z wierzchołkiem trójkąta B. Odcinek BD leżący na tej prostej jest wysokością h.

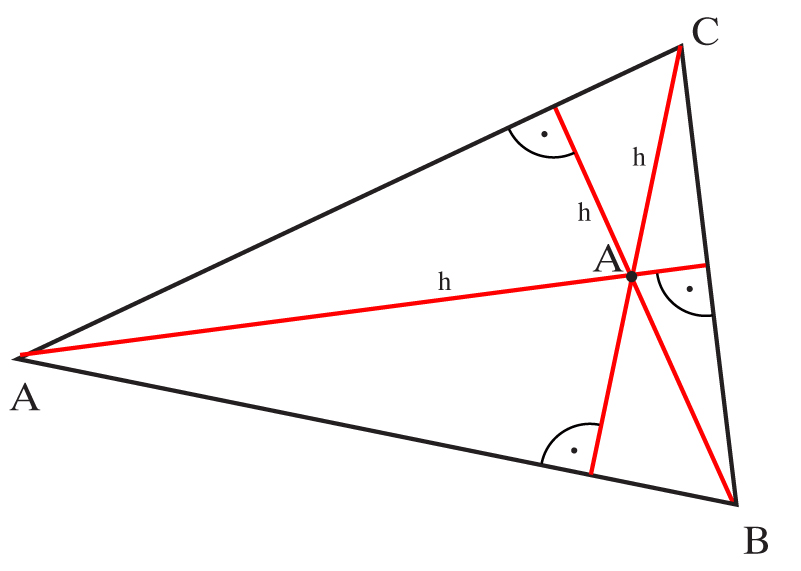
Każdy trójkąt ma trzy wysokości, które przecinają się w jednym punkcie, który leży na płaszczyźnie trójkąta.

 

b)

Wierzchołek A jest punktem przecięcia się wysokości trójkąta prostokątnego.

c)

Punkt M jest punktem przecięcia się przedłużeń wysokości trójkąta rozwartokątnego (leży poza płaszczyzną trójkąta)

Zadanie 7
Opisz okrąg na trójkącie:

a) ostrokątnym
b) prostokątnym
c) rozwartokątnym

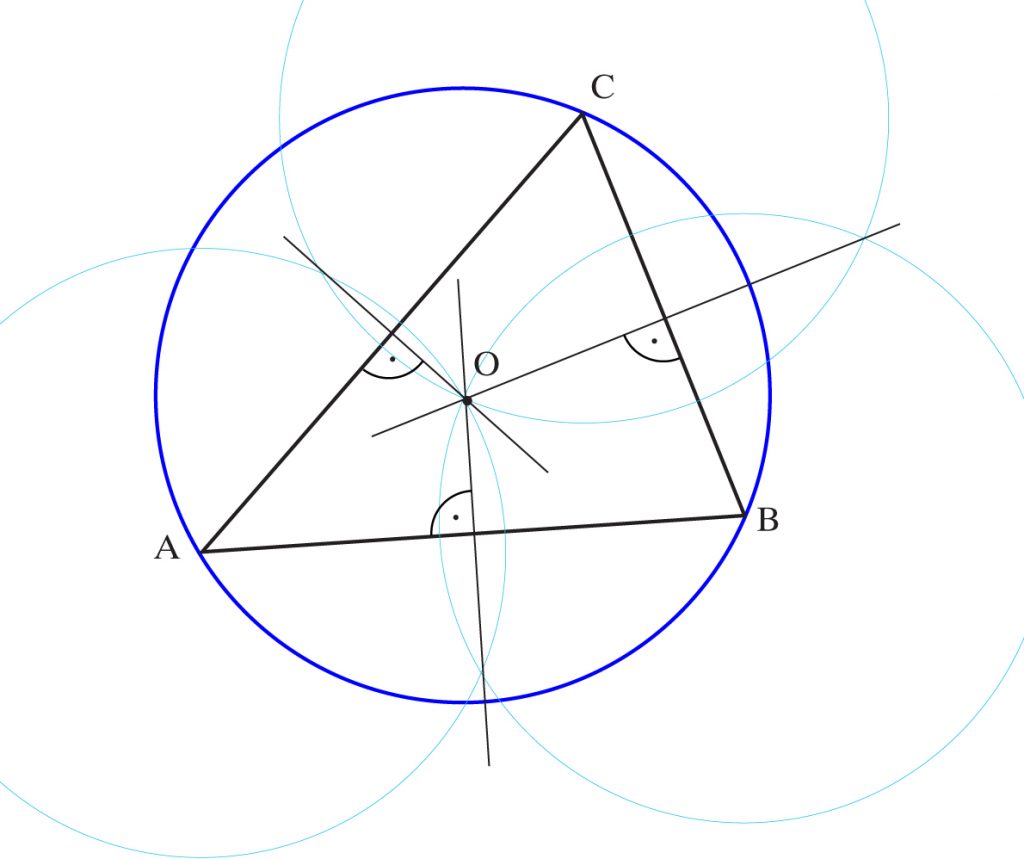
Uwaga! Okrąg jest opisany na wielokącie wtedy, gdy wszystkie wierzchołki tego wielokąta należą do okręgu.
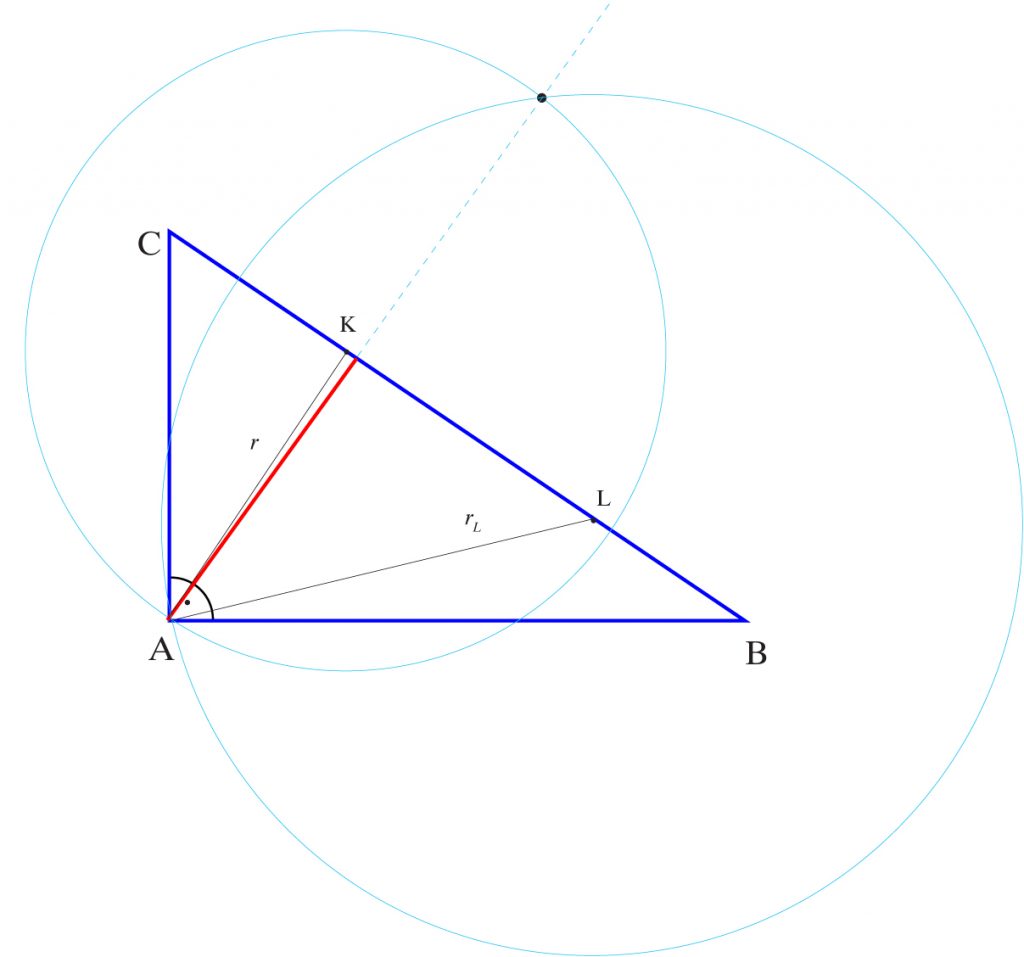
Środek okręgu opisanego leży na przecięciu symetralnych boków trójkąta.

a) Środek okręgu opisanego na trójkącie ostrokątnym leży wewnątrz tego trójkąta.

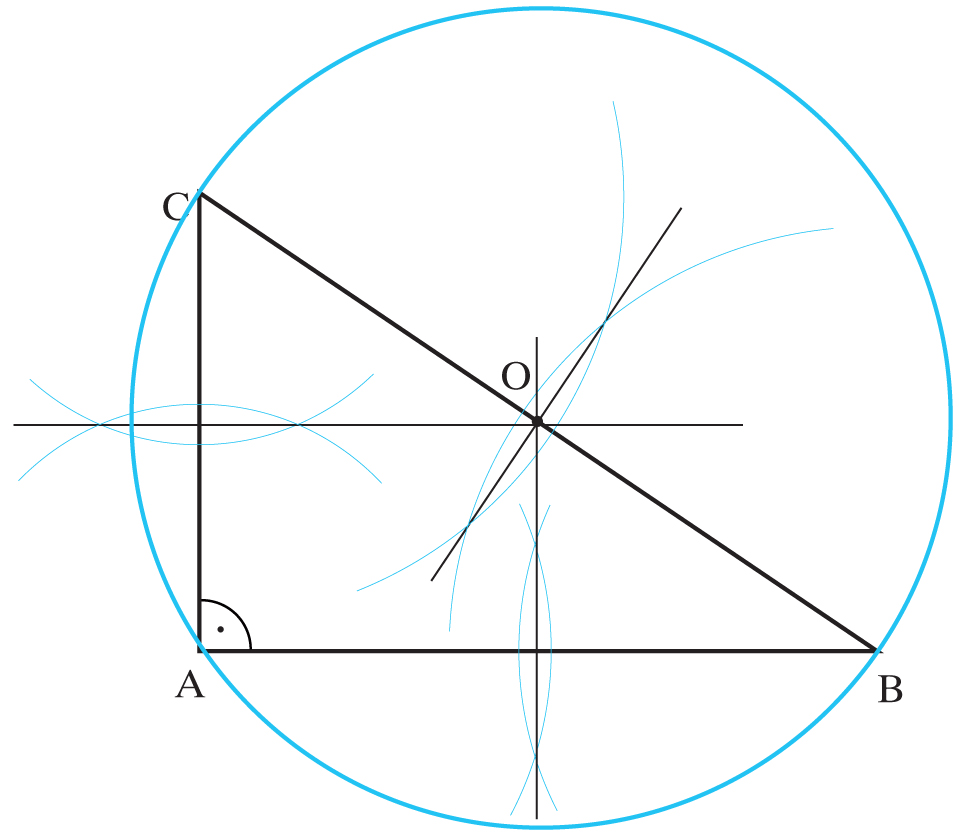
b) Środek okręgu opisanego na trójkącie prostokątnym leży w połowie przeciwprostokątnej.

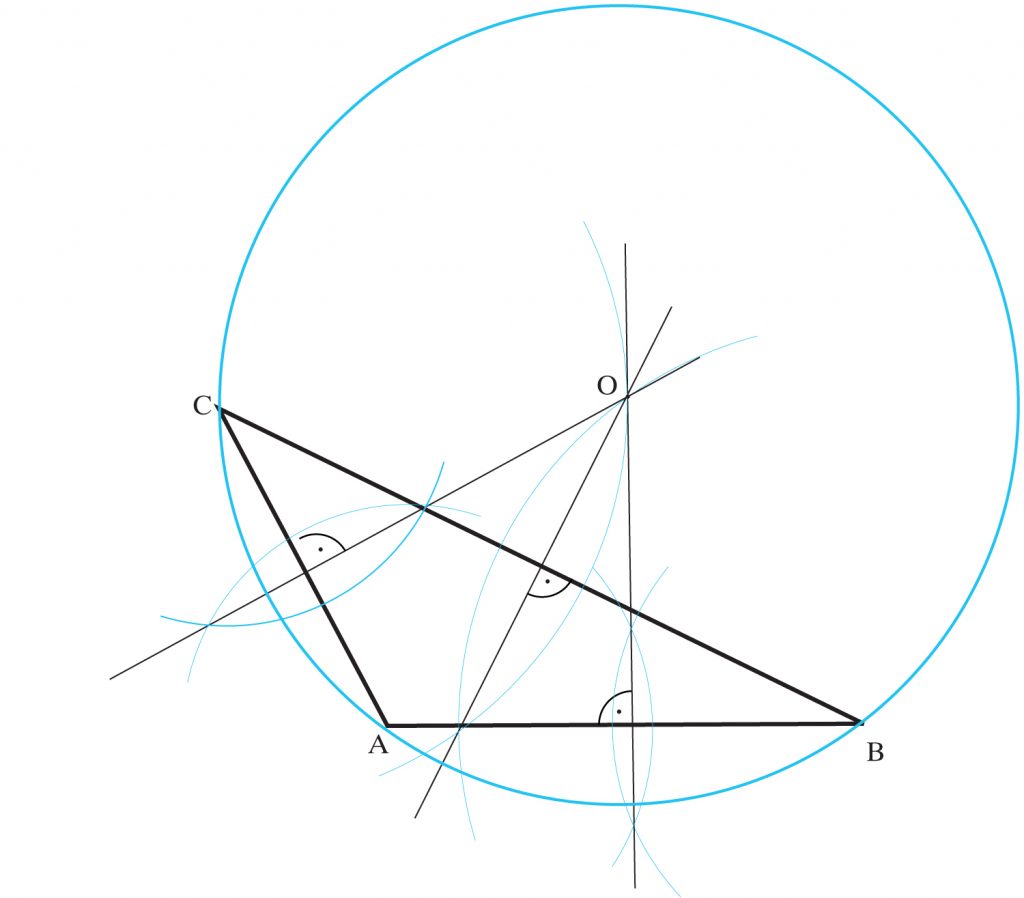
c) Środek okręgu opisanego na trójkącie rozwartokątnym leży poza płaszczyzną trójkąta.

Uwaga: Posłużono się tu konstrukcją symetralnej odcinka.
Środek okręgu opisanego na trójkącie leży w przecięciu symetralnych jego boków.

Zadanie 8
Na każdym z podanych czworokątów opisz okrąg:

a) prostokąt
b) kwadrat
c) romb
d) równoległobok
e) trapez różnoboczny
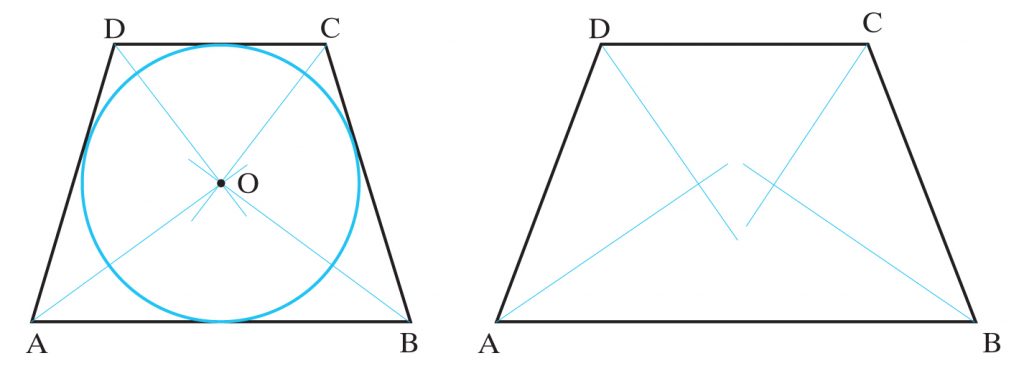
f) trapez równoramienny
g) trapez prostokątny

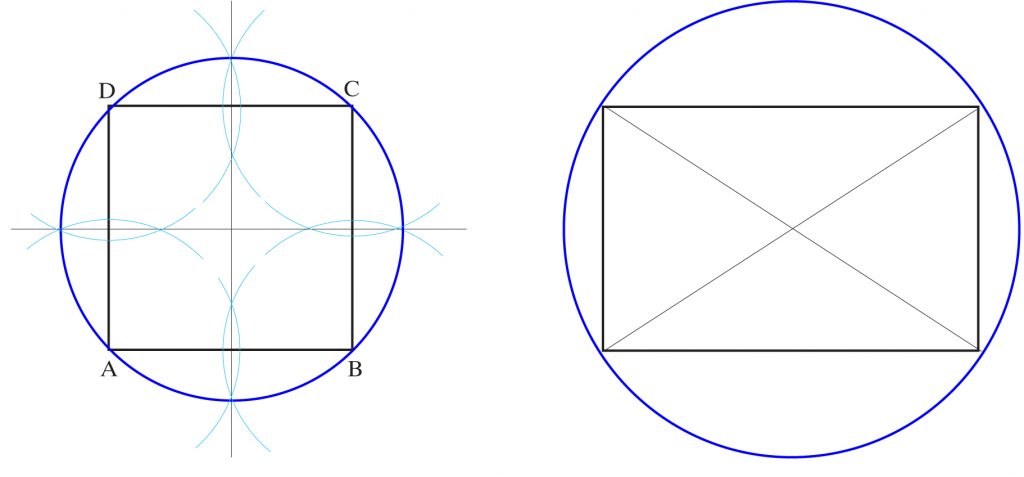
a) b)

Środek okręgu opisanego na prostokącie lub kwadracie leży w punkcie przecięcia się przekątnych. (Jest to również punkt przecięcia się symetralnych wszystkich boków prostokąta lub kwadratu).

c) d)
Na rombie i równoległoboku nie da się opisać okręgu, gdyż symetralne boków nie przecinają się w jednym punkcie. Nie można wyznaczyć środka okręgu.

e)
Na trapezie różnobocznym nie da się opisać okręgu, gdyż symetralne jego boków nie przecinają się w jednym punkcie.

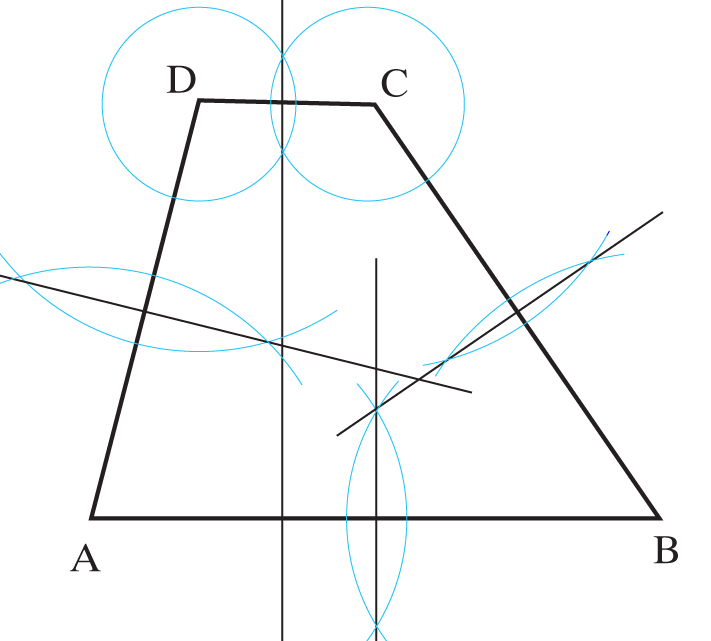
f)
Środek okręgu opisanego na trapezie równoramiennym leży w punkcie przecięcia się symetralnych jego boków.

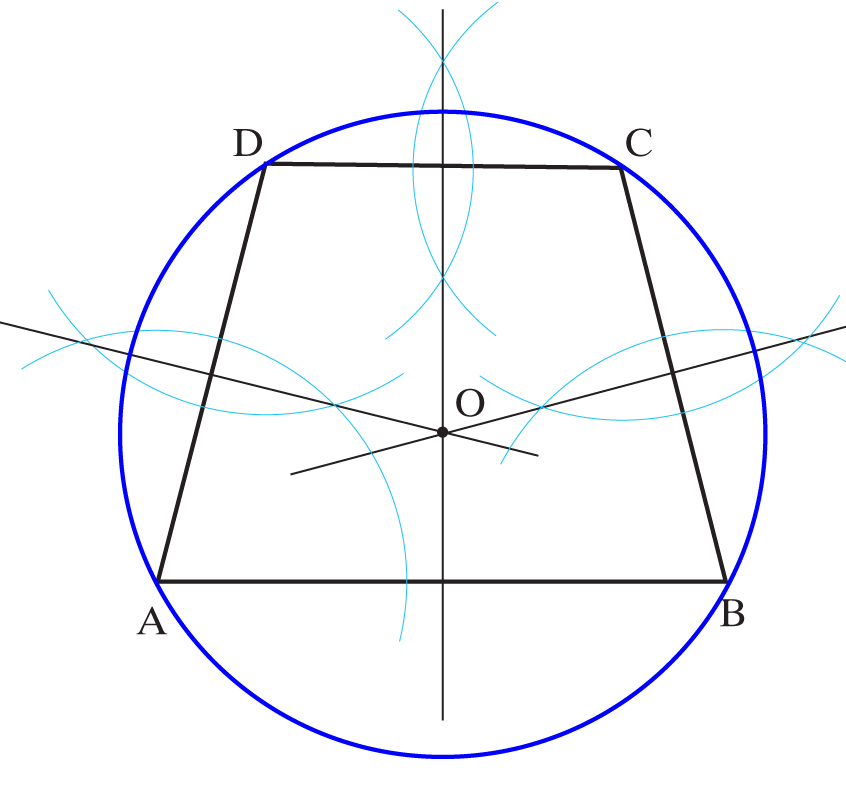
g)
Na trapezie prostokątnym nie da się opisać okręgu, gdyż symetralne jego boków nie przecinają się w jednym punkcie.

Uwaga: Aby na czworokącie dało się opisać okrąg, sumy jego kątów przeciwległych muszą być równe.

Zadanie 9
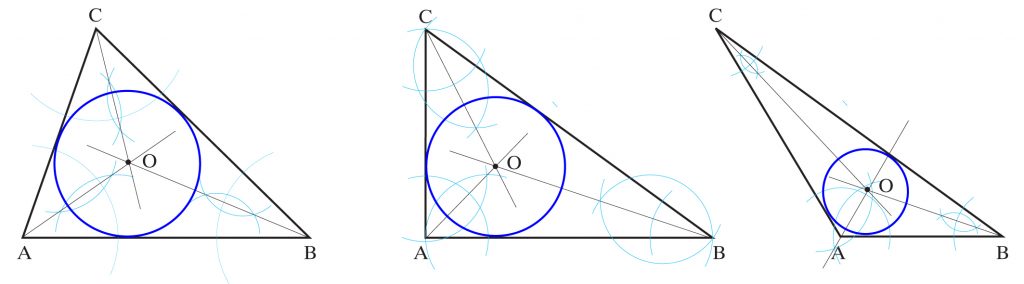
Wpisz okrąg w trójkąt:

a) ostrokątny
b) prostokątny
c) rozwartokątny

Okrąg nazywamy wpisanym w wielokąt wtedy, gdy wszystkie boki tego wielokąta są styczne do danego okręgu.
Aby wpisać okrąg w wielokąt należy wykreślić dwusieczne kątów tego wielokąta.

a) b) c)

Zadanie 10
Wpisz okręgi w następujące czworokąty:

a) kwadrat
b) romb
c) równoległobok
d) prostokąt
e) trapez równoramienny
f) trapez prostokątny

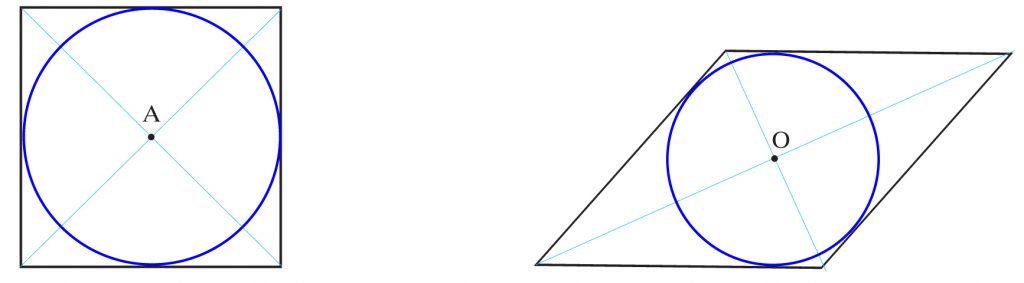
a) b)

W kwadracie i rombie środek okręgu wpisanego leży w przecięciu się przekątnych.

c) d)
Dwusieczne kątów prostokąta i równoległoboku nie przecinają się w jednym punkcie. W te czworokąty nie da się wpisać okręgu.

e)
Tylko w niektóre trapezy równoramienne można wpisać okrąg.

f)

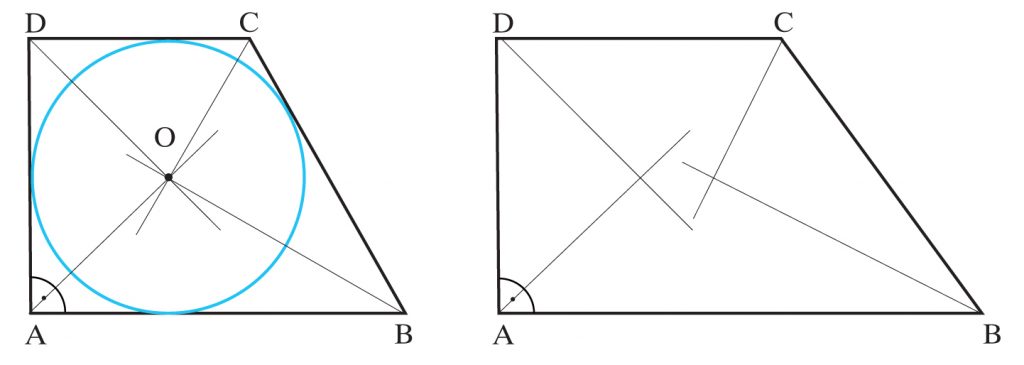
Tylko w niektóre trapezy prostokątne można wpisać okrąg.

Uwaga:
Okrąg da się wpisać w taki czworokąt, w którym sumy przeciwległych boków są równe.

Zadanie 11:
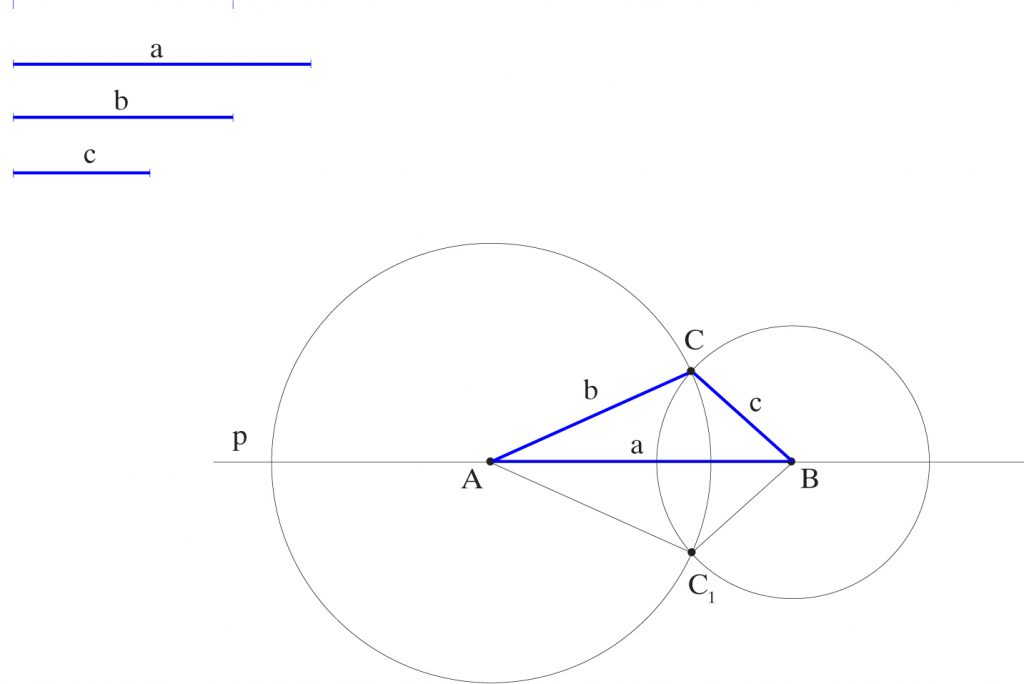
Zbuduj trójkąt, mając dane trzy jego boki.

Opis:

1) Na prostej p od punktu A odkładam odcinek a. Otrzymuję punkt B.

2) Z punktu A jako ze środka zataczam okrąg promieniem b.

3) Z punktu B jako ze środka zataczam okrąg promieniem c.
W ten sposób otrzymuję punkty C i C’ w miejscach przecięcia okręgów.

4) Łączę punkt C z punktami A i B oraz punkt C’ z punktami A i B. Otrzymuję trójkąty ABC i ABC’.

Uwaga: Mamy 2 rozwiązania zadania: trójkąt ABC i trójkąt ABC’, które są przystające.
Badanie rozwiązalności: Zadanie ma rozwiązanie, gdy spełniony jest warunek:
a < b + c
b < a + c
c < a + b

Trójkąty są przystające jeśli mają odpowiednie boki równe.

Zadanie 12
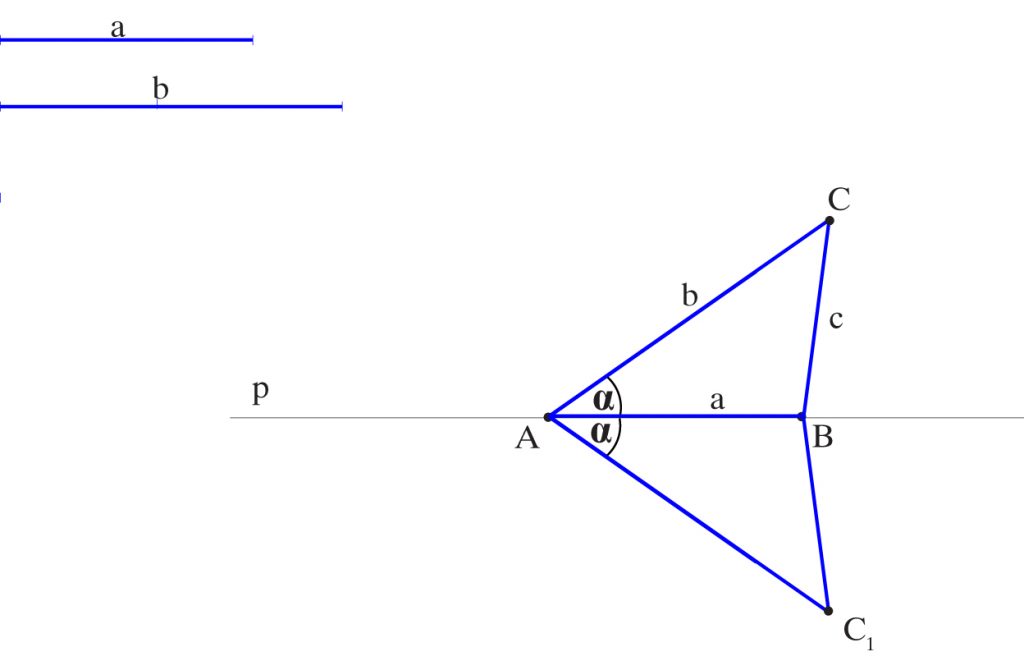
Zbuduj trójkąt mając jego dwa boki a i b, oraz kąt zawarty między tymi bokami.

Opis:

1) Na prostej p odkładam od punktu A odcinek a. Otrzymuję punkt B.

2) Przenoszę kąt tak aby jego wierzchołkiem był punkt A i jednym ramieniem prosta p. W ten sposób otrzymuję drugie ramię kąta (jedno nad prostą p a drugie pod prostą p).

3) Na drugim ramieniu kąta odkładam od wierzchołka A odcinek b. Uzyskuję punkty C i C’.

4) Łączę punkt C z punktem B (oraz punkt C’ z punktem B). Trójkąt ABC
Trójkąt ABC’

Otrzymujemy w rozwiązaniu 2 trójkąty ABC i ABC’, które są przystające.

Badanie rozwiązalności: kąt może być ostry, prosty lub co najwyżej rozwarty.
Uwaga: Trójkąty są przystające jeśli mają odpowiednio równe po dwa boki i po kącie zawartym między tymi bokami.

Zadanie 13
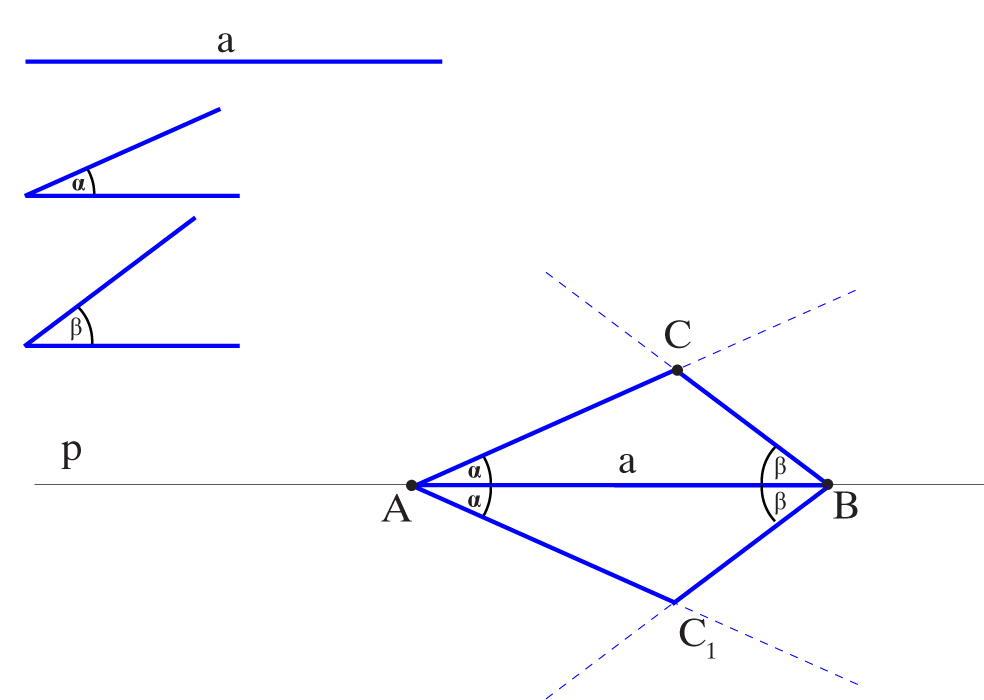
Zbuduj trójkąt mając jego jeden bok a i dwa kąty do niego przyległe α i β.

Opis:
1) Na prostej p odkładam od punktu A odcinek a. Uzyskuję punkt punkt B.

2) Przenoszę kąt α tak, aby jego wierzchołkiem był punkt A a jednym ramieniem prosta p. Powstaje drugie ramię kąta α (nad i pod prostą p).

3) Kąt β przenoszę tak, aby jego wierzchołkiem był punkt B a jednym ramieniem prosta p.

W ten sposób otrzymuję drugie ramię kąta β (nad i pod prostą p), w przecięciu ramion otrzymuję punkty C i C’.

4) Łączę punkt C z punktami A i B (oraz punkt C’ z punktami A i B). Otrzymujemy trójkąt ABC i trójkąt ABC’.

Otrzymane dwa trójkąty są przystające.
Badanie rozwiązalności: Trójkąt da się zbudować, gdy spełniony jest warunek α + β <180°
Uwaga: Trójkąty są przystające jeśli mają odpowiednio równe po jednym boku i po dwa kąty przylegające do tego boku.