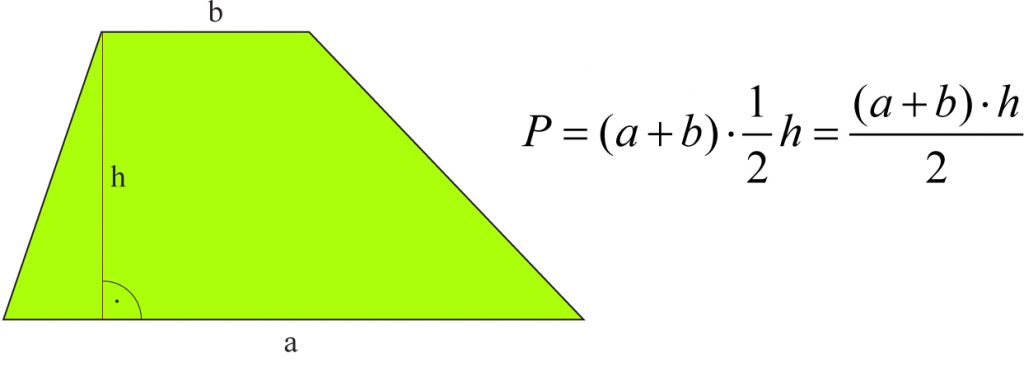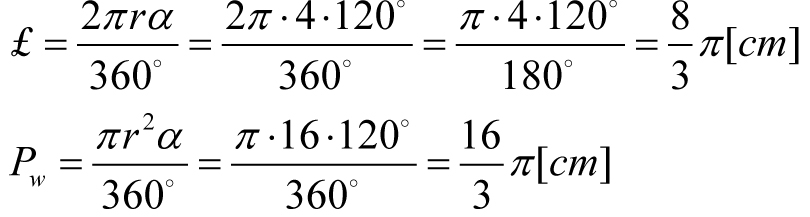Wielokąty
Każdy wielokąt jest częścią płaszczyzny ograniczoną odpowiednią łamaną. Wielkość tej części płaszczyzny można zmierzyć. Do mierzenia używamy „jednostek mierzenia pola powierzchni”, które są kwadratami o odpowiedniej długości boku.
np.:
1 cm² (centymetr kwadratowy), to kwadrat, którego długość boku wynosi 1 cm
1 m² (metr kwadratowy), to kwadrat, którego długość boku wynosi 1 m.
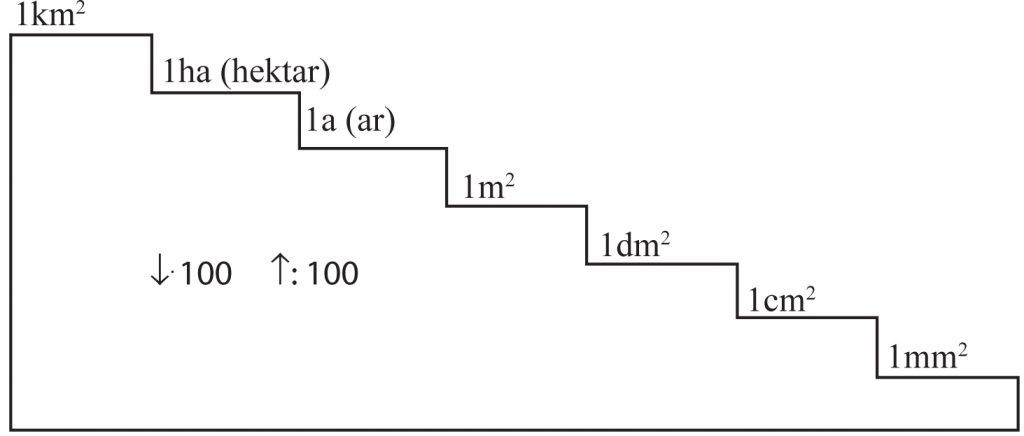
Najczęściej stosuje się poniższe jednostki mierzenia pola powierzchni:
Zamiennikiem jest liczba 100.
Skacząc w dół o 1 stopień – wykonujemy mnożenie przez 100, np.:
1 ha = 100 a 4,5 ha = 450 a
1 a = 100 m² 81,2 a = 8120 m²
1 m² = 100 dm² 0,4 m² = 40 dm² itd.
Skacząc w dół o 2 stopnie – wykonujemy mnożenie przez 100²
Skacząc w dół o 3 stopnie – wykonujemy mnożenie przez 100³ itd.
Idąc w górę o 1 stopień – wykonujemy dzielenie przez 100
Idąc w górę o 2 stopnie – wykonujemy dzielenie przez 100²
Idąc w górę o 3 stopnie – wykonujemy dzielenie przez 100³ np.:
2,5 ha = 2,5 · 100²m²=25000m²
0,45 m² = 0,45 · 100³mm² = 450000 mm²
258,9 cm² = 258,9 : 100²m² = 0,02589 m²
Aby dowiedzieć się, jakie jest pole jakiegokolwiek wielokąta, musimy policzyć, ile razy kwadracik jednostkowy (np.: cm²) mieści się w powierzchni tego wielokąta.
Układanie kwadracików jednostkowych na powierzchni danej figury i policzenie ich jest żmudne i uciążliwe. Ułatwiamy sobie to zadanie wyprowadzając odpowiednie wzory na obliczanie pól figur płaskich.
Prostokąt
Najłatwiej poradzić sobie z prostokątem. Dzielimy go po prostu na jednostki kwadratowe.
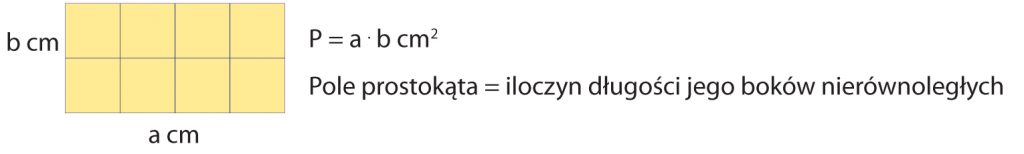
Wzory na pola innych figur wprowadzimy przekształcając je na równoważne im prostokąty.
Zapamiętaj! Figury równoważne, to figury o równych polach powierzchni.
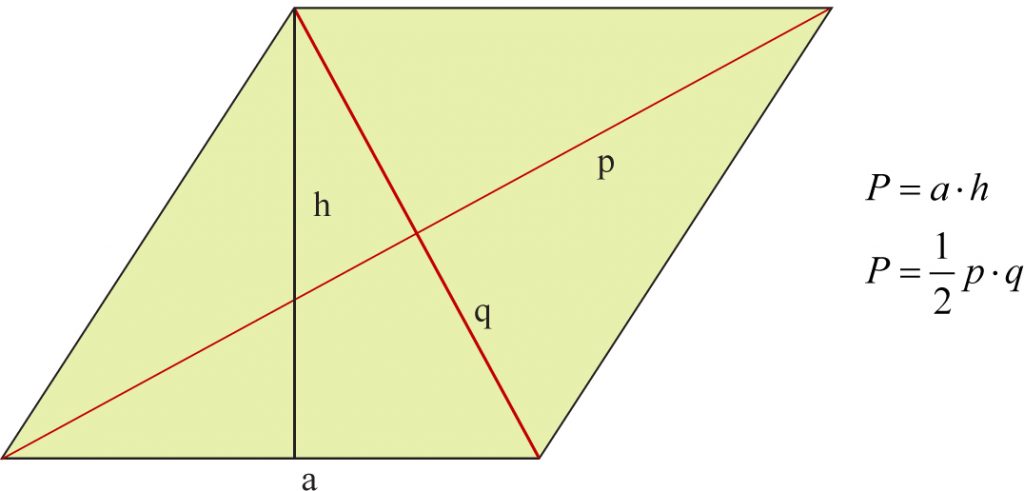
Równoległobok
Pole równoległoboku równe jest iloczynowi długości jego podstawy przez długość wysokości poprowadzonej do tej podstawy.
Romb
Romb jest równoległobokiem, który ma boki równej długości, więc jego pole obliczamy tak jak pole równoległoboku, ale można też inaczej.
Pole rombu równe jest połowie iloczynu długości jego przekątnych.
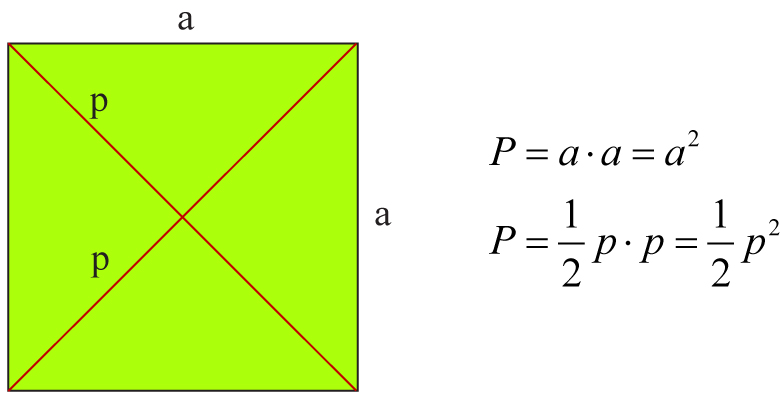
Kwadrat
Kwadrat jest zarówno prostokątem, jak i rombem, więc jego pole obliczamy stosując wzory:
Pole kwadratu równe jest kwadratowi długości jego boku lub połowie kwadratu długości jego przekątnej.
Trójkąt
Pole trójkąta równe jest połowie iloczynu długości jego podstawy przez wysokość poprowadzoną do tej podstawy.
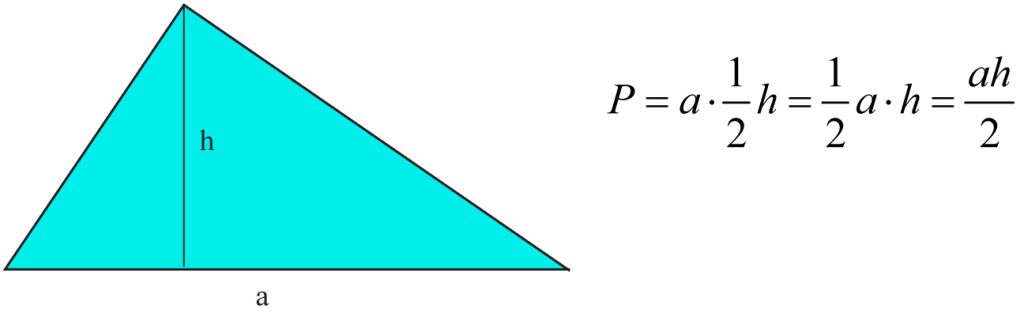
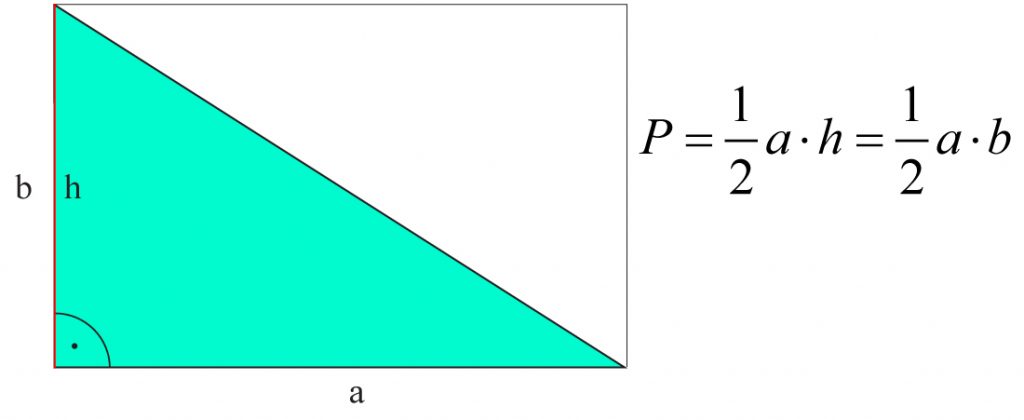
* Trójkąt prostokątny – jest połową prostokąta.
Pole trójkąta prostokątnego równe jest połowie iloczynu długości jego przyprostokątnych.
Trapez
Pole trapezu równe jest połowie iloczynu długości sumy jego podstaw przez długość wysokości.
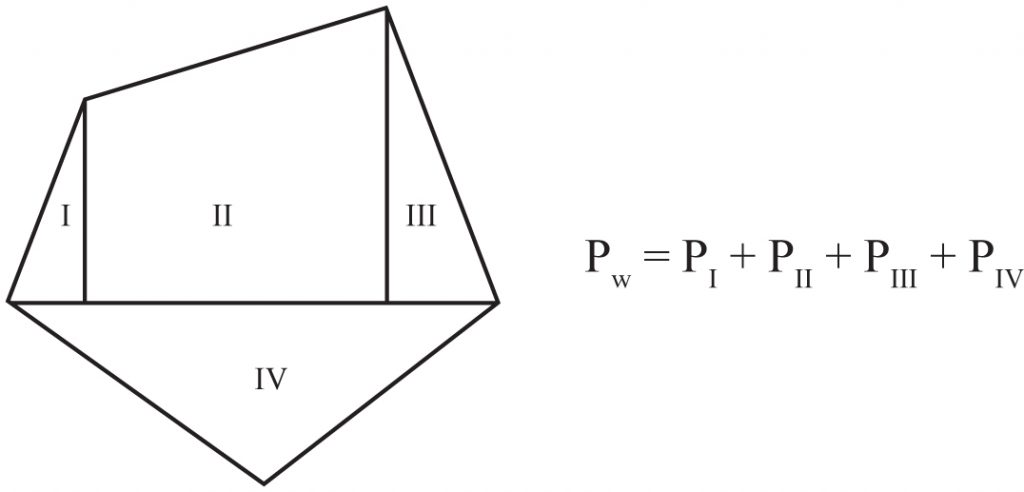
Dowolny wielokąt
Dzielimy go na wielokąty (trójkąty, kwadraty, trapezy…), których pola umiemy obliczyć i sumujemy ich pola.
Zadanie 1
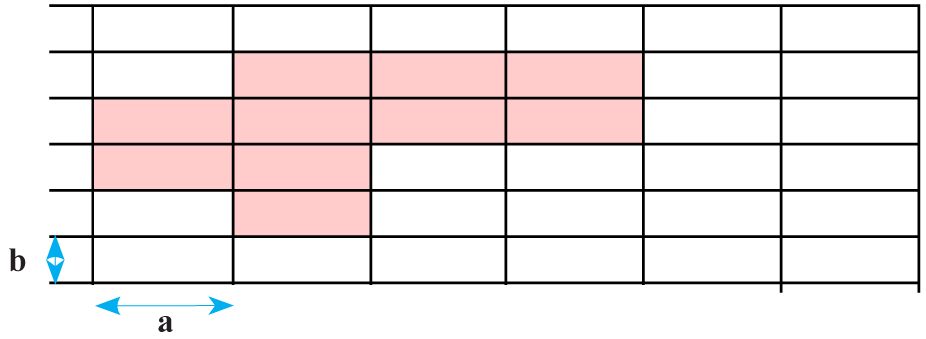
Na rysunku zacieniowano pewną figurę. Oblicz jej pole i obwód.
Pole jednego prostokącika = a . b
Pole figury PF= 10· ab
Obwód figury Obw.F = 8a + 8b = 8(a + b)
Zadanie 2
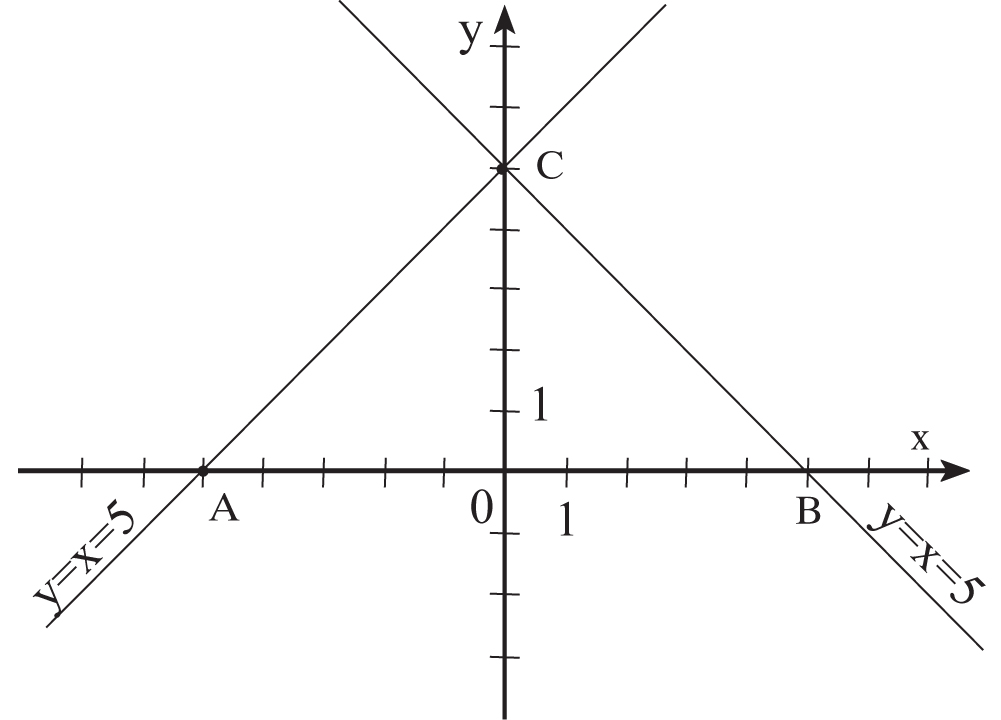
Oblicz pole figury ograniczonej wykresami funkcji y = x + 5;
y = -x + 5 i osią X.
x 0 -5 x 0 5
y=x+5 5 0 y=-x+5 5 0
A = (-5,0)
B = (5,0)
C = (0,5)
|AB| = 10j (jednostek)
|CO| = 5j (jednostek)
Zadanie 3
Oblicz pole figury ograniczonej wykresami funkcji y = 2x – 6; y = 2x – 2 oraz osiami X i Y.
x 0 3 x 0 1
y=2x-6 -6 0 y=2x-2 -2 0
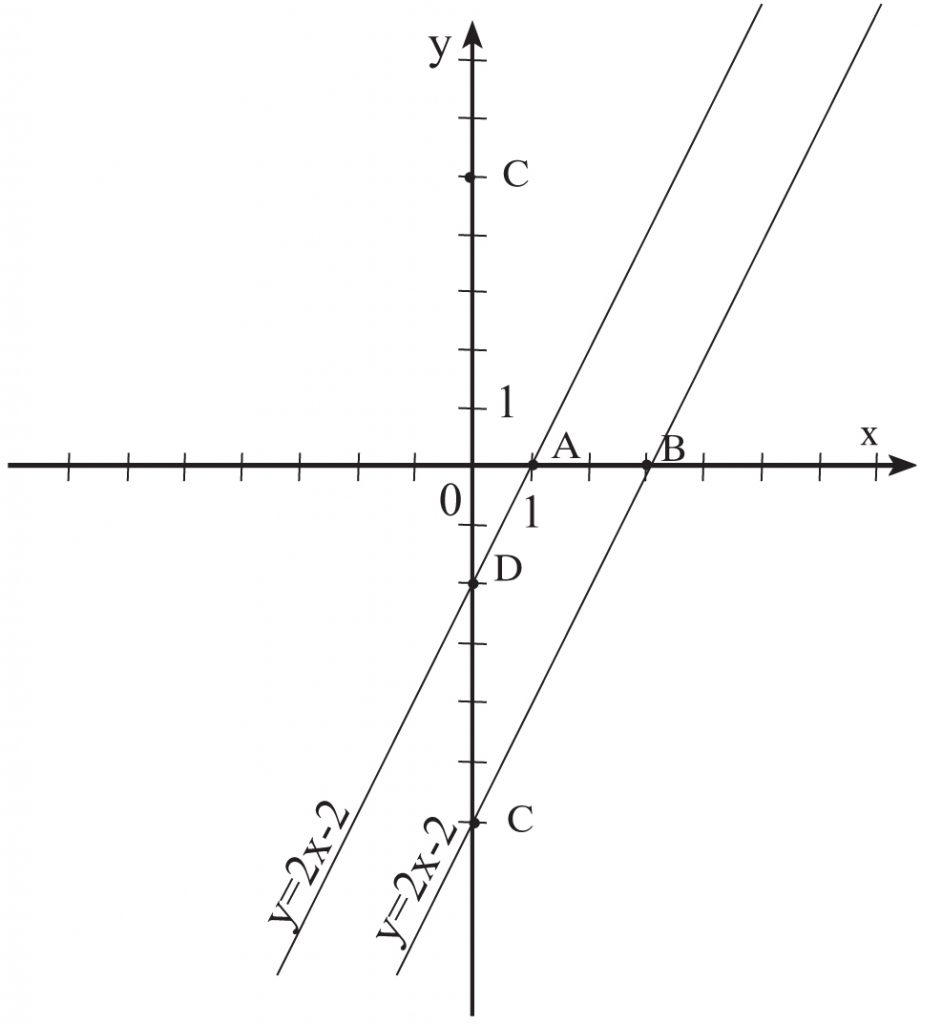
A = (1,0)
B = (3,0)
C = (0,-6)
D = (0,-2)
|OA| = 1 j
|OC| = 6 j
|OB| = 3 j
|OD| = 2 j
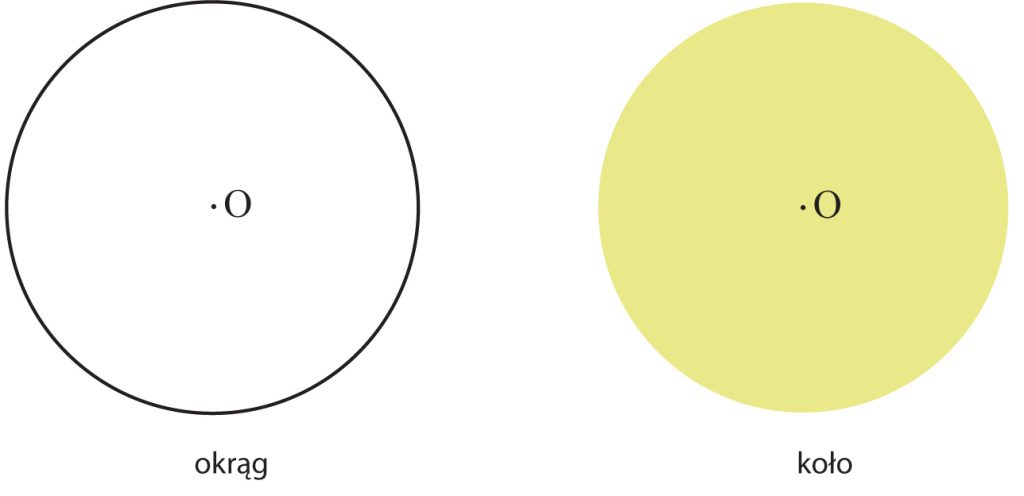
Koło i okrąg
Zbiór punktów płaszczyzny jednakowo oddalonych od stałego punktu tej płaszczyzny (zwanego środkiem) nazywamy OKRĘGIEM.
KOŁO, to część płaszczyzny ograniczona okręgiem, wzięta razem z okręgiem.
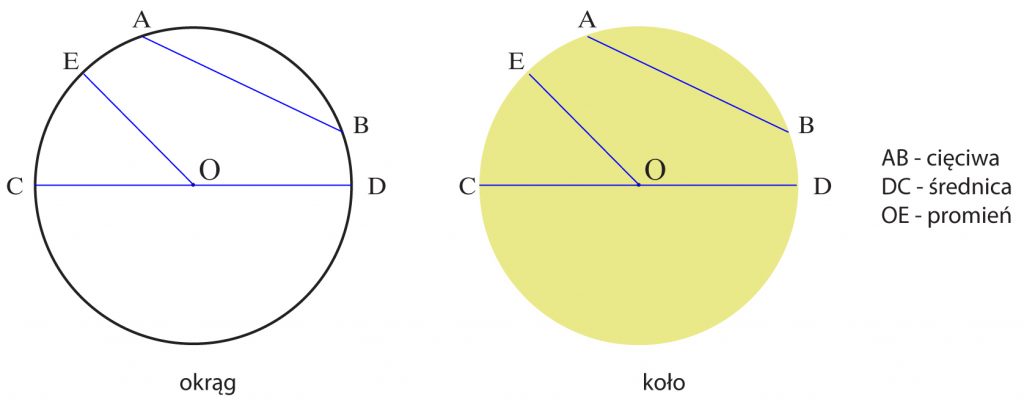
CIĘCIWY OKRĘGU (lub koła) nazywamy odcinek łączący dwa dowolne punkty okręgu.
PROMIENIEM OKRĘGU (lub koła) nazywamy odcinek łączący środek okręgu lub koła z dowolnym punktem okręgu.
ŚREDNICA OKRĘGU (lub koła) to cięciwa przechodząca przez środek okręgu (lub koła).
W każdym kole stosunek długości okręgu tego koła do długości średnicy jest wielkością stałą i równą liczbie niewymiernej π.
π≈3,14
Promień koła oznaczamy symbolem r.
Średnica koła jest dwa razy dłuższa niż promień więc równa jest 2r.
Zatem
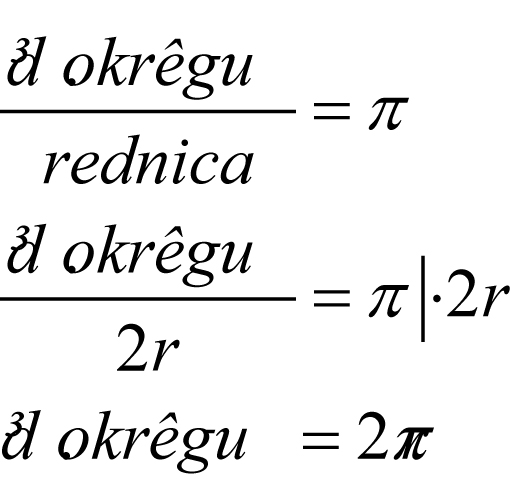
Uwaga: Długość okręgu jest obwodem koła.
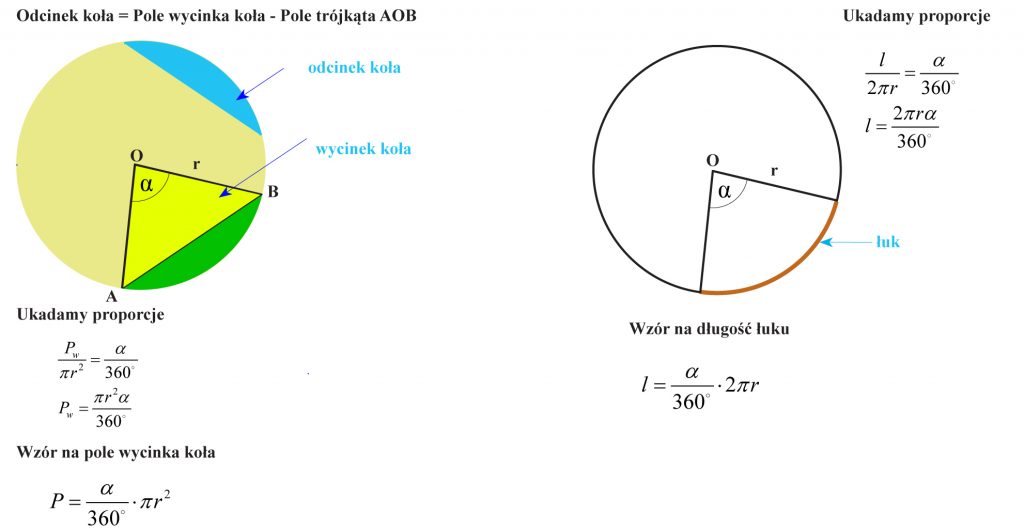
Wzór na pole koła
Zadanie 4
Oblicz długość łuku Ł i pole wycinka kołowego P o kącie α=120° i promieniu r = 4 cm
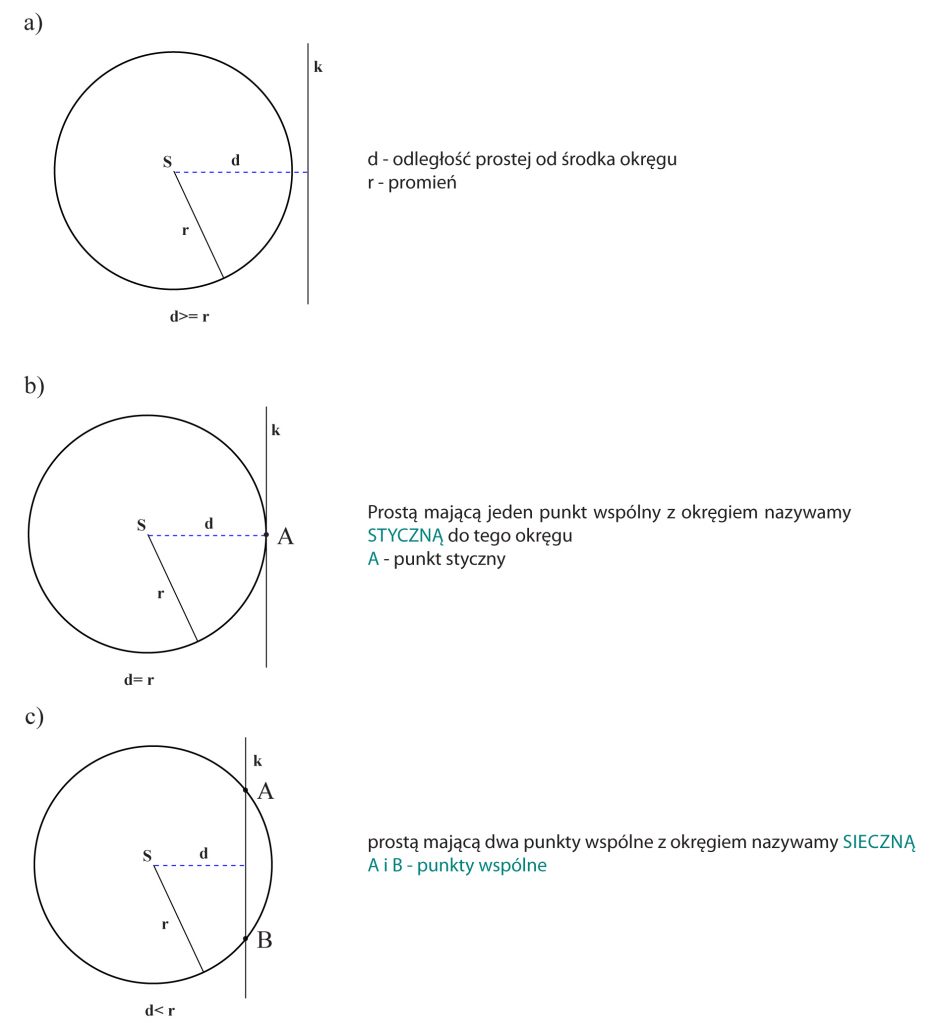
Przypomnijmy sobie, jakie jest wzajemne położenie prostej i okręgu na płaszczyźnie.
Pojęcie WZAJEMNE POŁOŻENIE FIGUR oznacza zazwyczaj ilość punktów wspólnych tych figur.
a zatem:
a) prosta nie ma punków wspólnych z okręgiem
b) prosta ma jeden punkt wspólny z okręgiem
c) prosta ma dwa punkty wspólne z okręgiem
Wzajemne położenie dwóch okręgów na płaszczyźnie
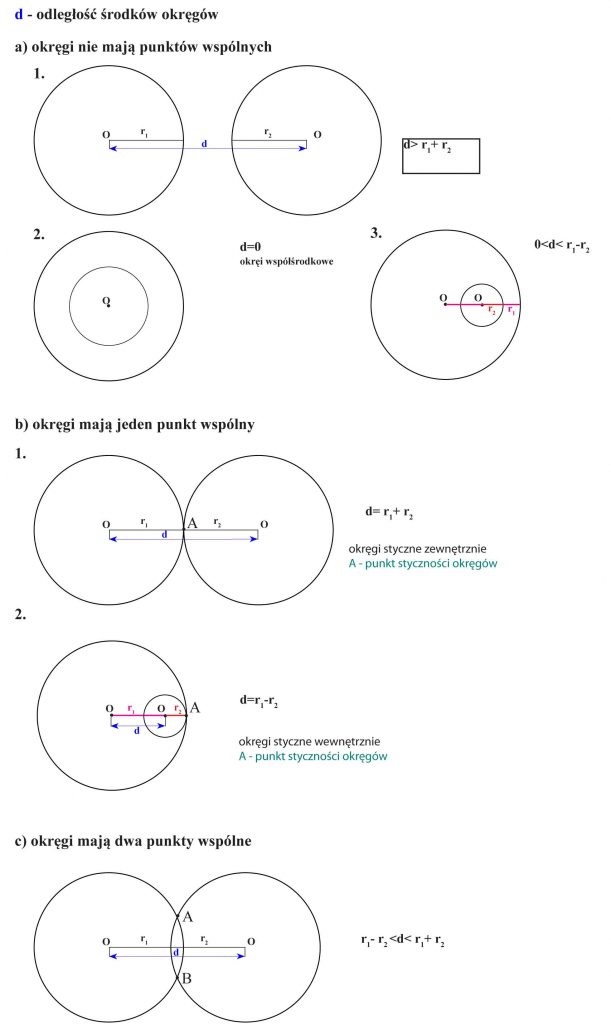
Zadanie 5
Jak położone są względem siebie okręgi, których promienie mają długości 3 cm i 5 cm, a odległość środków okręgów wynosi:
a) 6 cm b) 8 cm c) 2 cm d) 9 cm e) 3 cm f) 1 cm g) 0 cm