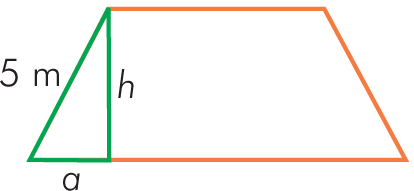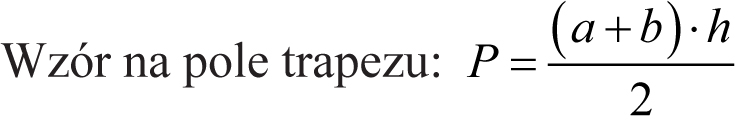Zadanie 1.
Działka jest prostokątem o wymiarach 80 m i 900 dm. Wyraź w arach powierzchnię tej działki.
Rozwiązanie: Ponieważ 1 a = 100 m², więc obliczenia najwygodniej prowadzić w metrach.
Wymiary działki: a = 80 m, b = 900 dm = 90 m. Stąd P = 80 m ⋅ 90 m = 7200 m² = 72 a
Odpowiedź: Powierzchnia działki wynosi 72 ary.
Zadanie 2
Podłoga w przedpokoju ma kształt trapezu. Oblicz koszt położenia płytek w tym przedpokoju, jeżeli firma otrzymała 50 zł za położenie 1m2 płytek.
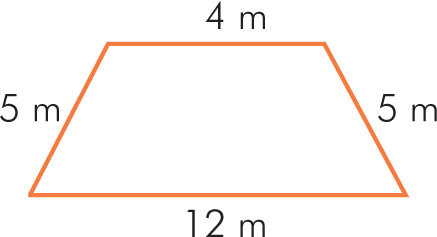
Rozwiązanie: Najpierw z twierdzenia Pitagorasa określamy długość wysokości trapezu:
Odcinek a = ⋅ (12m – 4m) = 4m
4² + h² = 5²
h = 3 [m]
Teraz możemy obliczyć pole powierzchni tej podłogi.
![]()
Koszt położenia to: 24 ⋅ 50 zł = 1200 zł.
Odpowiedź: Koszt położenia płytek wynosi 1200 zł.
Zadanie 3.
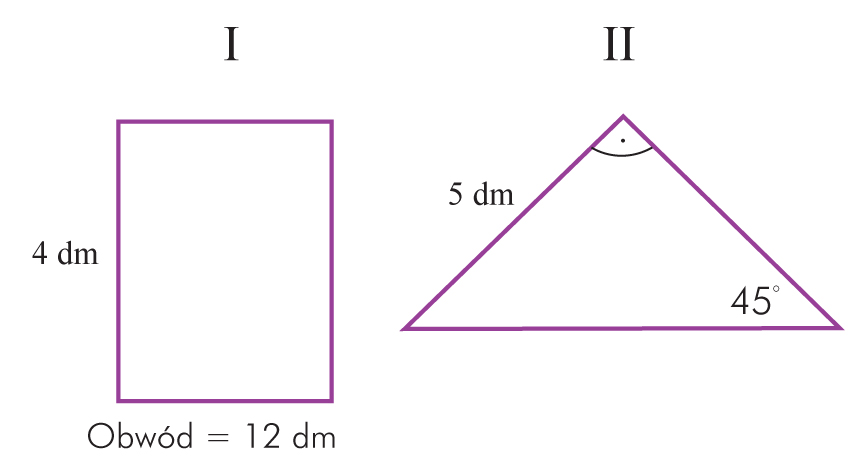
Ala uszyła proporczyk. Wybrała wzór o najmniejszym polu powierzchni. Którą figurę wybrała?
Rozwiązanie: Obliczmy pola obu figur.
I – prostokąt
Skoro obwód wynosi 12 dm, a jeden z boków ma 4 dm, to długość drugiego boku wynosi
⋅ (12 dm – 2 ⋅ 4 dm) = 2 dm.
PI = 2 dm ⋅ 4 dm = 8 dm².
II – trójkąt prostokątny
Przyprostokątne mają długość 5 dm, czyli
PII =![]() = 12,5 dm².
= 12,5 dm².
Odpowiedź: Ala uszyła proporczyk w kształcie prostokąta.
Zadanie 4.
Ile potrzeba koronki na obszycie kwadratowej serwety, której pole wynosi 36 dm²?
Rozwiązanie: Bok serwety wynosi
a² = 36 dm², czyli a = 6 dm
Aby obliczyć ilość potrzebnej koronki, stosujemy wzór na obwód kwadratu L = 4 ⋅ 6 dm = 24 dm.
Odpowiedź: Na obszycie serwety potrzeba 24 dm koronki.
Zadanie 4
Zamień:
a) 48 cm² = ……. mm2
b) 2500 a = ……. ha
c) 2,5 m² = ……. cm2
d) 1,7 km² = ……. a
e) 432,5 m² = ……. ha
f) 58 cm² = ……. dm2
g) 4,7 a = ……. m2
h) 80 ha = ……. a
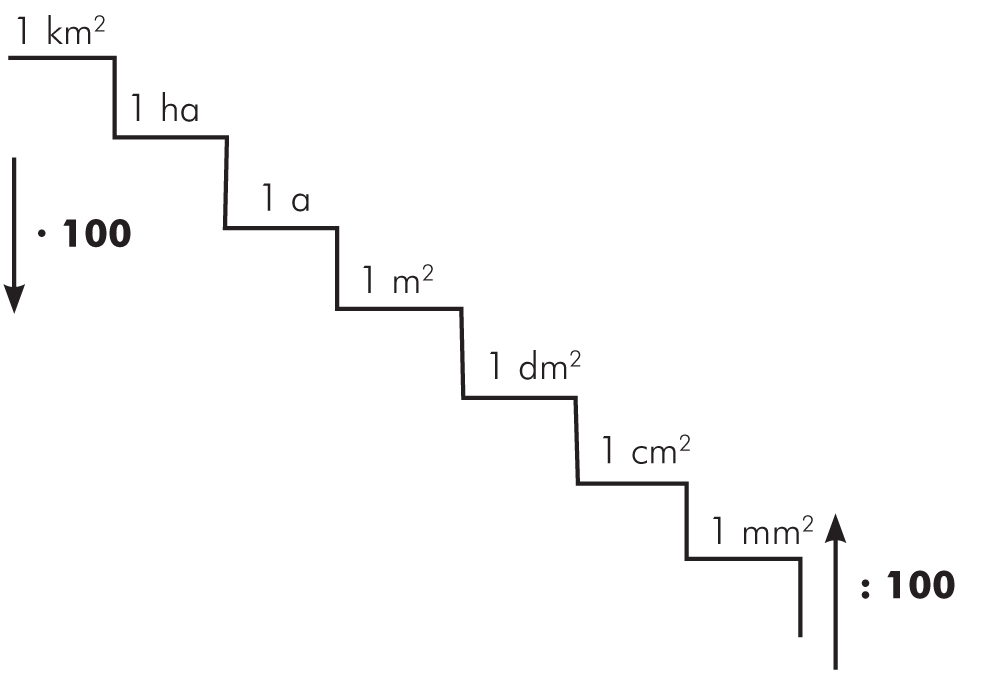
Rozwiązanie: Jeśli nie wiesz, jak zapamiętać zamianę jednostek pola, to może pomogą Ci w tym „schody”!
Jednostki pola
Skacząc w dół o jeden stopień – wykonuj mnożenie przez 100.
Idąc w górę o jeden stopień – wykonuj dzielenie przez 100.
Uwaga! Jeśli np. „skaczesz” w dół o dwa stopnie, to mnożysz przez 10 000 (100 ⋅ 100 = 10 000)
Odpowiedź
a) 48 cm² = 4800 mm²
b) 2500 a = 25 ha
c) 2,5 m² = 25 000 cm²
d) 1,7 km² = 17 000 a
e) 432,5 m² = 0,04325 ha
f) 58 cm² = 0,58 dm²
g) 4,7 a = 470 m²
h) 80 ha = 8000 a
ZAPAMIĘTAJ!
Zadanie na szóstkę!
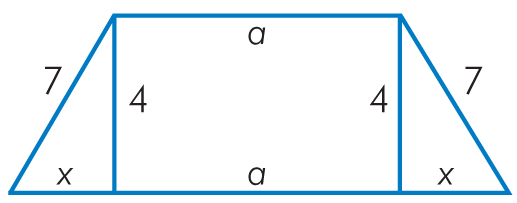
W trapezie równoramiennym ramiona mają długość 7 cm, a wysokość 4 cm. Pole trapezu wynosi 50 cm². Jaki jest obwód tego trapezu?
Rozwiązanie
Wykonajmy rysunek pomocniczy i zapiszmy wzory na pole i obwód trapezu.
![]()
P = = (2a + 2x) · 2
Ponieważ pole wynosi 50 cm2, więc (2a + 2x) ⋅ 2 = 50. Po podzieleniu przez 2 mamy: 2a + 2x = 25.
Teraz napiszmy wzór na obwód:
a + a + x + x + 7 + 7 = 2a + 2x + 14 = (2a + 2x) + 14
Skoro wyrażenie w nawiasie 2a + 2x = 25, to obwód wynosi 25 + 14 = 39 [cm].
Odpowiedź: Obwód trapezu wynosi 39 cm.