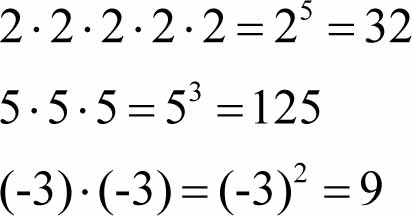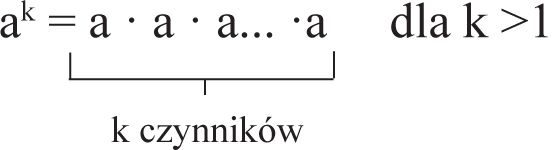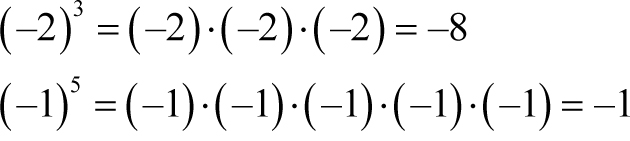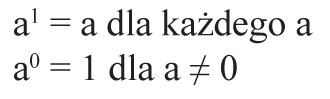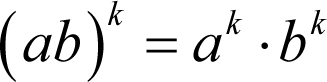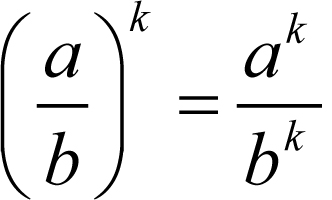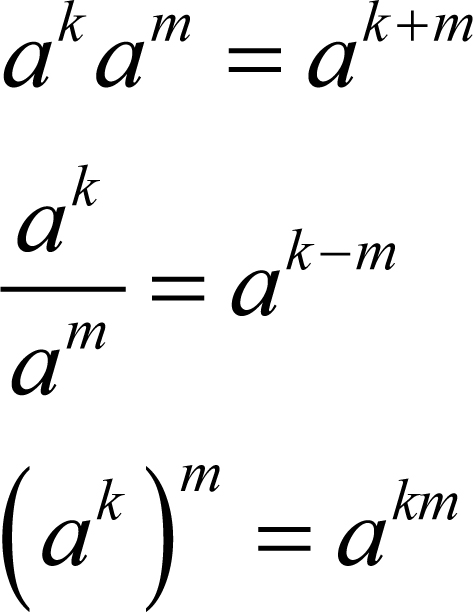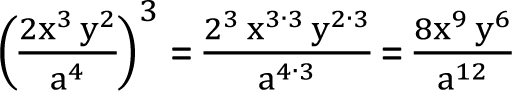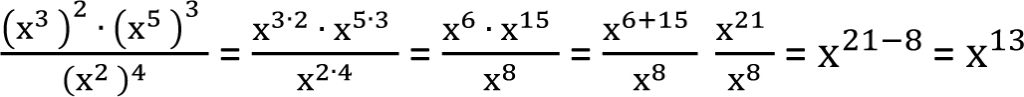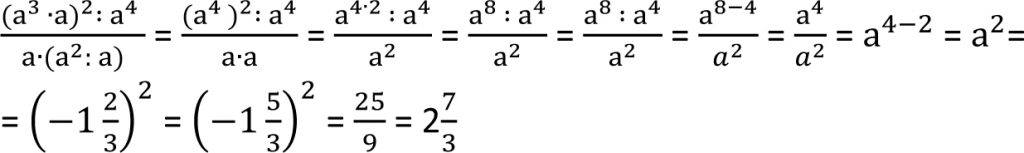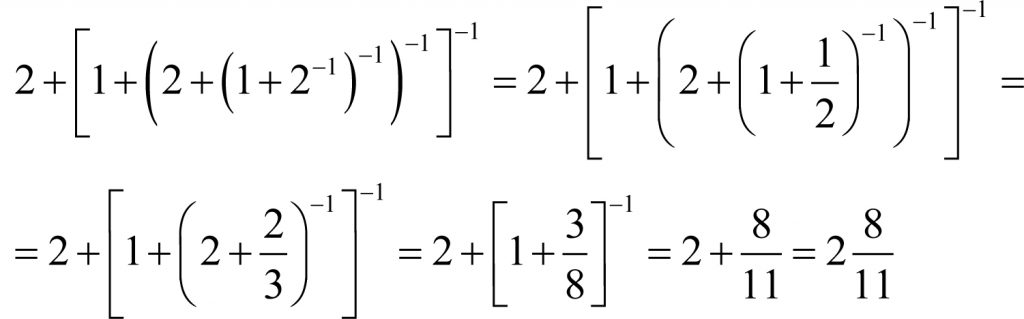Czynność, którą nazywa się potęgowaniem, to nic innego, jak szczególny przypadek znanego nam dobrze mnożenia jednakowych czynników.
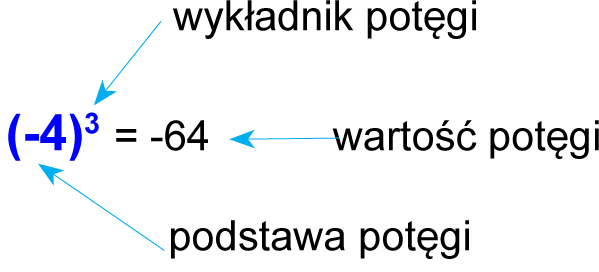
- Podstawa potęgi – informuje nas, jaką liczbę mnożymy przez siebie.
- Wykładnik potęgi – mówi, ile razy podstawę potęgi należy pomnożyć przez siebie.
- Wartość potęgi – to wynik mnożenia.
- Czynność obliczania wartości potęgi nazywamy potęgowaniem.
Powtórzmy sobie wiadomości dotyczące takiego potęgowania, w którym podstawa jest liczbą rzeczywistą natomiast wykładnik należy do zbioru liczb całkowitych.
Definicja potęgi jest trzyczęściowa, a mianowicie:
- I. Potęga o wykładniku naturalnym różnym od zera
Niech a ∈ R \ {0}; k ∈ N , wówczas
Uwaga! a¹ = a
- II. Potęga o wykładniku zerowym
Niech a ∈ R \ {0}; k ∈ N , wówczas
- III. Potęga o wykładniku całkowitym ujemnym
Niech a ∈ R \ {0}; k ∈ N , wówczas
Zapamiętaj!
Podstawa potęgi może być dowolną liczbą rzeczywistą, a więc
- dodatnią
- ujemną
- równą zero
Potęga liczby dodatniej jest liczbą dodatnią, np.:
(0,2)³ = 0,2 . 0,2 . 0,2 = 0,008
1000¹ = 1000
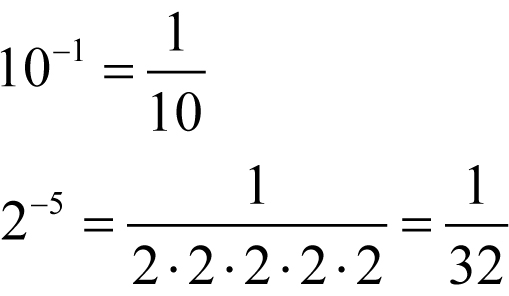
Potęga liczby ujemnej jest liczbą, np.:
- dodatnią, gdy wykładnik potęgi jest liczbą parzystą,
- ujemną, gdy wykładnik potęgi jest liczbą nieparzystą, np.:
Potęga zera jest zerem, np.:
Uwaga!
00 nie oznacza żadnej liczby!
(Nie ma sensu liczbowego!)
Zapamiętaj!
Potęgi możemy mnożyć, dzielić i potęgować
Stosujemy wówczas następujące wzory:
Jeżeli a, b są dowolnymi liczbami rzeczywistymi różnymi od zera;
k, m – dowolnymi liczbami całkowitymi, to:
Przykłady
1. Oblicz
2. Oblicz wartość wyrażenia:
dla a = 
3. Uporządkuj liczby
Czy potęgi można dodawać lub odejmować?
Inny przykład:
Zapamiętaj!
Weźmy pod uwagę potęgę:
