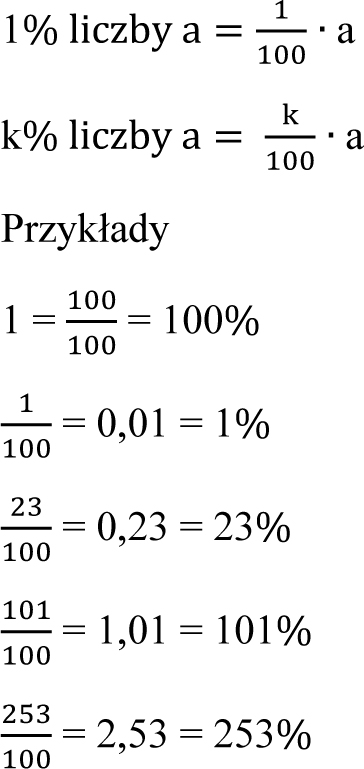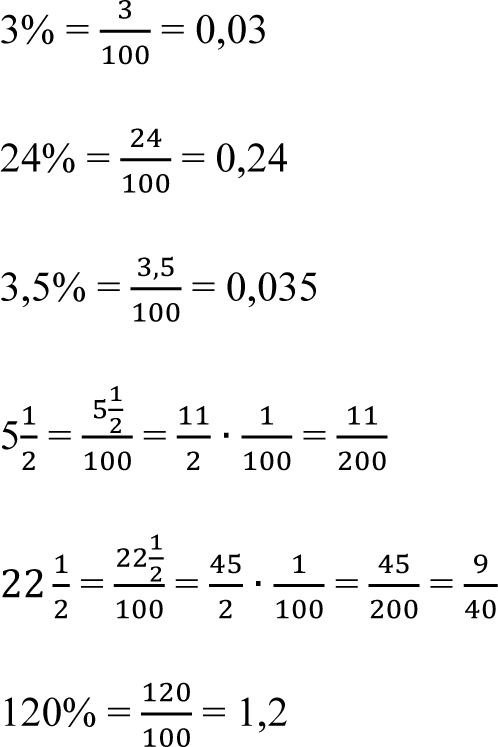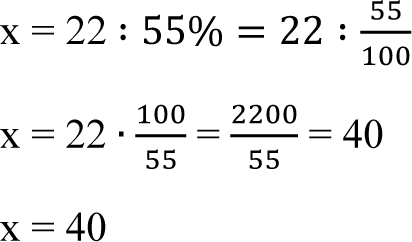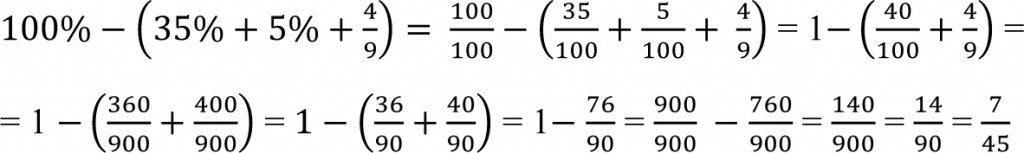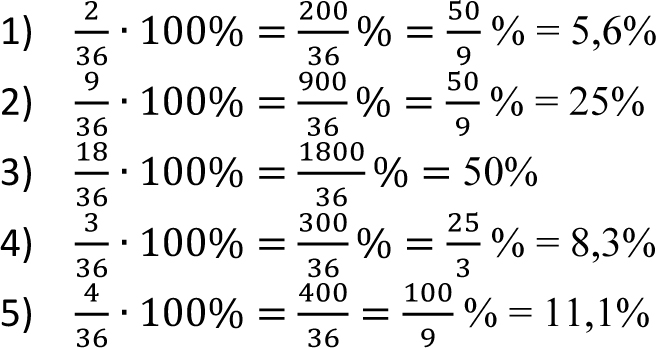Słowo procent oznacza setną część danej wielkości. Słowo to pochodzi z języka łacińskiego i znaczy „od stu” lub „za sto”. Procent oznaczamy następującym znakiem: %.
Ułamki zamieniamy na procenty wykonując mnożenie przez 100, np.:
Procenty zamieniamy na ułamki wykonując dzielenie przez 100, np.:
Zadanie 1
Jajko zawiera 58% białka, 32% żółtka, a reszta to skorupka. Oblicz, jaką częścią jajka jest skorupka?
Rozwiązanie:
Jajko stanowi 100%, a więc skorupka stanowi:
100% – (58% + 32%) = 100% – 90% = 10% jajka.
A jaka to część jaja? Zamieniamy 10% na ułamek, czyli:
Odp.: Skorupka stanowi 0,1 część jajka.
Zadanie 2
Co to znaczy, że 100% uczniów klasy II otrzymało promocję do klasy następnej?
Odp.: To znaczy, że wszyscy uczniowie otrzymali promocję.
Występują trzy główne typy zadań z zastosowaniem procentów
- Obliczanie procentu danej liczby.
- Obliczanie liczby z danego jej procentu.
- Obliczanie jakim procentem jednej liczby jest druga.
I. Obliczanie procentu danej liczby
Zadanie:
Klasa VI liczy 40 uczniów. 55% wszystkich uczniów stanowią dziewczęta. Ile jest dziewcząt?
Dane:
- liczba wszystkich uczniów – 40
- procent jaki stanowią dziewczęta – 55%
Szukana
- liczba dziewcząt (czyli wartość tego procentu).
Rozwiązanie:
Odp.: Klasa VI liczy 22 dziewczęta.
Zapamiętaj!
Aby obliczyć procent danej liczby, należy zamienić go najpierw na ułamek, a potem pomnożyć ten ułamek przez daną liczbę.
II. Obliczanie wielkości z danego jej procentu
Zadanie
W klasie VI są 22 dziewczęta, co stanowi 55% wszystkich uczniów. Ilu uczniów jest w klasie VI?
Dane:
- ilość dziewcząt – 22 (wartość procentu)
- procent, który stanowią dziewczęta – 55%
Szukana – liczba uczniów klasy VI.
Rozwiązanie:
Odp.: Klasa VI liczy 40 uczniów.
Można to zadanie rozwiązać inaczej, przy pomocy równania.
Przez x oznaczmy szukaną liczbę uczniów klasy VI, wtedy 55% · x = 22
Odp.: Klasa VI liczy 40 uczniów.
Zapamiętaj!
Aby obliczyć liczbę z danego jej procentu należy wartość procentu podzielić przez ten procent zamieniony na ułamek.
III. Obliczanie jakim procentem jednej liczby jest druga
Zadanie
W klasie VI jest 40 uczniów, w tym 22 dziewczynki. Jaki procent wszystkich uczniów stanowią dziewczęta?
Dane:
- ilość wszystkich uczniów – 40
- Ilość dziewcząt – 22 (wartość procentu)
Szukane
- jaki to procent?
Rozwiązanie:
Odp.: Dziewczęta stanowią 55% wszystkich uczniów.
Zapamiętaj!
Aby obliczyć jakim procentem jednej liczby jest druga należy wykonać dzielenie jednej liczby przez drugą i ten ułamek zamienić na procent mnożąc go przez 100.
Zadanie
Cena 1 kg pewnego towaru wynosiła 16 zł. Towar ten podrożał o 7,5%. Jaka jest nowa cena?
Rozwiązanie:
1) Obliczam o ile zł podrożał towar. 7,5% z 16 =![]() zł
zł
2) Jaka jest nowa cena? 16 + 1,2 = 17,2 zł
Zadanie
Przy przemiale zboża rozkurz stanowi 3%, a otręby 15% ciężaru zboża. Reszta to mąka. Ile zboża trzeba zemleć aby otrzymać 2,4 tony mąki.
Rozwiązanie:
1) Obliczam jaki procent ziarna stanowi mąka
100% – (3% + 15%) = 100% – 18% = 82%
2) Wiedząc, że 82% stanowi 2,4t obliczam ilość zboża
Odp.: Należy zemleć 2,9 t zboża.
Zadanie 3
Obszar dorzecza Wisły wynosi 168 646 km², a powierzchnia Polski liczy 312 677 km². Jaki procent powierzchni Polski stanowi dorzecze Wisły?
Rozwiązanie:
Odp.: Dorzecze Wisły stanowi 53,9% obszaru Polski.
Zadanie
Budynek gospodarczy zajmuje 5% powierzchni placu szkolnego, ogród – 35%, boisko – 5/9. Pozostałe 840 m2 zajmuje budynek szkolny. Jaka jest powierzchnia całego placu?
Rozwiązanie:
1) Obliczam jaki ułamek całego placu zajmuje budynek szkolny
2) Obliczam powierzchnię całego placu
Odp. Plac szkolny ma 5400 m² powierzchni.
Diagramy procentowe
Bardzo ważną umiejętnością związaną z procentami jest budowanie diagramów procentowych. Mogą to być diagramy kwadratowe, prostokątne lub kołowe – w zależności od kształtu rysowanej figury.
Powtórzmy kreślenie diagramów w oparciu o następujące zadanie:
W pewnej klasie VI, liczącej 36 osób, uzyskano następujące oceny z matematyki w klasyfikacji półrocznej:
- 2 oceny – bdb,
- 9 ocen – db,
- 18 ocen – dst
- 3 oceny – mrn
- 4 oceny – ndst.
Nakreśl diagram procentowy wyników tej klasyfikacji.
Rozwiązanie:
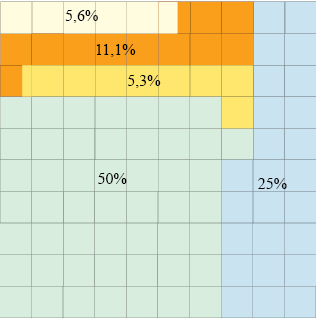
I. Diagram kwadratowy
Kreślimy kwadrat o boku 10 jednostek, którego pole równe jest 100 jednostek kwadratowych (j2). 1 j2 oznacza 1%.
Policzmy, jaki procent stanowią poszczególne oceny:
(sprawdzamy: 5,6% + 25 % + 50% + 8,3% + 11,1% = 100% – czyli nie ma pomyłki w obliczeniach).
- Oceny bdb zajmują zatem 5,6 kratki w diagramie
- Oceny db zajmują zatem 25 kratek w diagramie
- Oceny dst zajmują zatem 50 kratek w diagramie
- Oceny mrn zajmują zatem 8,3 kratki w diagramie
- Oceny ndst zajmują zatem 11,1 kratki w diagramie.
II. Diagram prostokątny
Kreślimy prostokąt, którego pole wynosi 100 j2. Jego wymiary to najczęściej:
20 j x 5 j lub 25 j x 4 j.
Obliczenia przenoszę z poprzedniego diagramu:
- 5,6% czyli 5,6 kratki – oceny bdb
- 25% czyli 25 kratek – oceny db
- 50% czyli 50 kratek – oceny dst
- 8,3% czyli 8,3 kratki – oceny mrn
- 11,1% czyli 11,1 kratki – oceny ndst.
III. Diagram kołowy
W diagramie kołowym występuje dodatkowa trudność polegająca na wyliczeniu wielkości kątów środkowych odpowiadających poszczególnym obliczeniom procentowym.
Całemu kołu – czyli kątowi pełnemu (360°) odpowiada 100%.
Jednemu procentowi odpowiada kąt środkowy o mierze ![]()
Zadanie
Posługując się podaną tabelką sporządzić diagramy: kwadratowy, prostokątny i kołowy przedstawiający procentowy podział powierzchni lądów naszego globu na części Ziemi.
Części świata Pole powierzchni w milionach km2
Europa 10,3
Azja 44,3
Afryka 30,3
Ameryka 42,1
Australia I Oceania 8,6
Antarktyda 14,1
1) Obliczam pole powierzchni wszystkich lądów:
10,3 + 44,3 + 30,3 + 42,1 + 8,6 + 14,1 = 149,7
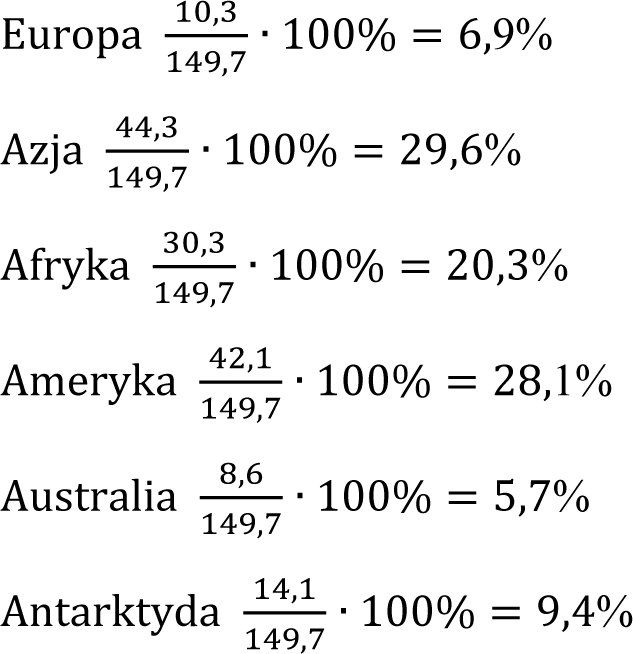
2) Obliczam, jaki procent stanowi każdy ląd w porównaniu do całości
3) Obliczam wielkości kątów środkowych odpowiadające poszczególnym procentom:
Europa 6,9 · 3,6° = 24,8°
Azja 29,6 · 3,6° = 106,6°
Afryka 20,3 · 3,6° = 73°
Ameryka 28,1 · 3,6° = 101,2°
Australia 5,7 · 3,6° = 20,5°
Antarktyda 9,4 · 3,6° = 33,9°
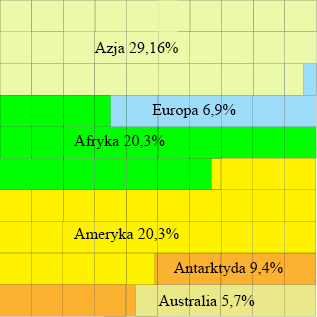
4) Korzystam z powyższych obliczeń i kreślę diagramy
kwadratowy
prostokątny
kołowy
Uwaga! Procenty mają szerokie zastosowanie w życiu codziennym np. w bankowości. Łatwo można obliczyć, który bank oferuje korzystniejsze warunki i tam ulokować swoje oszczędności.