Prostopadłościan
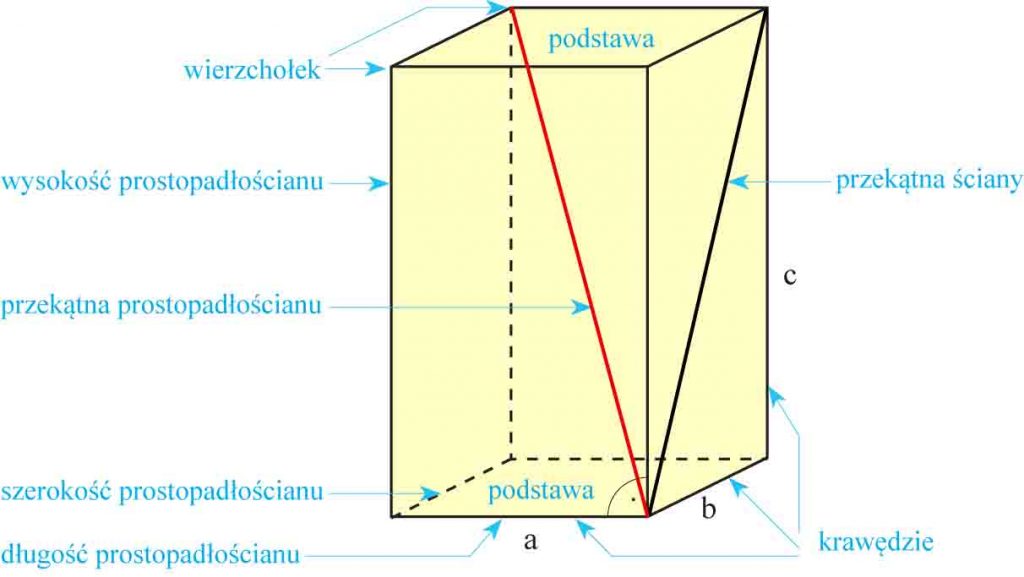
- Prostopadłościan jest to graniastosłup prosty, którego wszystkie ściany są prostokątami.
- Każda ściana prostopadłościanu może być podstawą albo ścianą boczną; zależy od jego ustawienia.
- Długości krawędzi podstawy nazywamy odpowiednio długością i szerokością prostopadłościanu, a długość krawędzi bocznej wysokością prostopadłościanu.
- Przekątną ściany nazywamy przekątną prostokąta będącego ścianą prostopadłościanu.
- Przekątną prostopadłościanu nazywamy odcinek łączący dwa wierzchołki prostopadłościanu nienależące do jednej ściany.
- Prostopadłościan ma 6 ścian, w tym 2 podstawy i 4 ściany boczne, a także 12 krawędzi, 8 wierzchołków i 4 przekątne.
- Pole powierzchni prostopadłościanu jest równe sumie pól wszystkich jego ścian: P = 2ab + 2ac +2bc
- Objętość prostopadłościanu jest iloczynem wszystkich krawędzi wychodzących z jednego wierzchołka: V = abc
Uwaga!
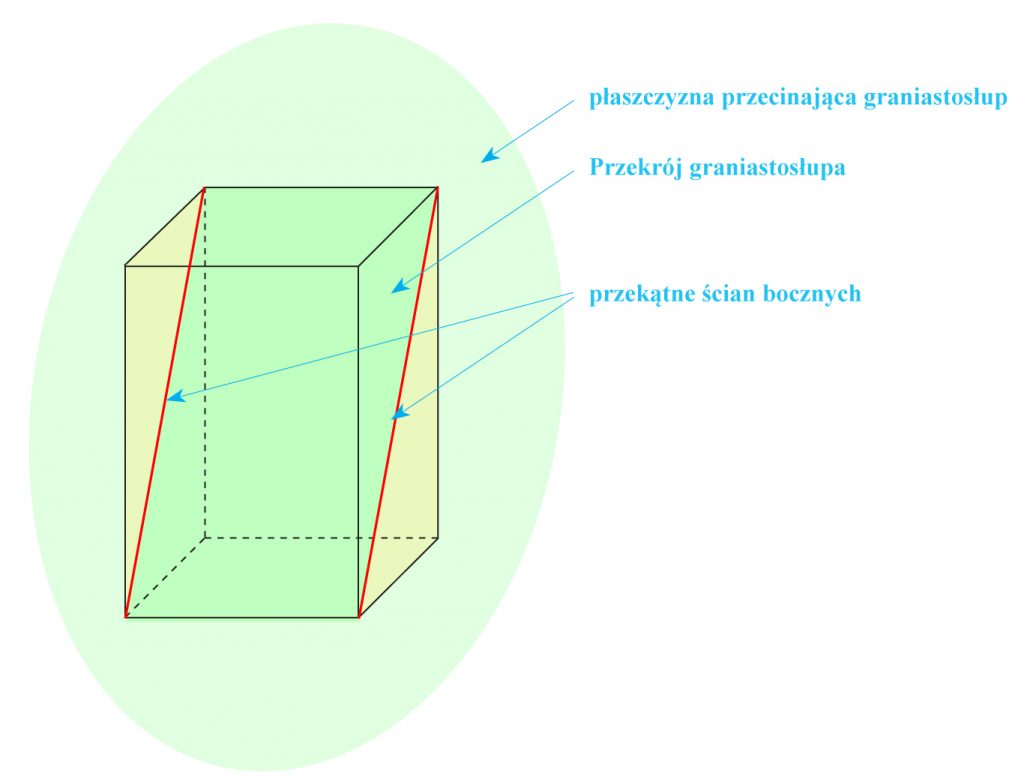
Przekrojem graniastosłupa nazywamy część wspólną graniastosłupa i płaszczyzny przecinającej ten graniastosłup.
Zobacz na przykładzie:
przekrój prostopadłościanu płaszczyzną przechodzącą przez przekątne dwóch przeciwległych ścian
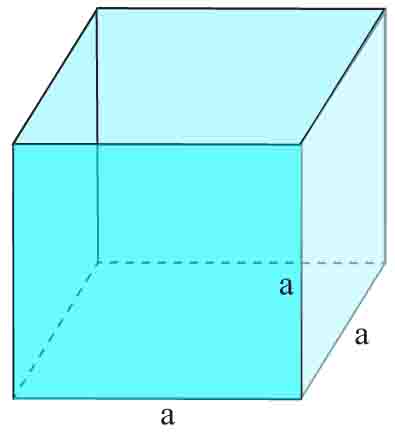
Sześcian
a – długość krawędzi sześcianu
- Sześcian to prostopadłościan, którego każda ściana jest kwadratem.
- W sześcianie wszystkie krawędzie są równej długości.
- Pole powierzchni sześcianu jest równe sumie pól sześciu kwadratów: P = 6a²
- Objętość sześcianu jest równa iloczynowi trzech krawędzi wychodzących z jednego wierzchołka: V = a³.
- Każde dwa sześciany są podobne (są figurami podobnymi).
To ważne!
Jeśli dwie figury przestrzenne są podobne w skali k, to:
- stosunek ich pól powierzchni wynosi k²
- stosunek ich objętości wynosi k³.
Ważna wiedza w pigułce
Jednostki objętości
1 cm³ = 10³ mm³
1 dm³ = 10³ cm³
1 m³ = 10³ dm³
1 l = 1 dm³
1 ml = 10-³ l
1 l = 10³ ml
1 hl = 100 l
Zadanie 1.
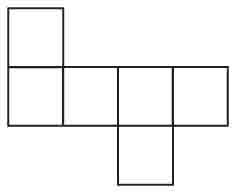
Rysunek przedstawia siatkę sześcianu o krawędzi 10.
a) Oblicz sumę długości wszystkich jego krawędzi.
b) Oblicz pole powierzchni tego sześcianu.
c) Oblicz objętość tego sześcianu.
Rozwiązanie
a) W każdym sześcianie jest 12 krawędzi równej długości, czyli ich suma wynosi 12 · 10 = 120 [j].
b) P = 6 · 10² = 600 [j²]
c) V = 10³ = 1000 [j³]
Zadanie 2.
Na wykonanie szkieletu prostopadłościanu o krawędziach podstawy długości 10 cm i 6 cm zużyto 124 cm drutu. Jaka jest wysokość tego prostopadłościanu?
Rozwiązanie
Oznaczmy przez h długość szukanej wysokości. Prawdziwe jest zatem równanie:
4 · 10 cm + 4 · 6 cm + 4 · h = 124 cm
64 cm + 4 h = 124 cm
h = 15 cm
Odpowiedź: Wysokość prostopadłościanu wynosi 15 cm.
Zadanie 3.
Ile decymetrów kwadratowych papieru zużyto na oklejenie sześciennego pudełka (sześcianu), którego objętość wynosi 0,125 m³?
Rozwiązanie:
Dokonamy najpierw zamiany jednostek: 0,125 m³ = 125 dm³.
Ze wzoru na objętość sześcianu wynika, że długość krawędzi
Korzystając teraz ze wzoru na pole powierzchni sześcianu, mamy, że P = 6 · 5² = 150 [dm²].
Odpowiedź: Na oklejenie pudełka zużyto 150 dm² papieru.
Zadanie 4.
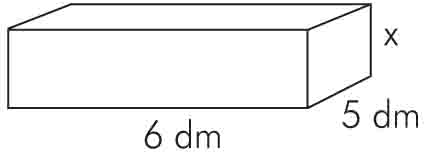
Akwarium w kształcie prostopadłościanu o długości 0,6 m, szerokości 50 cm i wysokości 4 dm napełniono do połowy wodą. O ile centymetrów podniesie się poziom wody w akwarium, jeżeli wlejemy do niego 8 butelek wody o pojemności 750 ml?
Rozwiązanie: Ponieważ 750 ml = 3/4 l, to objętość wody wlanej do akwarium z 8 butelek wynosi
8 · 3/4 l = 6 l = 6 dm³.
Jednocześnie można stwierdzić, że objętość wlanej wody jest równa objętości prostopadłościanu o długości 6 dm, szerokości 5 dm i wysokości x.
Zatem 6 dm · 5 dm · x = 6 dm³, czyli x = 0,2 dm = 2 cm.
Uwaga! Do rozwiązania zadania tym sposobem nie była nam potrzebna wysokość akwarium ani informacja o tym, że jest ono napełnione wodą do połowy.
Odpowiedź: Poziom wody w akwarium podniesie się o 2 cm.
Zadanie 5
Akwarium wypełnione do połowy wodą waży 19 kg, a wypełnione całkowicie wodą 34 kg. Ile waży puste akwarium?
Rozwiązanie:
Niech x oznacza wagę wody wypełniającej całkowicie akwarium, a y wagę pustego akwarium. Mamy wtedy:
0,5x + y = 19
x + y = 34
Po wymnożeniu pierwszego równania przez –1, a potem dodaniu równań stronami otrzymujemy, że 0,5x = 15, czyli x = 30 [kg]. Skoro waga wody wynosi 30 kg, to waga pustego akwarium jest równa 4 kg.
Odpowiedź:
Puste akwarium waży 4 kg.
Zadanie 6
Czy w kartonie o wymiarach zewnętrznych 6,3 cm x 9,5 cm x 17 cm zmieści się 1 litr mleka? Przyjmij, że grubość ścianki wynosi 0,5 mm.
Rozwiązanie:
Określmy wymiary wewnętrzne kartonu, pamiętając, że od wymiarów zewnętrznych musimy odjąć 0,1 cm (2 · 0,5 mm = 1 mm).
Wynoszą one: 6,2 cm; 9,4 cm; 16,9 cm. Wyliczymy objętość prostopadłościanu o tych wymiarach
V = 6,2 cm · 9,4 cm · 16,9 cm ≈ 985 cm³ ≈ 0,985 dm³
Wniosek: 0,985 dm3 < 1litra.
Odpowiedź: Jeden litr mleka nie zmieści się w kartonie o podanych wymiarach.
Zadanie 7
Skrzynka na kwiaty jest prostopadłościanem, którego podstawa ma wymiary 24 cm i 90 cm. Wysokość skrzynki stanowi 20% dłuższej krawędzi podstawy. Ile 5-litrowych worków ziemi trzeba kupić, aby ją całkowicie napełnić? Zapisz wszystkie obliczenia.
Rozwiązanie: Objętość skrzynki wynosi
V = 24 cm · 90 cm · 0,2 · 90 cm = 38 880 cm³ = 38,88 dm³ = 38,88 l.
Teraz obliczamy liczbę worków ziemi, którą trzeba zakupić 38,88 : 5 = 7,776 ≈ 8
Odpowiedź: Aby całkowicie napełnić skrzynkę, trzeba kupić 8 worków ziemi.
Zadanie domowe!
1) Pole powierzchni prostopadłościanu o krawędziach długości 1,2 dm, 5 cm, 0,1 m wynosi:
A. 2,3 dm²
B. 4,6 dm²
C. 0,6 dm2
D. 13,24 dm²
2) Z akwarium o wymiarach podstawy 5 dm x 4 dm i wysokości 3,6 dm napełnionego do połowy wodą odlano 4 litry wody. O ile centymetrów obniżył się poziom wody w akwarium?
A. 1,8 cm
B. 2 cm
C. 11 cm
D. 20 cm
3) Ściany boczne 6 kolumn w kształcie prostopadłościanu o wymiarach podstawy 3 dm x 3 dm i wysokości 3,5 m pomalowano farbą. Ile litrów farby zużyto, jeśli dwulitrowa puszka farby starcza na pomalowanie 14 m² powierzchni?
A. 0,9 l
B. 1,8 l
C. 3,6 l
D. 7,2 l
Rozwiązanie
1) B
Wymiary przedstawimy w decymetrach, bo podane odpowiedzi są zapisane w decymetrach kwadratowych. Wynoszą one 1,2 dm, 0,5 dm i 1 dm. Liczymy pole powierzchni:
P = 2 · 1,2 dm · 0,5 dm + 2 · 1,2 dm · 1 dm + 2 · 1 dm · 0,5 dm = 1,2 dm² + 2,4 dm² + 1 dm² = 4,6 dm².
2) B
x – długość szukanego odcinka
5 dm · 4 dm · x = 4 dm³
x = 0,2 dm = 2 cm
3) C
Skoro mamy 6 kolumn, a każda ma 4 ściany boczne, to razem mamy do pomalowania 24 prostokąty o wymiarach 0,3 m
i 3,5 m. Pole wynosi: P = 24 · 0,3 m · 3,5 m = 25,2 m². Skoro 2 litry farby wystarczają na pomalowanie 14 m² powierzchni, to jednym litrem pomalujemy 7 m² powierzchni. Z tego wynika, że na pomalowanie 25,2 m² powierzchni potrzeba 3,6 litra farby (25,2 : 7 = 3,6).
Poćwicz 2
1. Na rysunku niżej przedstawiono siatkę graniastosłupa prawidłowego trójkątnego. Ile wynosi suma długości wszystkich krawędzi tego graniastosłupa?
A. 50
B. 38
C. 33
D. 29
2. Szałas pasterski wykonano z drewna sosnowego, którego gęstość jest równa 0,47 g/cm3. Na budowę tego szałasu zużyto 3,5 m3 sosnowych desek o jednakowych wymiarach: 10 cm, 20 cm, 350 cm. Jaką objętość ma jedna deska sosnowa?
A. 700 cm³
B. 1400 cm³
C. 14 000 cm³
D. 70 000 cm³
3. Ile cegieł o wymiarach 25 x 12 x 6 cm potrzeba, aby wybudować murowane ogrodzenie o długości 4,5 m, wysokości 2 m i grubości 0,25 m, wiedząc, że 20% objętości muru stanowi zaprawa murarska. Zapisz obliczenia.
Odpowiedzi:
1. C.
2. D.
3. Objętość jednej cegły:
Vcegły = 25 · 12 · 6= 1800 [cm³]
Murowane ogrodzenie ma kształt prostopadłościanu, którego objętość wynosi:
Vmuru = 4,5 · 2 · 0,25 = 2,25 [m³] = 2 250 000 [cm³]. Ponieważ 20% objętości muru stanowi zaprawa murarska, zatem zużyte cegły stanowią 80% objętości muru, czyli 1 800 000 cm³
(0,8 · 2 250 000 = 1 800 000). Liczbę zużytych cegieł do wybudowania muru otrzymamy po wykonaniu działania 1 800 000 : 1800 = 1000.
Odpowiedź:
Do wybudowania ogrodzenia potrzeba zatem 1000 cegieł.