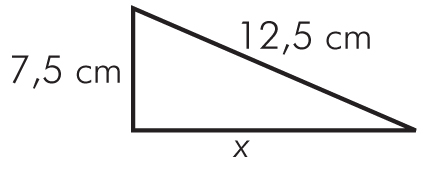Wiedza w pigułce
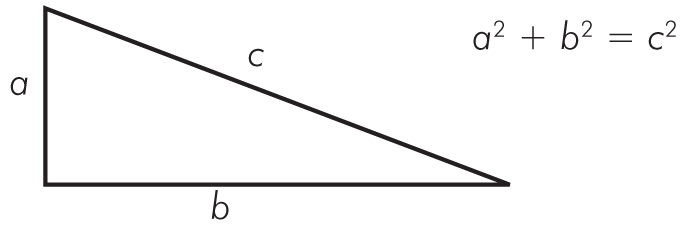
Twierdzenie Pitagorasa
Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
a, b – długości przyprostokątnych
c – długość przeciwprostokątnej
Uwaga!
Stosując twierdzenie Pitagorasa, można obliczyć długość jednego z boków trójkąta prostokątnego, gdy są znane długości dwóch pozostałych boków.
Warto wiedzieć, że…
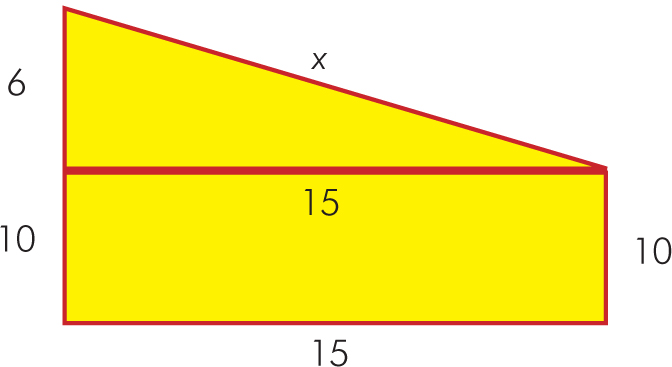
W wielu figurach płaskich poprzez dorysowanie w danej figurze odpowiednich odcinków otrzymujemy trójkąty prostokątne, dla których można stosować twierdzenie Pitagorasa:
Musisz znać i stosować…
Twierdzenie odwrotne do twierdzenia Pitagorasa.
Jeżeli w trójkącie suma kwadratów długości dwóch krótszych boków jest równa kwadratowi długości najdłuższego boku, to trójkąt jest prostokątny.
Zadanie 1.
a) Przyprostokątne trójkąta prostokątnego mają długości 1 i 2. Oblicz długość przeciwprostokątnej tego trójkąta.
b) Jedna z przyprostokątnych trójkąta prostokątnego ma długość 7,5 cm, a długość przeciwprostokątnej wynosi 12,5 cm. Oblicz pole i obwód tego trójkąta.
Rozwiązanie: Wykonajmy rysunek zgodny z treścią zadań i ułóżmy twierdzenie Pitagorasa:
a)
x² = 1² + 2²
x² = 1 + 4
x = √5
Odpowiedź: Długość przeciwprostokątnej wynosi √5.
b)
Mając dane długości przyprostokątnych, można wyliczyć pole i obwód trójkąta:
P = 1/2 · 10 cm · 7,5 cm = 37,5 cm²
L = 7,5 cm + 10 cm + 12,5 cm = 20 cm
Odpowiedź: Pole trójkąta wynosi 37,5 cm², a obwód 20 cm.
Zadanie 2
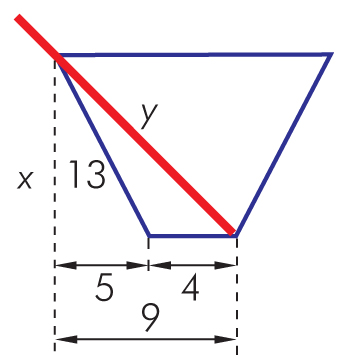
Jaką długość powinna mieć rurka włożona do szklanki, aby – przy takim ułożeniu jak na rysunku – wystawała ze szklanki na mniej więcej 3 cm? (Wymiary na rysunku podano w centymetrach).
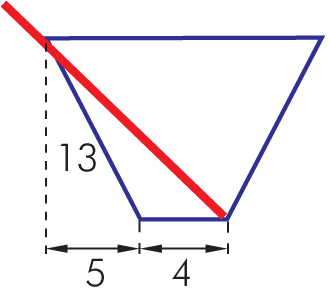
Rozwiązanie: Wprowadzamy dodatkowe oznaczenia na rysunku:
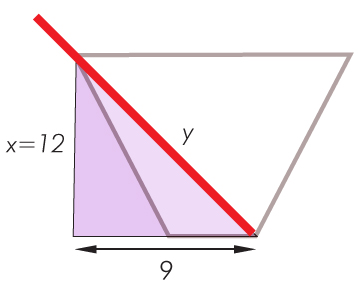
Musimy dwukrotnie skorzystać z twierdzenia Pitagorasa: najpierw dla trójkąta prostokątnego o bokach x, 5 i 13.
x² + 5² = 13²
x² = 169 – 25
x = 12 [cm]
Teraz układamy twierdzenie Pitagorasa dla trójkąta prostokątnego o bokach x = 12, 9 i y.
y² = 12² + 9²
y² = 144 + 81
y = 15 [cm]
Ponieważ poza szklankę wystają 3 cm rurki, więc długość całej rurki wynosi 15 cm + 3 cm = 18 cm.
Odpowiedź: Rurka powinna mieć długość około 18 cm.
Zadanie 3
Sprawdź, czy trójkąt o bokach 2, 4√2, 6 jest prostokątny.
Rozwiązanie: Stosujemy twierdzenie odwrotne do twierdzenia Pitagorasa.
Twierdzenie odwrotne do Twierdzenia Pitagorasa: Jeżeli suma kwadratów dwóch krótszych boków w trójkącie jest równa kwadratowi najdłuższego boku to ten trójkąt jest prostokątny.
Ponieważ 2², (4√2)²= 32, 6² = 36, a 4 + 32 = 36, więc prawdziwa jest równość 2² + (4√2)² = 6².
Odpowiedź: Trójkąt o bokach 2, 4√2, 6 jest prostokątny.
Zadanie 4
Drabina opiera się o budynek na wysokości 3 m. Jej dolny koniec jest odsunięty od ściany o 2 m. Jaka jest długość drabiny?
A. √2 m
B. √10 m
C. √5 m
D. √13 m
Rozwiązanie
Oznaczmy przez x długość drabiny i wykonajmy rysunek pomocniczy.
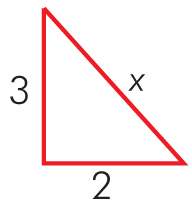
Stosujemy twierdzenie Pitagorasa:
x² = 3² + 2²
x = √13 [m]
Odpowiedź: D
Zadanie 5
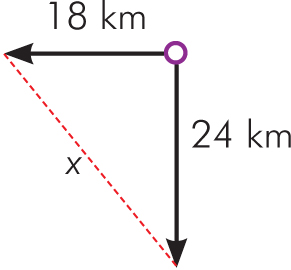
Ze statku stojącego na kotwicy spuszczono dwie szalupy. Pierwsza popłynęła na zachód z prędkością 9 km/h, druga na południe z prędkością 12 km/h. Jaka odległość będzie dzieliła te szalupy po upływie dwóch godzin?
Rozwiązanie: Ze wzoru na prędkość obliczymy najpierw drogi pokonane przez te szalupy:
S1 = 9 · 2 h = 18 km
S2 = 12 · 2 h = 24 km
Wykonamy teraz pomocniczy rysunek, uwzględniając to, że pierwsza szalupa popłynęła na zachód, a druga na południe:
Z twierdzenia Pitagorasa wynika, że x² = 182 + 242, czyli x² = 900 i dalej x = 30 [km].
Odpowiedź: Po dwóch godzinach odległość między szalupami będzie wynosiła 30 km.
Zadanie na szóstkę
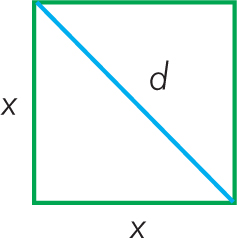
Przekątna kwadratu jest o 2 cm dłuższa od jego boku. Jaki obwód ma ten kwadrat?
Rozwiązanie: Oznaczmy przez x długość boku kwadratu.Wtedy długość przekątnej można zapisać jako d = x + 2
Wykorzystujemy twierdzenie Pitagorasa: x² + x² = d². Stąd po przekształceniu d = x√2.
U nas x√2 = x + 2. Przenosimy wyrazy z x na lewą stronę i wyłączamy x przed nawias x(√2 – 1) = 2. Teraz dzielimy obustronnie przez wyrażenie w nawiasie, a potem korzystając ze wzoru skróconego mnożenia, usuwamy niewymierność:
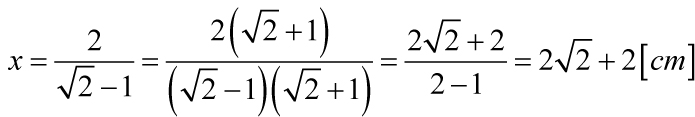
Ponieważ znamy już długość boku kwadratu, więc możemy obliczyć jego obwód:
L = 4 · (2√2 + 2) = 8√2 + 8 = 8(√2 + 1) [cm]
Odpowiedź: Obwód kwadratu wynosi 8(√2 + 1) cm.
Zadanie 6
Pan Jan uzyskał pozwolenie na tymczasowe doprowadzenie energii elektrycznej do swojego placu budowy. Odległość między słupem trakcji elektrycznej i słupem na placu budowy jest równa 15 m, a wysokości przyłączeń przewodu elektrycznego na słupach są równe odpowiednio 16 m i 10 m. W promocji można było kupić zwoje przewodów o długościach: 15 m, 16 m, 17 m i 18 m. Pan Jan wykorzystał okazję i kupił zwój dłuższy od odległości między obydwoma miejscami przyłączenia przewodu o mniej niż metr. Oblicz długość przewodu kupionego przez pana Jana. Napisz obliczenia.
Rozwiązanie:
Po dokładnej analizie zadania wykonujemy rysunek:
x – odległość przyłącza na domu od przyłącza na słupie
Dla powstałego trójkąta prostokątnego układamy twierdzenie Pitagorasa:
x² = 6² + 15²
x = √261 [m]
Ponieważ 16 < 261 < 17, a zwój miał być dłuższy od odległości między miejscami przyłączenia przewodu o mniej niż metr, więc pan Jan kupił przewód o długości 17 m.
Odpowiedź: Długość przewodu kupionego przez pana Jana wynosi 17 m.
Zadanie 7
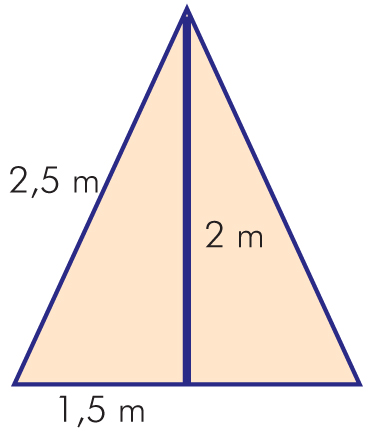
Przy wejściu do namiotu ustawiono maszt o długości 2 m. Czy maszt ten ustawiono pionowo?
Powtórz!
Twierdzenie odwrotne do twierdzenia Pitagorasa
Jeśli w trójkącie suma kwadratów długości dwóch krótszych boków jest równa kwadratowi długości najdłuższego boku,
to trójkąt jest prostokątny.
Rozwiązanie:
Jeżeli maszt ustawiono pionowo, to powstałe trójkąty są prostokątne. Korzystamy z twierdzenia odwrotnego do twierdzenia Pitagorasa.
Obliczamy kwadraty długości boków:
2² = 4,
1,5² = 2,25,
2,5² = 6,25.
Można stwierdzić, że 4 + 2,25 = 6,25, czyli 2² + 1,5² = 2,5² – trójkąt jest prostokątny.
Odpowiedź: Maszt został ustawiony pionowo.
Zadanie 8
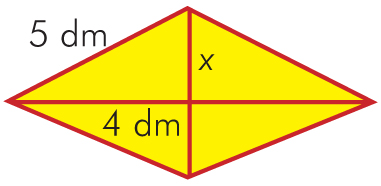
Latawiec wykonany przez Marka ma kształt rombu, w którym długość boku wynosi 5 dm, a jedna z przekątnych
ma długość 8 dm. Oblicz długość drugiej przekątnej tego rombu.
Uwaga!
Romb to taki równoległobok, który ma wszystkie boki równe.
W rombie przekątne:
- są prostopadłe,
- dzielą się na połowy,
- są dwusiecznymi kątów wewnętrznych,
- są osiami symetrii.
Zauważ!
Jeżeli w rombie narysujemy obydwie przekątne, to czworokąt ten zostaje podzielony na cztery przystające trójkąty prostokątne.
Rozwiązanie:
Ponieważ cała przekątna ma długość 8 dm, więc jej połowa ma 4 dm.
x – połowa długości drugiej przekątnej
x² + 4² = 5², czyli x = 3 dm.
Odpowiedź: Długość drugiej przekątnej rombu wynosi 6 dm.
Poćwicz
1. Jaką długość powinna mieć rurka, aby wystawała ze szklanki około 4 cm?

A. ok. 9 cm
B. ok. 13 cm
C. ok. 17 cm
D. ok. 21 cm
2. Który z trójkątów o podanych długościach boków jest prostokątny?
A. √6, √10, 4
B. 1, 2, 3
C. √3, 4, √7
D. 9, 3, 3
3. W okręgu o średnicy 20 cm narysowano cięciwę długości 12 cm. Odległość tej cięciwy od środka okręgu wynosi:
A. 2 cm
B. 4 cm
C. 8 cm
D. 64 cm
4. Wzdłuż przekątnej prostokątnego trawnika o bokach 24 m i 18 m poprowadzono ścieżkę. Długość tej ścieżki wynosi:
A. 30 m
B. 42 m
C. 15 m
D. 6 m
5. Trzy kutry rybackie stoją na morzu zakotwiczone w miejscach K, L, M. Odległość między statkami K i L jest równa:
A. 400 m
B. 200 m
C. 100 m
D. 50 m
Odpowiedzi:
1. C, 2. A, 3. C, 4. A, 5. B