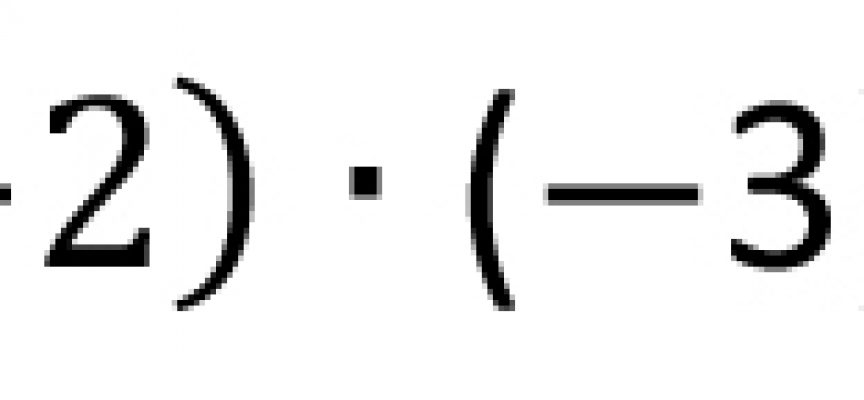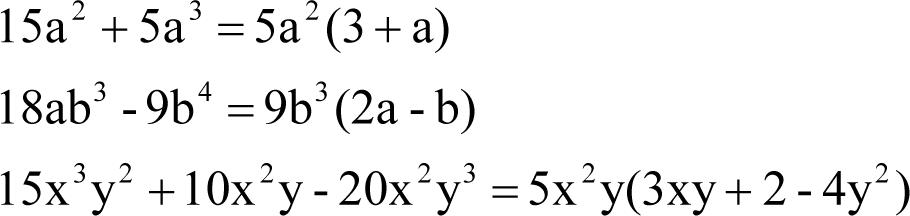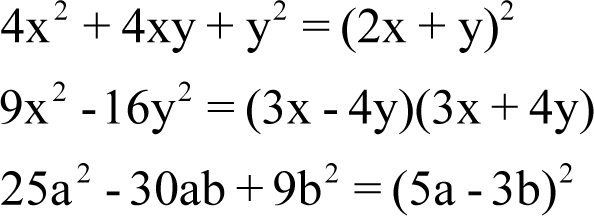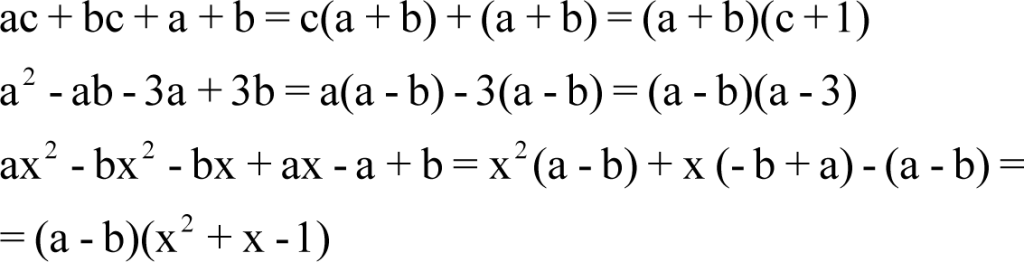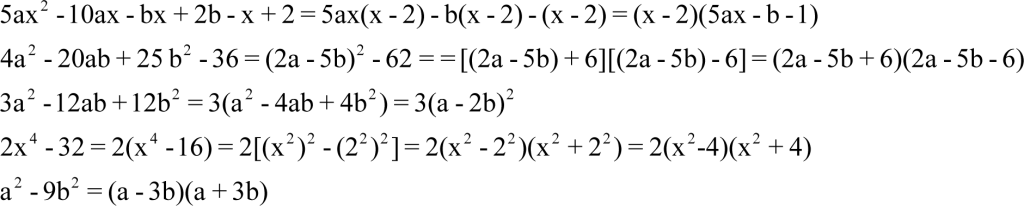Wyrażenia literowe oraz wzory skróconego mnożenia

Wyrażenie

Wyrażeniem (w sensie matematycznym) nazywamy pojedynczą liczbę lub zmienną literową, albo kilka liczb czy zmiennych literowych połączonych znakami działań. Np.:

5; –a; 4 + x; 6(y + 1)²

Wyrażenia dzielimy na:

arytmetyczne – jeśli występują tylko elementy zbiorów liczbowych;
5 +2; 8 – (–4); 10 – 6; 10 2; 5(2 + 6 – 5) – to wyrażenia arytmetyczne
algebraiczne (lub literowe) – jeśli występuje chociażby jedna zmienna literowa.
2x; 5x – 9; 2x + 6y; 4(a + p)² – to wyrażenia algebraiczne

Każde wyrażenie, czy to arytmetyczne, czy też algebraiczne, posiada swoją nazwę, którą bierze od ostatniego wykonywanego działania, np.:

2x – y – różnica iloczynu 2 przez x i zmiennej y;
a² + b² – suma kwadratów zmiennych a i b;
2(x + y)³ – iloczyn liczby 2 i sześcianu sumy zmiennych x i y;
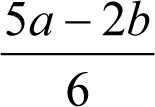– iloraz, którego licznik jest różnicą iloczynów 5 przez a i 2 przez b a mianownik liczbą 6

Zapamiętaj!
Wyrażenie algebraiczne nie posiada określonej wartości liczbowej, dopóki nie wstawimy w miejsce zmiennych konkretnych liczb. Wyrażenie algebraiczne zamienia się wtedy w wyrażenie arytmetyczne o ustalonej wartości liczbowej. Np.

(5a² – 2)·b dla a = 1 i b = –2, posiada wartość:

(5a² – 2) · (–2) = (5 – 2) · (–2) = 3 · (–2) = –2

To samo wyrażenie dla a = –2 i b = 3, posiada wartość:

(5 · (–2)² – 2) · 3 = (5 · 4) · –2) · 3 = (20 – 2) · 3 = 18 · 3 = 54

Prostym wyrażeniem algebraicznym jest jednomian.

Jednomian

Jednomianem nazywamy iloczyn czynników cyfrowych lub literowych, albo pojedynczy znak liczby, czy zmiennej literowej. Np.:

Liczbę występującą w jednomianie nazywa się współczynnikiem liczbowym jednomianu.
Uwaga! Każdy jednomian musi mieć współczynnik liczbowy. W przypadku, gdy nie jest on zapisany, to znaczy, że jest równy 1.

Bardzo ważną czynnością jest uporządkowanie jednomianu.

Uporządkować jednomian, to znaczy:

Wymnożyć wszystkie czynniki cyfrowe,
Ułożyć zmienne literowe w kolejności alfabetycznej,
Zastąpić iloczyn jednakowych zmiennych literowych, ich potęgą,

Uporządkujmy jednomian

1. mnożymy czynniki cyfrowe ustalając współczynnik całego jednomianu
2. zmienne układamy w kolejności alfabetycznej
a · a · a²· b² · b
3. jednakowe czynniki zastępujemy potęgą
a · a · a²· b² · b = a⁴b³

Zatem uporządkowany jednomian ma postać ładniejszą niż początkowy, a mianowicie -2a⁴b³

Jednomiany można dodawać, odejmować, mnożyć i dzielić.

Mnożąc dwa lub więcej jednomianów, otrzymamy jednomian np.:

jednomian mn

Ułamek algebraiczny

Dzieląc dwa jednomiany otrzymamy ułamek algebraiczny, np.

Ułamek ma sens liczbowy tylko wtedy, gdy jego mianownik nie jest równy zero, więc w naszym przykładzie nie wolno podstawiać zamiast d zera,

Piszemy: jednomian dziel ; d ≠ 0

Ułamek algebraiczny, to szersze pojęcie niż iloraz dwóch jednomianów. W jego liczniku i mianowniku mogą występować nie tylko jednomiany. Mogą to być wyrażenia algebraiczne i wtedy ułamek przybiera bardziej złożoną postać, np.:

Ułamki algebraiczne można

skracać, np.: dzieląc licznik i mianownik przez taki sam jednomian (w tym wypadku 2xyz²)

rozszerzać: mnożąc jego licznik i mianownik przez taki sam jednomian (w tym przypadku 3p).

Ułamki algebraiczne można także:

dodawać
odejmować
mnożyć
dzielić

stosując te same prawidła jak w działaniach na ułamkach arytmetycznych, np.:

1.

Warto zapamiętać, że:

I. wartość ułamka algebraicznego równa jest zeru, gdy jego licznik równy jest zeru. Np.

, gdy x = 0, wtedy podstawiając x = 0 mamy:

II. ułamek traci sens liczbowy, gdy jego mianownik równy jest zeru. Np.

, gdy x = 5, wtedy : dzielenie nie jest wykonalne czyli ułamek nie ma sensu liczbowego.

Suma algebraiczna

Dodając lub odejmując jednomiany otrzymamy sumę algebraiczną. Dodawane jednomiany nazywamy wyrazami sumy algebraicznej

W sumach algebraicznych można dodawać lub odejmować tylko wyrazy podobne tzn. takie, które mają takie same zmienne literowe w tej samej potędze, a różnią się jedynie współczynnikami cyfrowymi. Mówimy wtedy, że dokonaliśmy redukcji wyrazów podobnych.

Polega ona na tym, że dodajemy lub odejmujemy współczynniki cyfrowe wyrazów, a zmienne literowe zostają bez zmiany. Np.:

5a² + 4ab – 6a + 12a² – 7ab + 4a – ab = (5 + 12)a² + (4 – 7 – 1)ab + (–6 + 4)a = 17 a² – 4ab – 2a

Sumy algebraiczne można:

dodawać – otrzymujemy w wyniku sumę algebraiczną
odejmować – otrzymujemy w wyniku sumę algebraiczną
mnożyć – otrzymujemy w wyniku sumę algebraiczną
dzielić – otrzymujemy ułamek algebraiczny lub sumę algebraiczną

1. Przy dodawaniu sum algebraicznych opuszczamy nawiasy pozostawiając znaki wyrazów dodawanych bez zmiany i wykonujemy redukcję wyrazów podobnych doprowadzając do najprostszej postaci, np.:

7a + [4b + (2a + 3b)] + (–8a + 5b) = 7a + [4b + 2a + 3b] – 8a + 5b = 7a + 4b + 2a + 3b – 8a + 5b = a + 12b

2. Przy odejmowaniu sum algebraicznych opuszczamy nawiasy pamiętając o zmianie znaków wyrazów w nawiasie, przed którym stał minus, a dalej redukujemy wyrazy podobne również doprowadzając do najprostszej postaci, np.:

– 4x – (2x – 3y) – (–7y + 5x – 2) – (– 9x + 4y – 3) = – 4x – 2x + 3y + 7y – 5x + 2 + 9x – 4y + 3= – 2x + 6y + 5

3. Mnożąc sumę algebraiczną przez jednomian mnożymy po kolei każdy wyraz tej sumy przez dany jednomian i redukujemy wyrazy podobne, jeśli to możliwe, np.:

a) –3xy · (–2x – 3y + z + 2) = 6x²y + 9xy² – 3xyz – 6xy
b) 6p · (2m – 3n) + (5n – 1)3p = 12mp – 18np + 15np – 3p = 12mp – 3np – 3p

4. Dzieląc sumę algebraiczną przez jednomian wykonujemy dzielenie po kolei każdego wyrazu tej sumy przez dany jednomian i redukujemy wyrazy podobne, jeśli jest to możliwe, np.:

(20a² – 10ab + 5a³b) : 5a = 4a – 2b + a²b

5. Mnożąc sumy algebraiczne przez siebie musimy wymnożyć każdy wyraz jednej sumy przez każdy wyraz drugiej sumy i otrzymane wyrazy zredukować, jeśli jest to możliwe, np.:

(a + b) · (c + d) = ac + ad + bc + bd
L P
Interpretacja geometryczna tego mnożenia jest następująca:

Lewa strona L, to pole prostokąta, którego długości boków wynoszą
(a + b) i (c + d)
Prawa strona P, to suma pól części składowych tego prostokąta
czyli ac + ad + bc + bd

Przykład:

Szczególnym przypadkiem mnożenia sum algebraicznych jest mnożenie jednakowych czynników, np.: (a + b) · (a + b) czyli (a + b)2. W interpretacji geometrycznej wygląda to tak:

Pole kwadratu o boku (a + b) czyli (a + b)² jest równe sumie pól kwadratów a² i b² oraz prostokątów ab i ab, stąd

(a + b)² = a² + ab + ab + b² czyli (a + b)² = a² + 2ab + b²

Jest to wzór należący do wcale niemałej grupy wzorów skróconego mnożenia, które to, jak sama nazwa wskazuje, ułatwiają mnożenie.

Następne wzory z tej rodziny używane w szkole to:

(a – b)² = a² – 2ab + b²
(a + b) · (a – b) = a² – b²

Przykłady:
a) (x + 3)2 = x² + 2x .3 + 3² = x2 + 6x +9
b) (x -)2 = x2 + 2. x . + ()2 = x2 + x +
c)
d) (2x – 3)(2x + 3) = 4×2 – 9
e) (x + 3y)(x – 3y) + (x + 2y)2 – (2×2 + 5y) =
= x2 – 9y2 + x2 + 4xy + 4y2 – 2×2 – 5y) = 4xy – 5y2 -5y
f) 512 = (50 + 1)2 = 502 + 2 . 50 . 1 + 12 = 2500 + 100 + 1 = 2601
g) 492 = (50 – 1)2 = 2500 – 100 + 1 = 2401
h) 51 . 49 = (50 + 1)(50 – 1)= 2500 – 1 = 2499

Ćwiczenie:

Oblicz wartość liczbową wyrażenia:
dla y = i x =

1. Wykonuję mnożenie sum algebraicznych oraz stosuję wzory skróconego mnożenia.
2. Opuszczam nawiasy w liczniku i stosuję redukcję wyrazów podobnych
3. Podstawiam wartości liczbowe zmiennych i otrzymuję:
Do działań na sumach algebraicznych stosuje się te same prawa co do działań na liczbach rzeczywistych, a mianowicie:
* w dodawaniu – przemienność , łączność
* w mnożeniu – przemienność, łączność, rozdzielność
* w dzieleniu – rozdzielność

Prawo rozdzielności ma również zastosowanie w wyłączaniu czynnika poza nawias. Jest to sposób zamiany sumy algebraicznej na iloczyn (postać iloczynowa jest ważną postacią wyrażenia algebraicznego), np.: