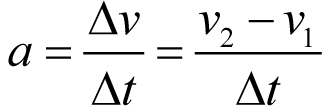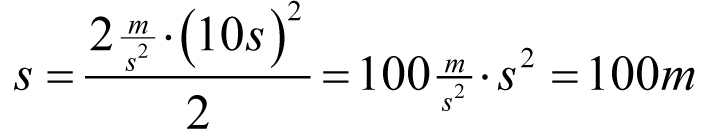1. Co to jest przyspieszenie?
Przyspieszenie jest wielkością fizyczną, która jest miarą zmiany prędkości ciała. Co się może zmieniać? Wartość prędkości, czyli szybkość (ciało przyspiesza lub zwalnia), oraz kierunek prędkości (ciało skręca). Wszystkie te rodzaje zmian prędkości są opisywane przez jedną wielkość fizyczną – przyspieszenie. Bardziej precyzyjna definicja przyspieszenia pozwoli nam je obliczyć:
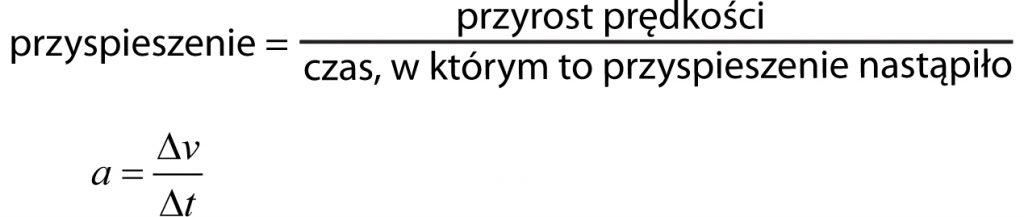
Przyspieszenie to stosunek zmiany (przyrostu) prędkości do czasu, w którym ta zmiana nastąpiła.
Przyrosty czy zmiany oznaczamy w fizyce grecką literą Δ (delta).
Zatem definicję przyspieszenia możemy symbolicznie zapisać tak:
to zmiana prędkości, a Δt – czas (odstęp albo przedział czasu), w którym nastąpiła zmiana prędkości.
Zauważ!
Zmiana prędkości, tak samo jak prędkość, jest wielkością wektorową. Jeśli ciało porusza się po linii prostej, czyli nie zmienia się kierunek jego ruchu, to przyspieszenie wiąże się jedynie ze zwiększaniem lub zmniejszaniem szybkości. Jak w takim wypadku obliczyć w praktyce wartość przyspieszenia? W przypadku ruchu po prostej wektorowy charakter przyspieszenia nie ma wielkiego znaczenia. Definicję przyspieszenia możemy uprościć:
Aby obliczyć wartość przyspieszenia, należy od szybkości końcowej odjąć początkową i wynik podzielić przez czas, w którym nastąpiła zmiana szybkości.
2. Jaka jest jednostka przyspieszenia?
Zmiana prędkości jest wyrażona w metrach na sekundę, a czas w sekundach. Wobec tego jednostką przyspieszenia jest metr na sekundę i jeszcze raz na sekundę. Krócej: metr na sekundę kwadrat. Zapiszmy to symbolicznie:
Przyspieszenie wynoszące ![]() oznacza, że w każdej sekundzie prędkość ciała zwiększa się o 1m/s.
oznacza, że w każdej sekundzie prędkość ciała zwiększa się o 1m/s.
3. Jaki ruch nazywamy jednostajnie przyspieszonym?
Taki, w którym przyspieszenie jest stałe, a szybkość rośnie. Inaczej: taki ruch, w którym szybkość ciała wzrasta równomiernie. Wyobraź sobie, że jedziesz samochodem i co 2 s notujesz jego szybkość:
Zauważ!
Co każde 2 s szybkość rośnie równomiernie o 1 m/s. Możesz na podstawie tej tabeli obliczyć przyspieszenie pojazdu. Bierzemy jakiś przedział czasu, np. między 4 s i 8 s, odczytujemy, jakie szybkości odpowiadają tym momentom (2 m/s i 4 m/s), obliczamy zmianę szybkości, odejmując od późniejszej wartości szybkości wartość wcześniejszą i dzielimy przez czas, jaki upłynął między tymi dwoma momentami:
Przyspieszenie obliczone dla innych przedziałów czasu jest dokładnie takie samo. Przyspieszenie jest po prostu stałe, a ruch jest jednostajnie przyspieszony.
Skojarz!
Przykładem ruchu jednostajnie przyspieszonego jest spadanie ciał. Ciała, niezależnie od masy, spadają z przyspieszeniem g = 9,81 m/s2 (przyspieszenie oznacza się tu – dla wyróżnienia – nietypowo literą g). W zadaniach szkolnych często przyjmuje się przybliżoną wartość przyspieszenia ziemskiego (tak się je nazywa) g = 10 m/s2. Oznacza to, że spadające ciało zwiększa swą szybkość o 10 m/s w ciągu każdej kolejnej sekundy.
4. Jak zmienia się szybkość w ruchu jednostajnie przyspieszonym?
Zależność szybkości od czasu w ruchu jednostajnie przyspieszonym opisuje prosty wzór:
szybkość = przyspieszenie · czas ruchu
symbolicznie: v = at
Przykład:
Ciało poruszało się przez 5 sekund z przyspieszeniem 2 m/s2. Jaką szybkość osiągnęło ciało po tych 5 s?
Korzystamy z przytoczonego wzoru:
v = at = 2 m/s2 · 5 s = 10 m/s
Zwróć uwagę na rachunek jednostek.
5. Jaką drogę przebywa ciało w ruchu jednostajnie przyspieszonym?
Drogę przebywaną w ruchu jednostajnie przyspieszonym można obliczyć ze wzoru:
s – droga
a – przyspieszenie
t – czas ruchu
Przykład:
Oblicz drogę przebytą przez ciało poruszające się ruchem jednostajnie przyspieszonym z przyspieszeniem a = 2 m/s2 Czas ruchu wynosi t = 4 s.
Rozwiązanie:
Korzystamy z naszego wzoru:
6. Jak wygląda wykres zależności szybkości od czasu w ruchu jednostajnie przyspieszonym?
Szybkość w takim ruchu rośnie proporcjonalnie do czasu: v = at. Czy pamiętasz, jak wygląda wykres proporcjonalności? Tak? To dobrze.
Uwaga! Kąt nachylenia tego wykresu do poziomej osi jest zależny od przyspieszenia. Im większe przyspieszenie, tym większy kąt. Z wykresu łatwo możemy odczytać, że szybkość równomiernie rośnie. Jeśli podzielimy oś czasu na równe części, to przekonamy się, że odpowiadają im równe przyrosty szybkości.
Takich zadań spodziewaj się na egzaminie!
Zadanie zamknięte
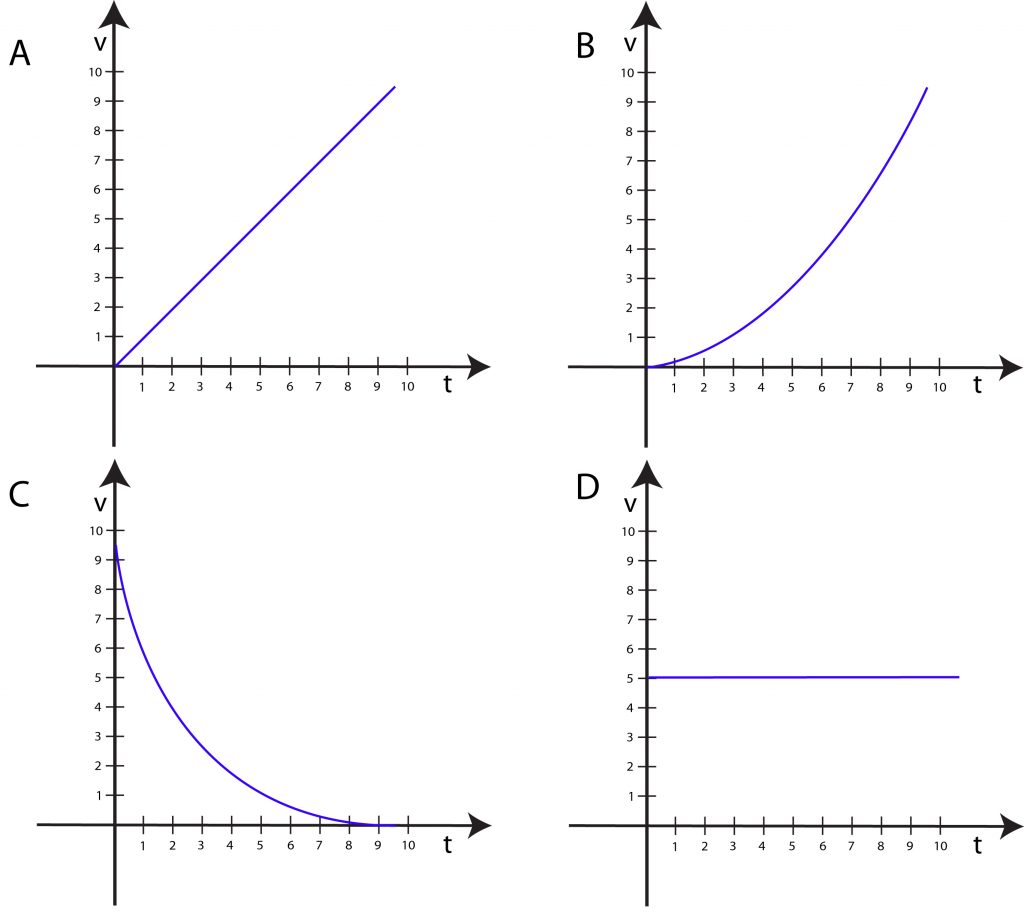
Michał podlewał kwiatki stojące na parapecie. Podczas podlewania potrącił jedną z doniczek i ta spadła z piątego piętra. Który z wykresów przedstawia zależność prędkości doniczki od czasu jej spadania? (Opór powietrza jest na tyle niewielki, że możemy go pominąć).
Rozwiązanie
Jakim ruchem jest swobodne spadanie ciał? Oczywiście jednostajnie przyspieszonym (o ile opór powietrza jest mały). Który wykres przedstawia ruch jednostajnie przyspieszony? Wiemy, jakim wzorem wyraża się prędkość w ruchu jednostajnie przyspieszonym: v = at. Jakiego typu jest to funkcja? Czas i prędkość to zmienne, zaś przyspieszenie jest stałe. Jest to więc funkcja postaci y = ax, czyli funkcja liniowa. Wykresem takiej funkcji jest wykres A.
Albo inaczej. W ruchu jednostajnie przyspieszonym prędkość rośnie równomiernie. Znaczy to, że w ciągu każdej kolejnej sekundy prędkość rośnie o tyle samo. W którym przypadku tak jest? Na wykresie D prędkość jest stała, nie rośnie. Wykres C pokazuje malejącą prędkość – tym bardziej to nie to. Wzrost prędkości w czasie pokazują wykresy A i B, ale tylko w przypadku A jest to wzrost jednostajny, równomierny.
Zadanie otwarte
Samochód ruszył z miejsca i w ciągu 10 s osiągnął szybkość 72 km/h. Jakie było średnie przyspieszenie samochodu? Jaką drogę przejechał samochód w tym czasie?
Rozwiązanie
Pierwszą czynnością – wstępną – będzie doprowadzenie do zgodnych jednostek. Zamieńmy kilometry na godzinę na metry na sekundę.
By obliczyć wartość przyspieszenia, korzystamy z jego definicji
Przyrost szybkości to 20 m/s. Samochód rozpędził się od zera do takiej właśnie szybkości. Czas, w jakim to zrobił, to 10 s. Obliczenie przyspieszenia jest już łatwe:
Przebytą drogę obliczamy ze wzoru
Dlaczego tego? Dlatego, że to jest właśnie wzór na drogę w ruchu jednostajnie przyspieszonym w sytuacji, gdy prędkość początkowa jest równa zeru.
Odpowiedź: Przyspieszenie pojazdu wyniosło a = 2 m/s2, przebyta droga to 100 m.