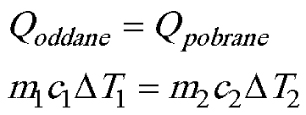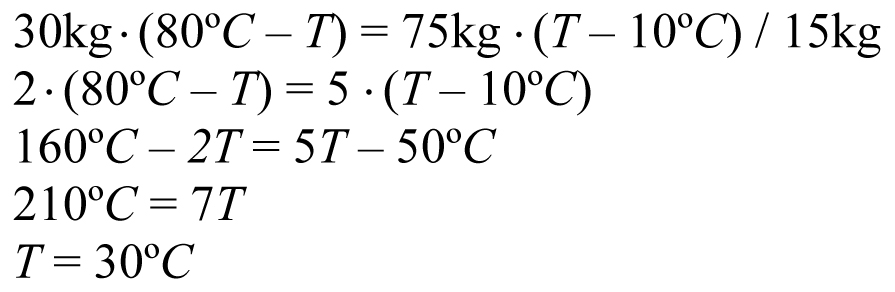1. Co to jest ciepło właściwe?
Wyobraź sobie, że podgrzewasz równe masy (np. po 10 gramów) wody i rtęci. Chcesz, by temperatury obu substancji wzrosły o, powiedzmy, 10ºC. Ile ciepła należy w tym celu dostarczyć obu substancjom? Czy po tyle samo? Może odpowiesz, że tak, skoro jednakowe są masy, a i przyrost temperatury taki sam. Nie, nie tyle samo! Okazuje się, że woda pochłonie znacznie więcej ciepła niż rtęć. Substancje różnią się ilością ciepła potrzebną do podgrzania jednostki masy o jeden stopień. Mówimy, że różnią się ciepłem właściwym.
Co to jest ciepło właściwe?
Jest to właśnie ilość ciepła potrzebna do ogrzania jednostki masy danej substancji o jednostkę temperatury, czyli na przykład jednego kilograma o jeden kelwin. Ciepło właściwe będziemy oznaczać literą c. Definicję ciepła właściwego można zapisać wzorem:
Q – ciepło potrzebne na ogrzanie
m – masa ciała
∆T – zmiana jego temperatury
Zatem, aby obliczyć ciepło właściwe substancji, należy podzielić ilość pochłoniętego przez zbudowane z tej substancji ciało ciepła przez przyrost temperatury wywołany pochłonięciem ciepła i przez masę ciała. Jednostką ciepła właściwego jest
Popatrz na zestawienie przedstawiającą ciepło właściwe rozmaitych substancji.
Nazwa substancji Ciepło właściwe (J/kg·K)
ołów 130
woda 4200
aluminium 920
para wodna 1020
lód 2100
tlen 920
rtęć 100
Wodór 14 300
Co można odczytać z takiej tabeli?
Na przykład, że ogrzanie kilograma wody o 1 K wymaga 42 razy więcej ciepła niż ogrzanie takiej samej ilości rtęci (też o 1 K)! Albo że aby ogrzać lód, musimy dostarczyć mu mniej ciepła niż wodzie. Także, że łatwiej ogrzać tlen niż wodór itd.
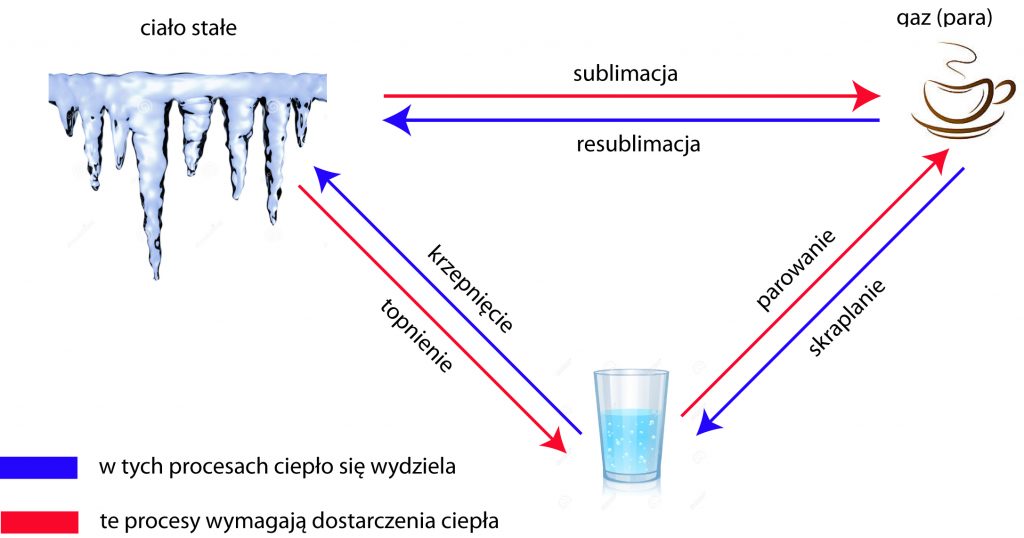
2. Jakie znasz zmiany stanów skupienia?
Zacznijmy od tego, jakie są stany skupienia. Na takie pytanie odpowie nawet dziecko: stały, ciekły i gazowy zwany też lotnym. Jest to oczywiście uproszczenie rzeczywistości, bo niektórych substancji nie sposób zakwalifikować do żadnej z tych grup.
Dostarczając odpowiednią ilość energii, można z ciała stałego zrobić ciecz lub gaz. Odebranie ciepła spowoduje skroplenie gazu albo zestalenie cieczy. Opisane powyżej zjawiska noszą nazwę zmian stanu skupienia. Rysunek wyjaśnia, jakie mamy zmiany stanów skupienia i jak się one nazywają.
By stopić lub odparować masę substancji, musimy dostarczyć jej pewną ilość ciepła. Ile? To zależy od rodzaju substancji i jej masy. Można wprowadzić pojęcie ciepła topnienia lub parowania. Ciepło topnienia (parowania), to ilość ciepła potrzebna do stopienia (wyparowania) jednego kilograma substancji w stałej temperaturze.
ct – ciepło topnienia
Q – ilość ciepła
m – masa
cp – ciepło parowania
Q – ilość ciepła
m – masa
3. Jaki wpływ ma wzrost temperatury na rozmiary i objętość ciał?
Większość ciał zwiększa swe rozmiary i objętość, gdy podnosimy ich temperaturę. Zjawisko to nosi nazwę temperaturowej rozszerzalności ciał. Dlatego właśnie druty energetyczne latem zwisają luźno, a zimą są bardziej napięte. Stalowy pręt, którego początkowa długość wynosi 1 m, gdy podgrzejemy go o 100oC, wydłuży się o 1 mm, aluminiowy o 3 mm.
Woda jest pod tym względem (innymi zresztą też) substancją wyjątkową. Powyżej temperatury 4oC rozszerza się tak samo jak inne substancje, ale poniżej tej temperatury kurczy się, gdy temperatura wzrasta. Najmniejszą objętość ma więc woda w temperaturze 4oC. Ma to duże znaczenie dla żywych istot w zbiornikach wodnych w czasie zimy.
4. Co możemy obliczyć z równania bilansu cieplnego?
Przede wszystkim odpowiedzmy sobie, co to jest równanie bilansu cieplnego. Jeśli przekształcimy wzór
to otrzymamy wyrażenie na ilość pobranego lub oddanego (zależy, czy temperatura rośnie, czy maleje) ciepła: Q = mcΔT.
Wyobraźmy sobie teraz, że dwa ciała (na przykład zimna i ciepła woda, które mieszamy w wannie) biorą udział w wymianie ciepła. Jedno z nich ciepło oddaje (to o wyższej temperaturze), a drugie pobiera (zimniejsze). Równanie bilansu mówi, że ciepło oddane przez jedno ciało równa się ciepłu pobranemu przez drugie z ciał. Jest to więc w gruncie rzeczy jeszcze jedna forma zasady zachowania energii. Jak widziSZ, to podstawowe prawo fizyki wciska się wszędzie. Oto równanie bilansu cieplnego dla dwóch ciał:
A teraz przykład zastosowania tego równania.
Przykład (i zarazem egzaminacyjne zadanie otwarte)
Marzena chce wziąć kąpiel. Wlała więc 30 litrów gorącej wody o temperaturze 80°C oraz 75 litrów wody zimnej o temperaturze 10°C. Najbardziej lubi kąpać się w wodzie o temperaturze 40°C. Czy będzie zadowolona ze swej kąpieli?
Rozwiązanie
Musimy obliczyć końcową temperaturę wody po wymieszaniu gorącej i zimnej i wyrównaniu temperatur. Na pewno wiesz, że 30 litrów waży 30 kilogramów, a 75 l to 75 kg. Mamy więc masę gorącej i zimnej wody. Wypiszmy (tak dla porządku) dane:
m1 = 30 kg
T1 = 80oC
m2 = 75 kg
T2 = 10oC
Szukana jest T – temperatura końcowa mieszaniny.
Policzmy ciepło oddane przez gorącą wodę.
Nie mamy ciepła właściwego wody (choć moglibyśmy je wziąć z tabeli), ale tym się na razie nie przejmujmy. Ile wynosi zmiana temperatury? Jest to różnica między początkową 80ºC a końcową T.
Kolej na ciepło pobrane. W tym przypadku temperatura wzrosła od 10oC do T.
Zatem:
Czy widzisz już, że ciepło właściwe można skrócić? Nie jest nam potrzebne.
Końcowa temperatura wody wyniesie 30oC, więc Marzena nie będzie zadowolona z kąpieli.
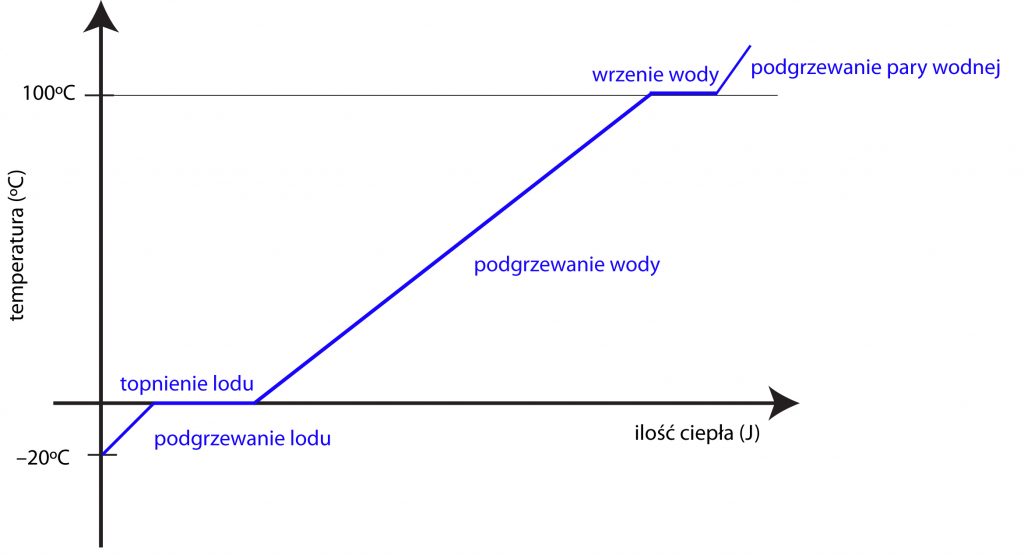
5. Jak wygląda wykres zależności temperatury ciała (np. wody) od ilości dostarczonego ciepła?
Weźmy na przykład wodę. Powiedzmy, że na początku mamy lód o temperaturze –20ºC. Dostarczamy mu równomiernie ciepło. Jego temperatura będzie rosła, aż osiągnie 0ºC. W tej temperaturze lód zaczyna się topić. Dopóki się nie stopi, jego temperatura będzie stała. Po stopieniu lodu woda z niego powstała będzie zwiększać swą temperaturę. Tak będzie, dopóki nie osiągnie 100ºC. W tej temperaturze zaczyna się jej wrzenie. Utrzymując stałą temperaturę, woda będzie gwałtownie parować. Gdy parowanie się skończy, powstała z wody para będzie zwiększać swą temperaturę. To wszystko oczywiście wtedy, gdy cały czas będziemy dostarczać ciepło. A oto wykres omówionych przemian.
Zagadka:
Dlaczego ukośne odcinki wykresu są różnie nachylone do poziomu? Podpowiem: ma to związek z tabelą zamieszczoną na początku.