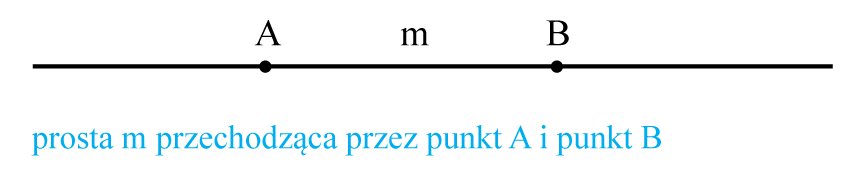PUNKT, PROSTA, PÓŁPROSTA, ŁAMANA, PŁASZCZYZNA

W geometrii istnieją pojęcia pierwotne, których definicji nie jesteśmy w stanie podać. Do takich pojęć należy: PUNKT, PROSTA, PŁASZCZYZNA.Wszystkie inne pojęcia są pochodnymi pierwotnych i dzięki nim definiowane.

Zapamiętaj! Punkt, prosta i płaszczyzna to pojęcia pierwotne, których nie definiujemy.

Punkt

Punkty oznaczamy dużymi literami alfabetu łacińskiego: A, B, C, M, N, K, L, P…
Punkty zaznaczamy za pomocą kropek lub dwóch przecinających się kreseczek.

A • × B
× F • K

Figurą geometryczną nazywamy każdy zbiór punktów.

Prosta

Proste są zbiorem punktów i oznaczamy je małymi literami alfabetu łacińskiego: a, b, c, k, l, m, p…

Prosta nie ma ani punktu początkowego, ani punktu końcowego. Mówimy, że jest nieograniczona.
Jeżeli punkt K leży na prostej a, to zapisujemy: K∈a. Mówimy, że prosta a przechodzi przez punkt K.
Przez dwa różne punkty możemy poprowadzić tylko jedną prostą. Mówimy wtedy, że punkty (np. A i B) wyznaczają prostą.

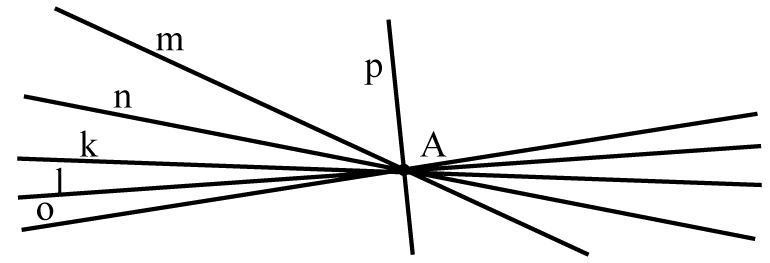
Przez jeden punkt przechodzi nieskończenie wiele prostych.

Pytanie
Ile różnych prostych można poprowadzić przez dwa punkty płaszczyzny?

Odpowiedź
Przez dwa różne punkty przechodzi dokładnie jedna prosta.

Pytanie
Ile różnych prostych można poprowadzić przez trzy punkty płaszczyzny A, B, C?

Odpowiedź
Jeżeli punkty A, B, C są współliniowe, to wyznaczają jedną prostą.

• A
• B • C
Przez trzy niewspółliniowe punkty A, B, C nie można poprowadzić jednej prostej.

Dwie proste

Pytanie
Jakie może być wzajemne położenie dwóch prostych leżących na płaszczyźnie?

Odpowiedź
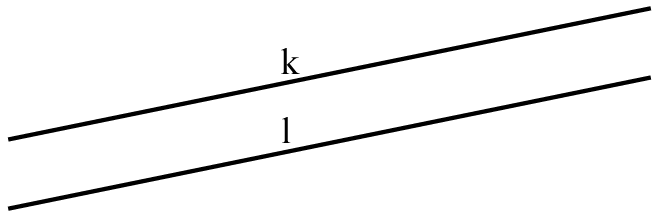
1. Mogą być równoległe, jeśli nie mają punktów wspólnych. zapisujemy to k || l (proste k i l są równoległe).

2. Mogą pokrywają się (leżeć jedna na drugiej) i wówczas mają nieskończenie wiele punktów wspólnych.
Zapisujemy to k = l.

3. Mogą się przecinać i mają wówczas jeden punkt wspólny.

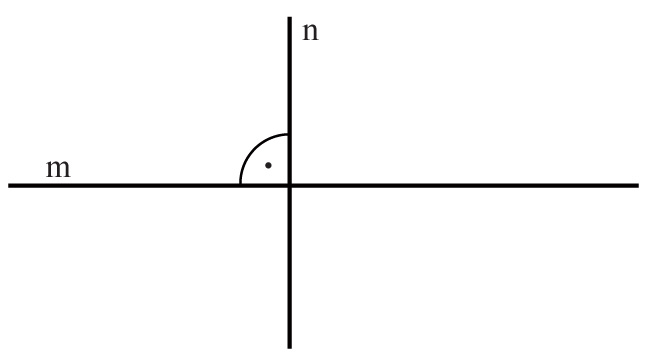
Dwie proste na płaszczyźnie są prostopadłe, jeśli przecinają się pod kątem prostym.
Zapiszemy to:
a ⊥ b – proste a i b są prostopadłe.

Pytanie
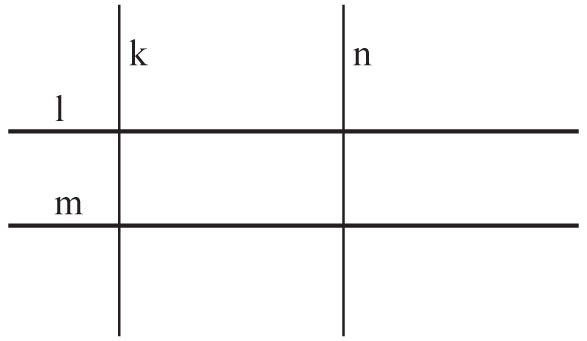
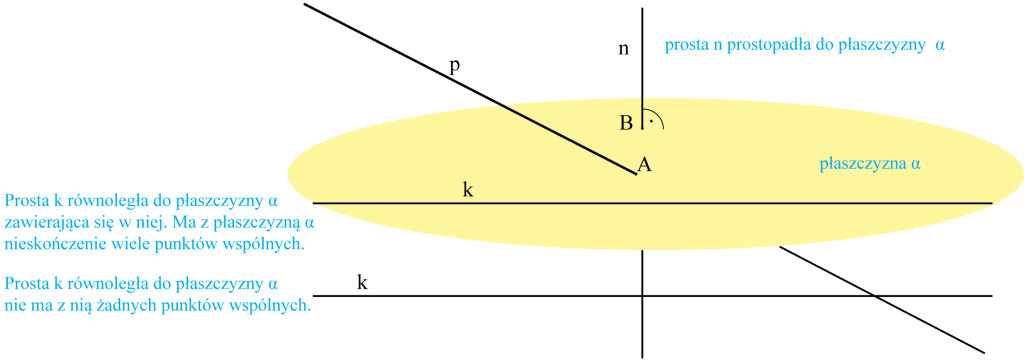
Czy prosta k jest równoległa do prostej n, jeżeli zachodzą zależności:
k⊥l, k⊥m, m⊥n

Odpowiedź
Uzasadnienia dokonamy, wykonując rysunek uwzględniający warunki zadania.

Na tej podstawie łatwo można stwierdzić, że k || n.

Uwaga
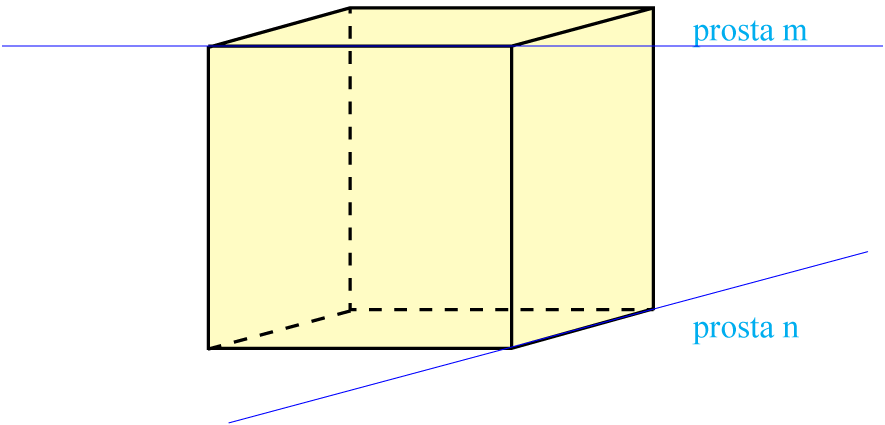
W przestrzeni (nie na płaszczyźnie!) istnieją pary prostych, które ani nie są równoległe, ani się nie przecinają: nazywamy je prostymi skośnymi.
Wyobraź sobie sześcian, w którym przedłużono krawędzie tworząc proste m i n. Proste te nigdy się nie spotkają, ponieważ leżą na różnych płaszczyznach.

Uwaga!
Długość najkrótszego z odcinków łączących dany punkt z punktami prostej nazywamy odległością punktu od prostej.

IMAI – odległość punktu A od prostej p

Półprosta

Dowolny punkt (np. A) leżący na prostej dzieli ją i wyznacza na niej dwie półproste.
Punkt ten nazywamy początkiem półprostej.
Półproste są częścią prostej ograniczone z jednej strony punktem, leżącym na tej prostej.
Półproste te wzajemnie się uzupełniają do prostej (mają jeden punkt wspólny).
Półprosta ma punkt początkowy, ale nie ma punktu końcowego.
Półprostą o początku w punkcie A i przechodzącą przez punkt B oznaczamy jako półprostą .

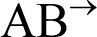Zapis oznacza półprostą o początku w punkcie A przechodzącą przez punkt B.

Pytanie
Jaka figura jest częścią wspólną półprostych i przedstawionych na rysunku?

Odpowiedź
Część wspólna to odcinek AB.

Uwaga!
Dwie półproste o wspólnym początku O dzielą płaszczyznę na dwa obszary. Każdą z dwóch części płaszczyzny zawartą między dwiema półprostymi o wspólnym początku, łącznie z tymi półprostymi, nazywamy kątem.

Odcinek

Odcinek jest to część prostej ograniczonej dwoma punktami, razem z tymi punktami.

Odcinek ograniczony jest z obu stron przez punkty A i B, które nazywamy końcami odcinka.
Odcinek oznaczamy za pomocą punktów granicznych np. AB.
Odcinki możemy też oznaczać małymi literami, np. a, b, c.
Odległość między punktami A i B nazywamy długością odcinka i oznaczamy |AB|.
Jeżeli A = B, to odcinek AB nazywamy odcinkiem zerowym.
Odcinki można dodawać i odejmować.

Zapamiętaj!

Odcinkiem o końcach A i B nazywamy zbiór punktów prostej AB, do którego należą punkty A i B oraz wszystkie punkty leżące między nimi.
O odcinkach AB i CD, które mają równe długości, mówimy, że są przystające. Zapisujemy to w następujący sposób AB = CD.

Symetralna odcinka

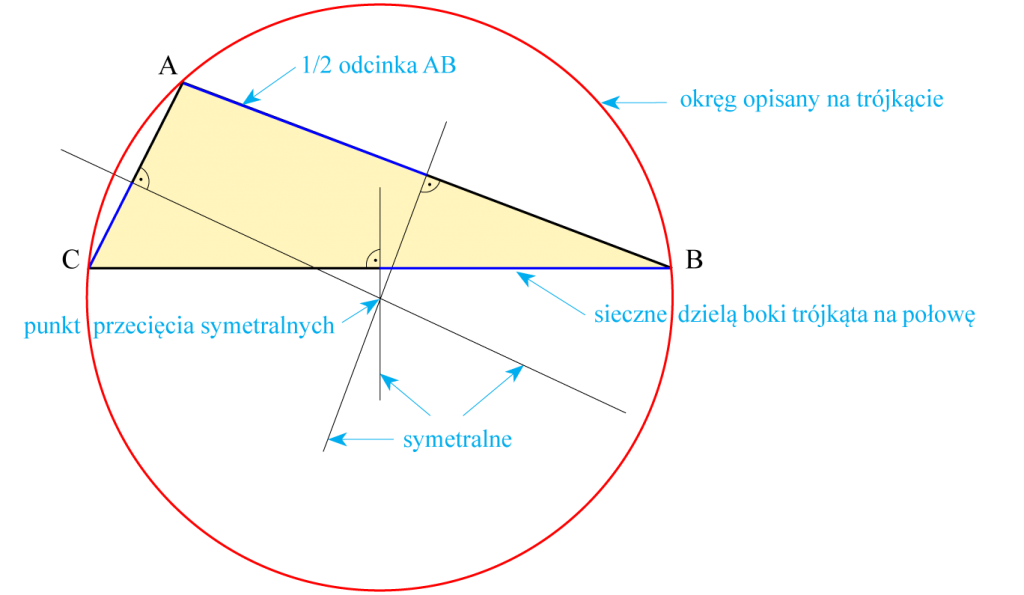
Symetralna odcinka to prosta doń prostopadła i przechodząca przez jego środek.

Symetralne boków trójkąta przecinają się w jednym punkcie; punkt ten jest środkiem okręgu opisanego na tym trójkącie.

Łamana

Łamana jest to figura geometryczna złożona z pewnej ilości punktów połączonych odcinkami w ten sposób, że koniec jednego jest początkiem kolejnego, itd.

Odcinki łamanej nazywamy jej bokami, a ich końce wierzchołkami łamanej.
Jeśli boki łamanej mają wspólne punkty oprócz wierzchołków, łamana nazywa się wiązana.

Zapamiętaj!
Odcinki, z których składa się łamana, nazywamy bokami łamanej, a końce tych odcinków nazywamy wierzchołkami łamanej.

Prosta i płaszczyzna

Płaszczyzna jest to jedno z pierwotnych pojęć geometrii. Możemy wyobrazić ją sobie jako powierzchnię płaską, nieskończenie wielką, nieposiadającą brzegów ani końca.

Płaszczyzny najczęściej oznaczamy małymi literami alfabetu greckiego: α, β, γ, η itd.

Jakie może być wzajemne położenie prostej i płaszczyzny w przestrzeni?

Prosta może przecinać płaszczyznę i ma wówczas jeden punkt wspólny (A) z płaszczyzną (np. α).
Wśród prostych przecinających płaszczyznę wyróżniamy proste prostopadłe do płaszczyzny.

Prosta może być równoległa do płaszczyzny. Może nie mieć punktów wspólnych lub (jeśli zawiera się w tej płaszczyźnie) nieskończenie wiele.

Dwie płaszczyzny

Jak mogą być położone w przestrzeni względem siebie dwie płaszczyzny?

1. Dwie płaszczyzny w przestrzeni mogą się przecinać.
Ich wspólne punkty tworzą prostą, która nazywa się krawędzią przecięcia się tych płaszczyzn.

2. Dwie płaszczyzny w przestrzeni mogą być równoległe (nie mają wówczas żadnych punktów wspólnych) lub się pokrywać (mają wówczas nieskończenie wiele punktów wspólnych)..

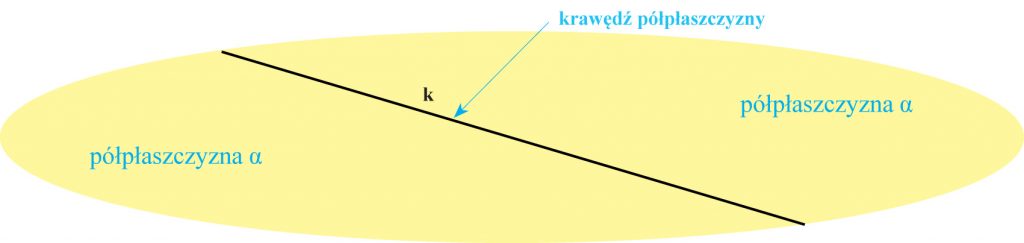
Półpłaszczyzna

Prosta k rozcina płaszczyznę na dwa obszary. Każdy z tych obszarów łącznie z prostą k nazywamy półpłaszczyzną. Prostą k wyznaczającą tę półpłaszczyznę nazywamy krawędzią tej półpłaszczyzny.

Zadanie dla Ciebie!
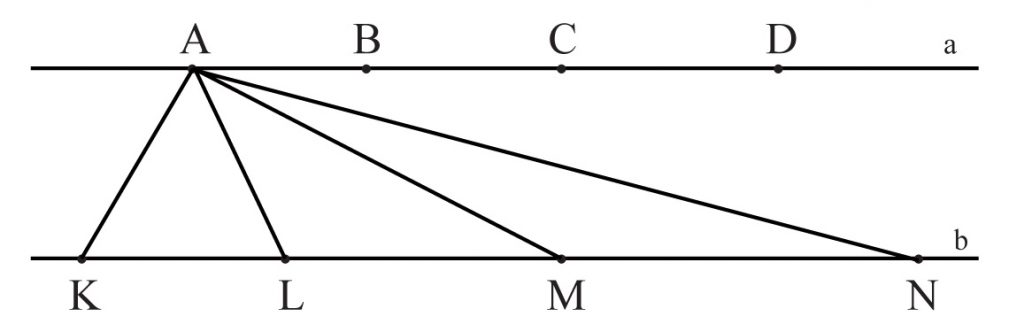
Na każdej z dwóch prostych równoległych obrano po cztery różne punkty. Jaka jest maksymalna liczba trójkątów, których wierzchołkami są te punkty?

Jak to rozwiązać?
Na prostych a i b, takich, że a || b, obieramy po cztery różne punkty.
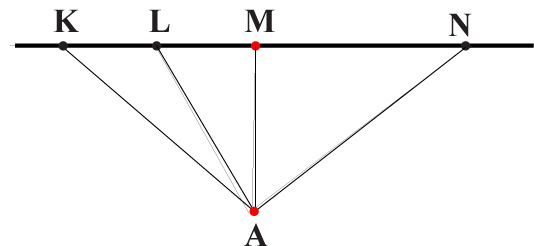
0Można zauważyć, że po połączeniu punktu A należącego do prostej a z punktami K, L, M, N należącymi do prostej b powstaje 6 trójkątów: KLA, KMA, KNA, LMA, LNA, MNA.
Ponieważ mamy 8 różnych punktów, więc po połączeniu każdego z nich z punktami leżącymi na prostej równoległej otrzymamy łącznie 48 trójkątów (6 · 8 = 48).

Sprawdź się!

1. O prostych m, n, k wiadomo, że m || k oraz n || k. Jak położone są względem siebie proste m, n:
A. m n
B. m || n
C. nie można tego ustalić,
D. przecinają się.

2. Dane są 4 niewspółliniowe punkty A, B, C, D. Jeśli przez każde dwa z tych punktów poprowadzimy prostą, to otrzymamy:
A. 2 proste,
B. 3 proste,
C. 4 proste,
D. 6 prostych.

3. Jeżeli punkty K, L, M, N, P, R są współliniowe, to na prostej przechodzącej przez nie leży:
A. nieskończenie wiele punktów,
B. 6 punktów,
C. 7 punktów,
D. 8 punktów.

4. Na płaszczyźnie dane są dwie różne proste m i n. Na prostej m obieramy 3 różne punkty A, B, C, a na prostej n obieramy także 3 różne punkty A1, B1, C1. Przez każde dwa punkty, z których jeden należy do prostej m, a drugi do prostej n, prowadzimy prostą. Ile jest takich prostych?
A. 3
B. 9
C. 6
D. 18

5. W układzie współrzędnych narysuj prostą przechodzącą przez punkty P = (–4, 1) i R = (3, –2). Które z punktów: K = (2, 0), L = (–1, –4), M = (4, 2), N = (0, 4) leżą na tej samej półpłaszczyźnie wyznaczonej przez prostą PR?
A. K, L, M
B. K, L, N
C. K, M, N
D. L, M, N

6. W układzie współrzędnych dane są punkty: A = (–4, –3), B = (3, 4), C = (0, 1), D = (0, –3), E = (3, 0), F = (3, –3), G = (–2, 2). Które z poniżej wymienionych nie są współliniowe?
A. A, B, C
B. A, D, F
C. C, F, G
D. B, E, F

Odpowiedzi: 1. B, 2. D, 3. A, 4. B, 5. C, 6. C