Klasyfikacja i własności trójkątów i czworokątów.
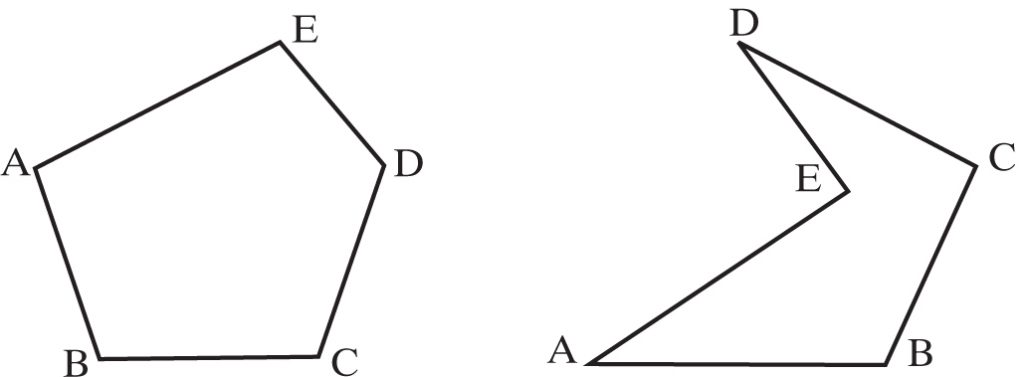
Część płaszczyzny ograniczoną łamaną zwyczajną zamkniętą wziętą razem z tą łamaną nazywamy wielokątem.
Wierzchołki łamanej nazywamy wierzchołkami wielokąta. Boki łamanej nazywamy bokami wielokąta.
Odcinek łączący dwa nie kolejne wierzchołki wielokąta nazywamy przekątną wielokąta.
Ze względu na ilość boków wielokąty dzielimy na:
- Trójkąty – 3 boki
- Czworokąty – 4 boki
- Pięciokąty – 5 boków
- Sześciokąty – 6 boków itd.
Trójkąty
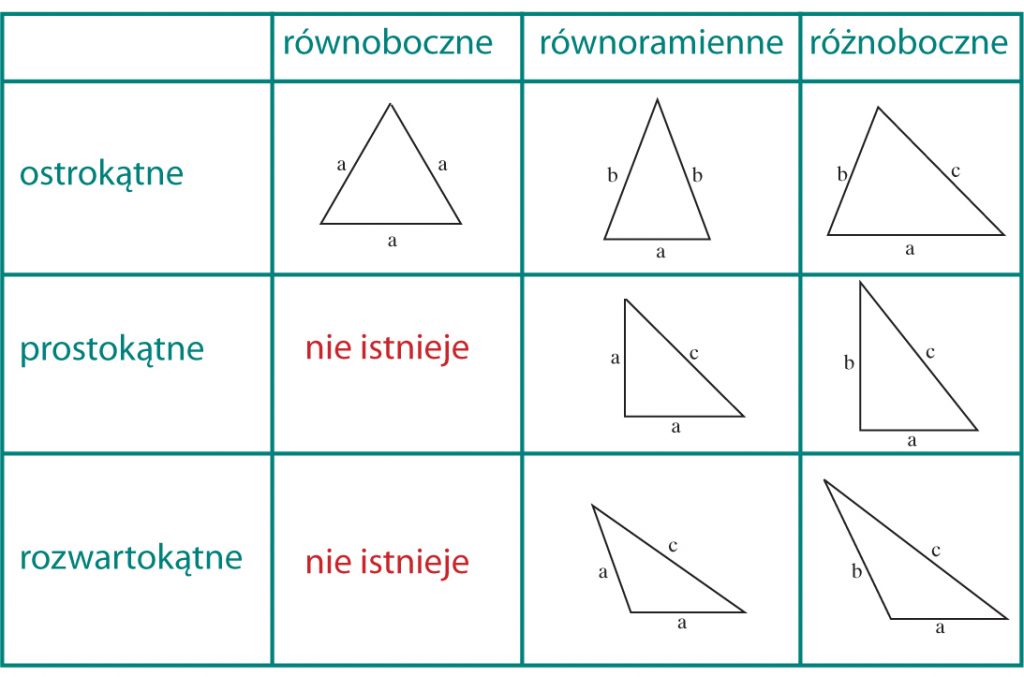
Trójkąty, to wielokąty o najmniejszej liczbie boków. Mogą one być:
- RÓWNOBOCZNE – wszystkie boki jednakowej długości.
- RÓWNORAMIENNE – dwa boki jednakowej długości – zwane ramionami, trzeci inny.
- RÓŻNOBOCZNE – każdy bok innej długości.
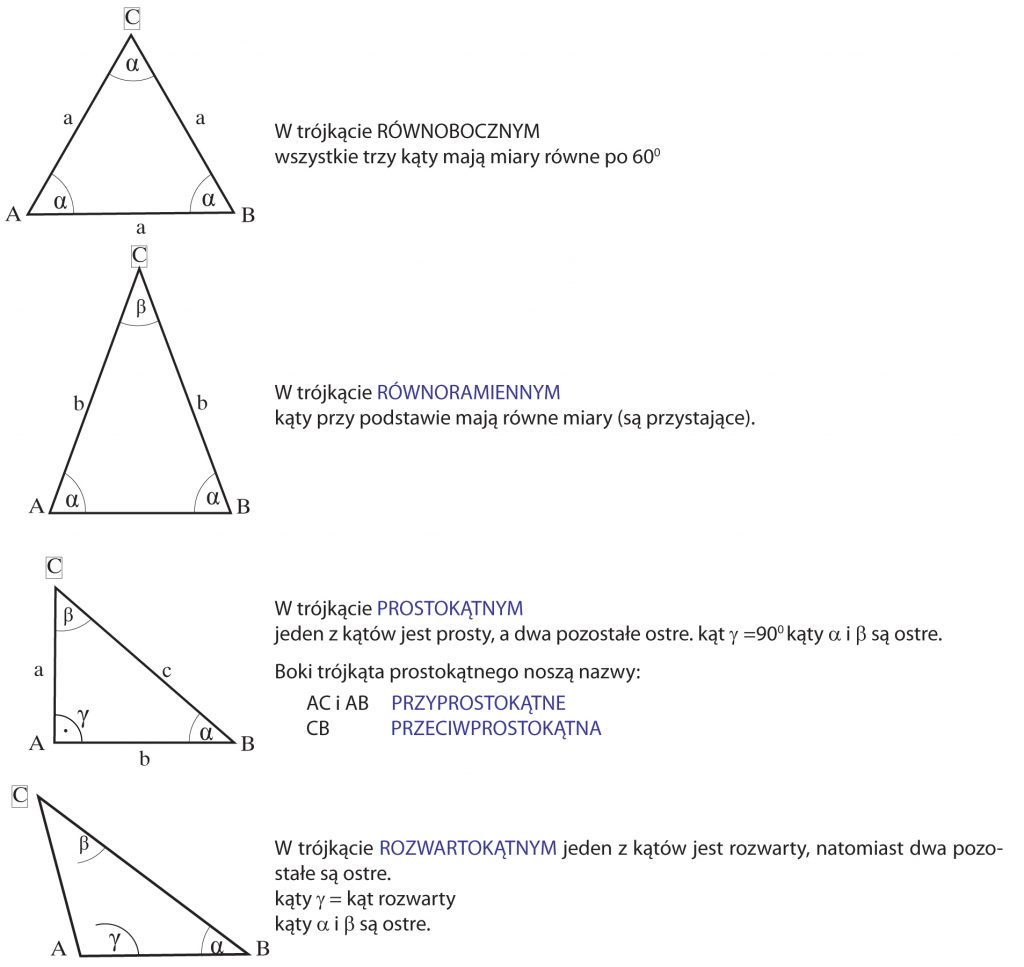
lub - OSTROKĄTNE – wszystkie kąty ostre.
- PROSTOKĄTNE – jeden kąt prosty, dwa kąty ostre.
- ROZWARTOKĄTNE – jeden kąt rozwarty, dwa kąty ostre.
Zadanie 1
Dane są dwie różne miejscowości A i B. Przejdź najkrótszą drogą z miejscowości A do B.
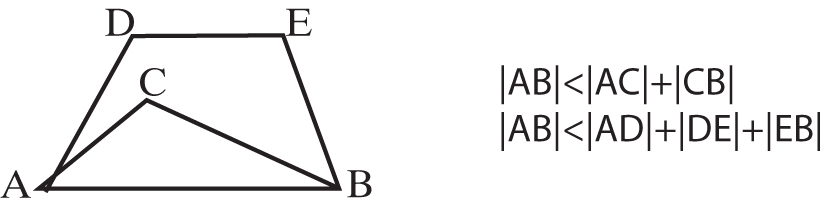
Najkrótsza droga to długość odcinka AB. Długość każdej łamanej łączącej punkty A i B jest większa niż długość odcinka AB.
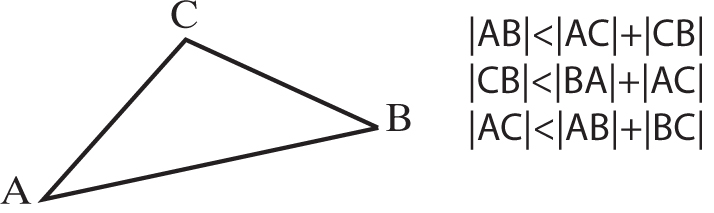
Podobnie jest w każdym trójkącie:
Każdy bok trójkąta jest mniejszy od sumy dwóch pozostałych boków.
Zadanie 2
Czy odcinki o podanych długościach mogą być bokami trójkąta.
1)
a = 9 cm, b = 8 cm, c = 7 cm
Sprawdzamy:
9 + 8 > 7
9 + 7 > 8
8 + 7 > 9
Tak, gdyż suma długości każdych dwóch odcinków jest większa od długości trzeciego.
2)
a = 9 cm, b = 2 cm, c = 4 cm.
9 + 2 > 4
9 + 4 > 2
4 + 2 < 9
Nie, gdyż suma odcinków b+c jest mniejsza a nie większa od długości odcinka a.
Zastanówmy się ile wynosi suma kątów wewnętrznych każdego trójkąta.
Zastanówmy się ile wynosi suma kątów wewnętrznych każdego trójkąta.
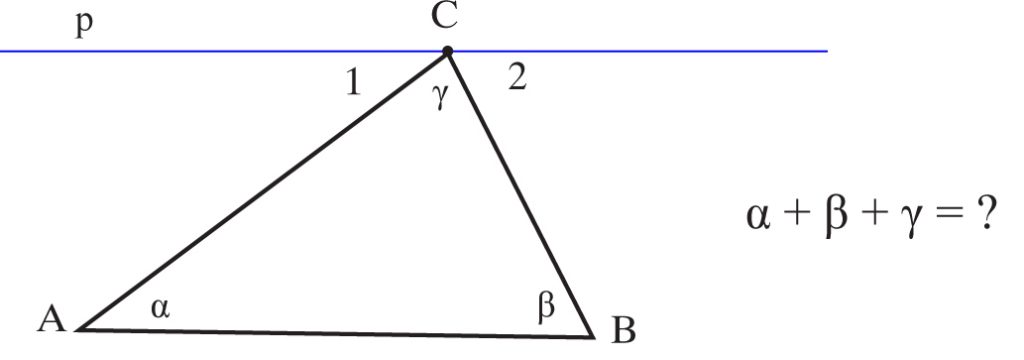
Poprowadźmy przez wierzchołek C prostą p równoległą do boku AB. Zauważmy, że:
kąt 1 = kąt α
kąt 2 = kąt β
kąt 1 + kąt γ + kąt 2 = 180° (kąt półpełny). Podstawiając zamiennie otrzymujemy kąt a + kąt γ + kąt b = 180° tzn.:
SUMA MIAR KĄTÓW WEWNĘTRZNYCH TRÓJKĄTA WYNOSI 180°.
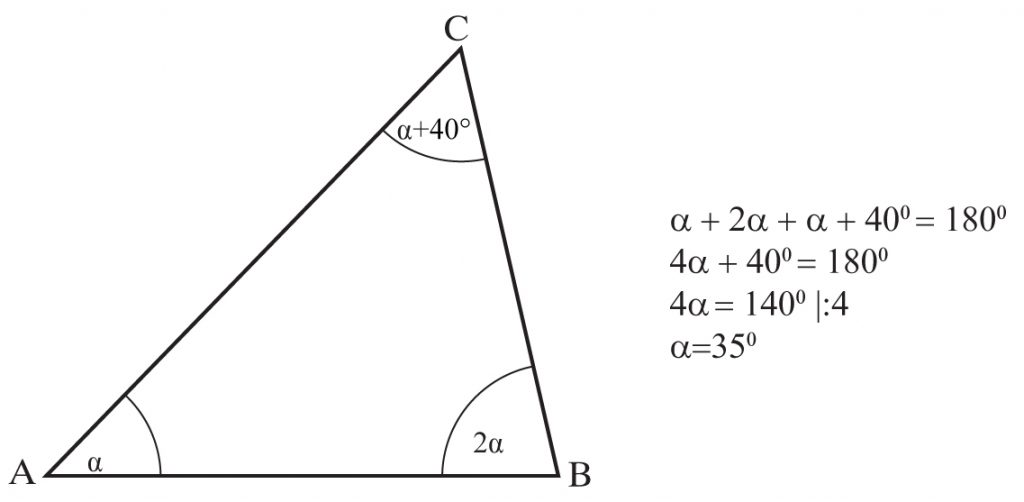
Zadanie 3
Oblicz miarę kąta α.
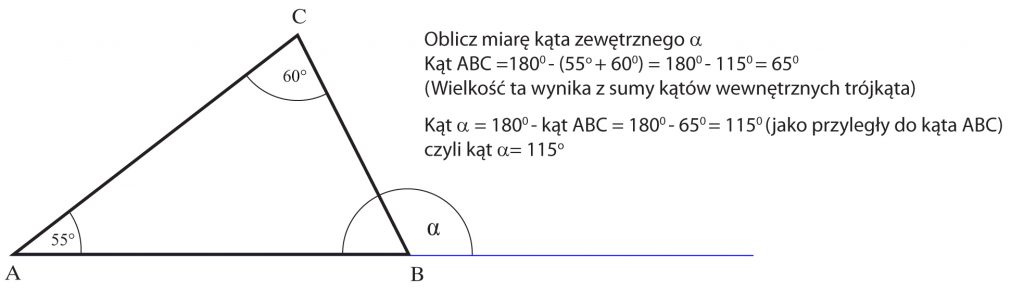
Kąt przyległy do kąta wewnętrznego trójkąta nazywa się kątem ZEWNĘTRZNYM tego trójkąta.
Pamiętaj!
Kąt zewnętrzny trójkąta równy jest sumie dwóch kątów wewnętrznych do niego nie przyległych.
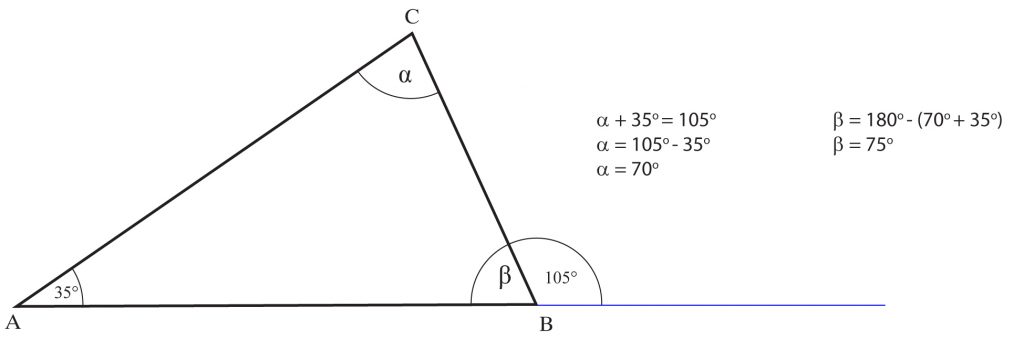
Zadanie 4
Przypatrz się rysunkowi i podaj miary kątów α i β.
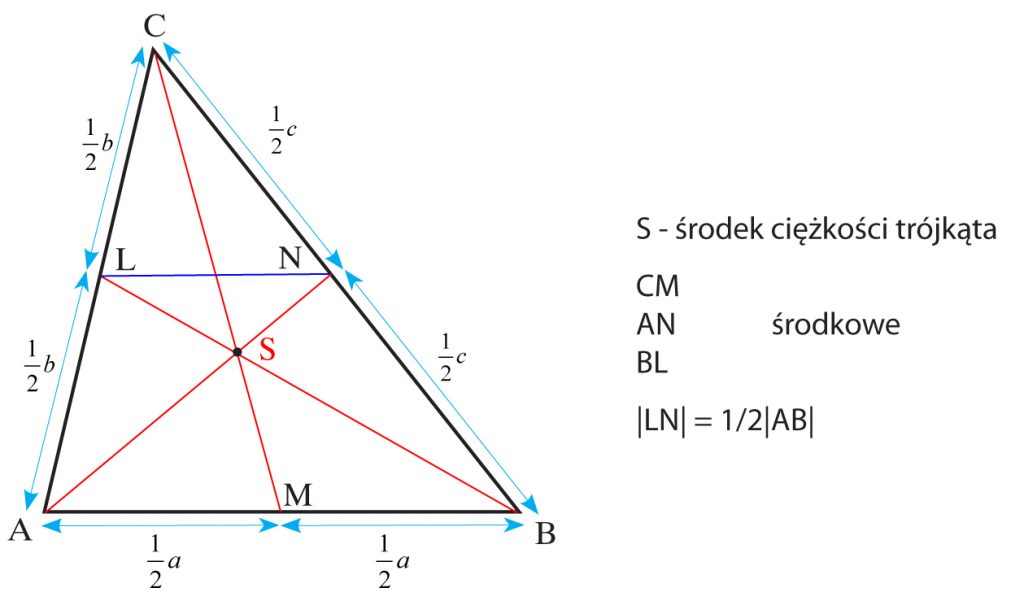
ŚRODKOWĄ TRÓJKĄTA nazywamy odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
Każdy trójkąt posiada trzy środkowe, które przecinają się w jednym punkcie zwanym ŚRODKIEM CIĘŻKOŚCI trójkąta.
Zapamiętaj!
Odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i równy jego połowie.
Punkt przecięcia środkowych dzieli każdą ze środkowych w stosunku 2:1 licząc od wierzchołka, tzn.
|SM| = 1/3 |CM| a |CS| = 2/3|CM| czyli |SM|=1/2|CS|
Ważnym pojęciem w geometrii jest ODLEGŁOŚĆ.
Zadanie 5
Znajdź odległość punktu A, nie leżącego na prostej p, od tej prostej.
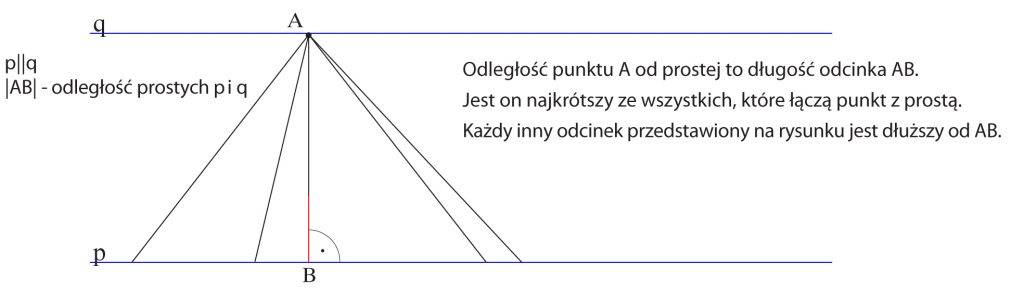
Zapamiętaj!
Odległością punktu od prostej nazywamy długość odcinka łączącego punkt z prostą i prostopadłego do tej prostej.
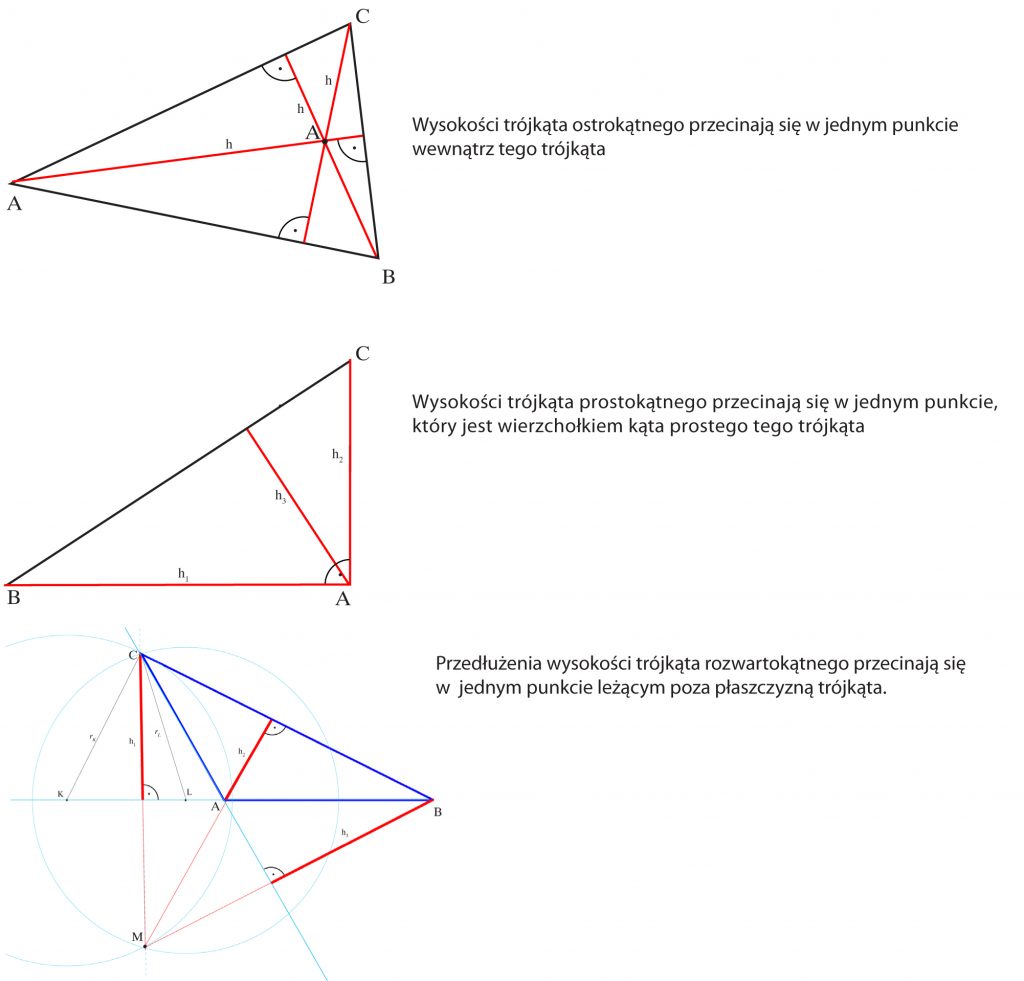
W trójkącie – ODLEGŁOŚĆ wierzchołka od przeciwległego boku nazywamy WYSOKOŚCIĄ tego trójkąta. Każdy trójkąt ma trzy wysokości.
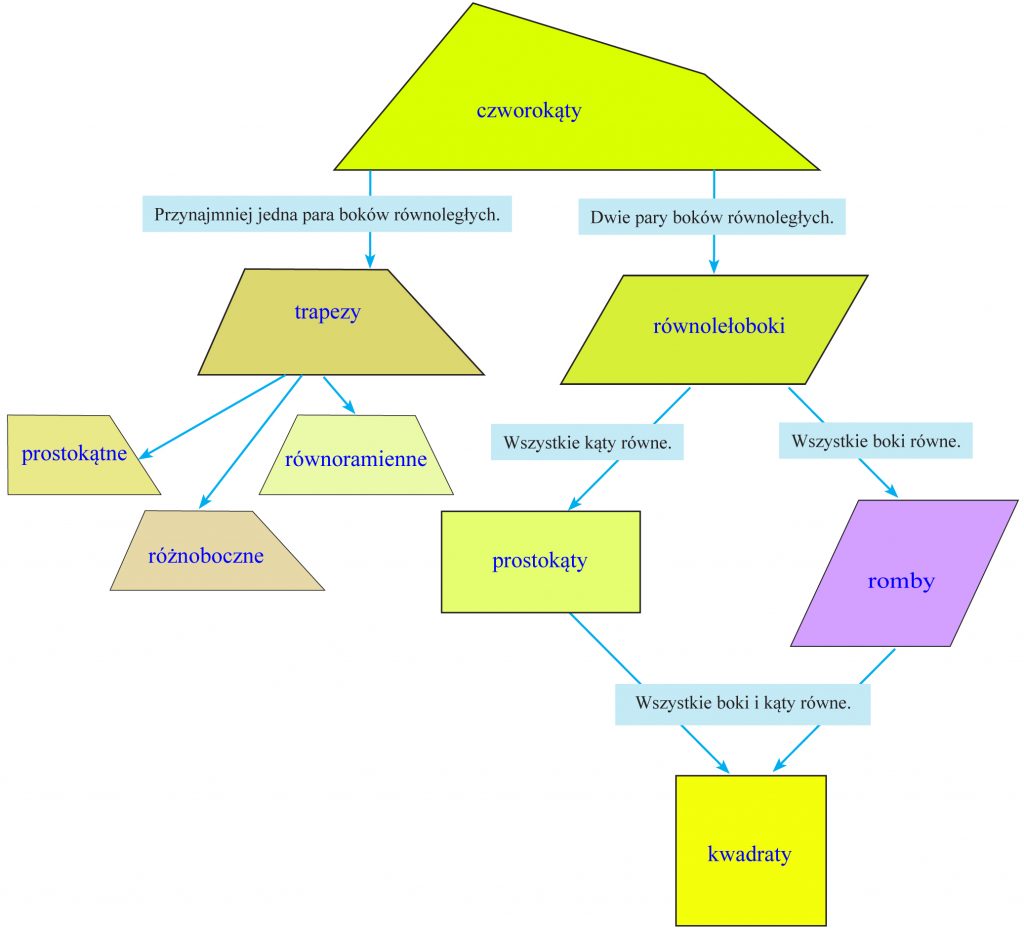
CZWOROKĄTY
Czworokąty, to wielokąty mające 4 boki. A oto ich klasyfikacja (podział).
Niektóre źródła matematyczne podają inny podział, w którym równoległoboki są trapezami. Nie ma to większego znaczenia, gdyż nie wpływa to na własności wymienionych czworokątów.
Własności poszczególnych czworokątów
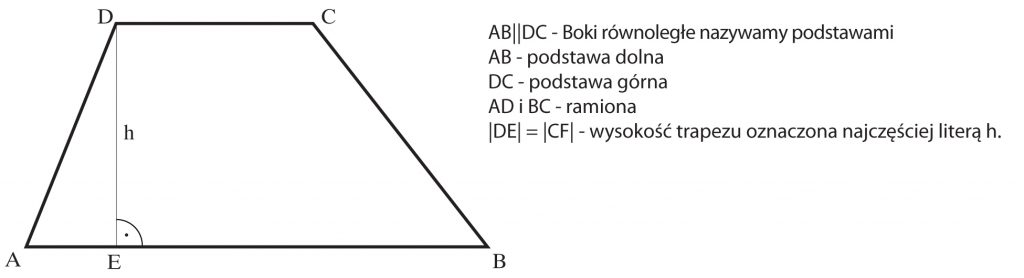
TRAPEZ to czworokąt mający jedną parę boków równoległych.
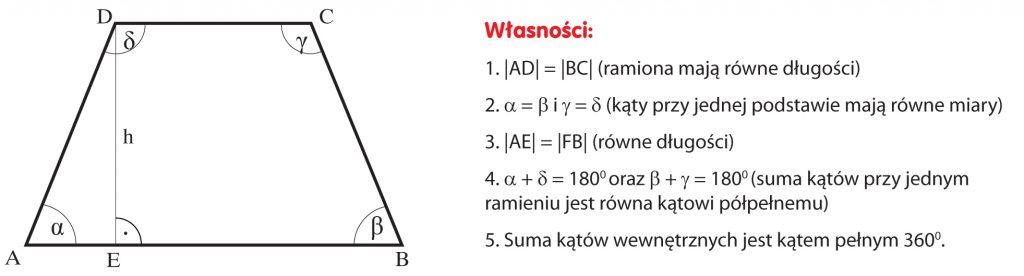
Powyższy trapez nazywa się różnobocznym, gdyż jego boki mają różne długości. Jeśli ramiona trapezu są równe, trapez nazywamy RÓWNORAMIENNYM.
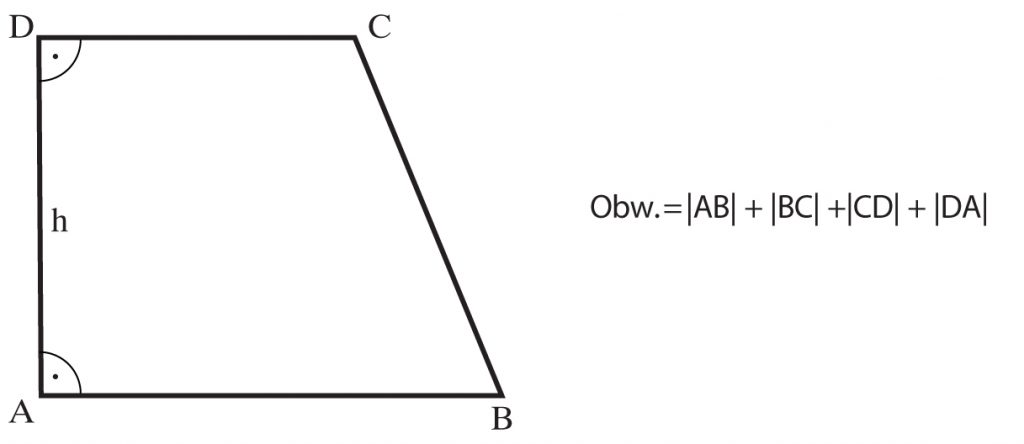
Trapez posiadający dwa kąty proste nazywa się PROSTOKĄTNYM.
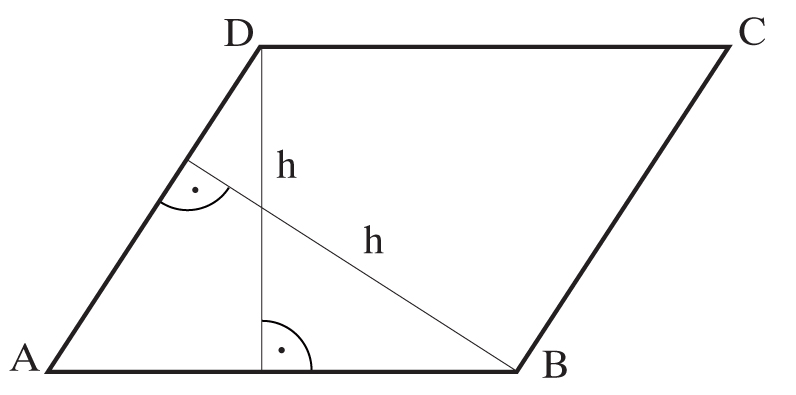
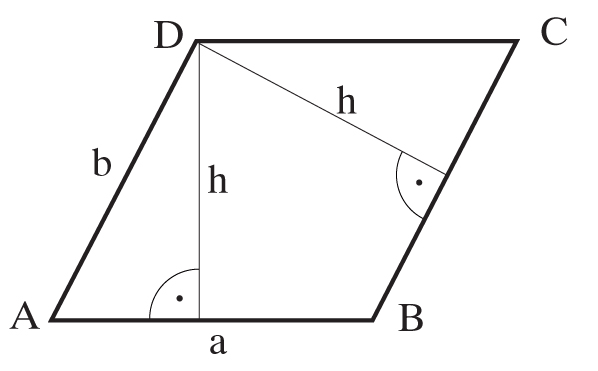
RÓWNOLEGŁOBOK, to czworokąt posiadający dwie pary boków równoległych.
RÓWNOLEGŁOBOK ma dwie różne wysokości.
PROSTOKĄT to równoległobok posiadający kąty proste.
Własności:
1. AD || BC oraz AB || DC (boki przeciwległe są równoległe)
2. |AD| = |BC| oraz |AB| = |DC| (boki przeciwległe są równej długości)
3. kąt A = kąt C = kąt B = kąt D = 90o (każdy kąt wewnętrzny jest kątem prostym)
4. kąt A + kąt B = 180o (suma kątów leżących przy jednym boku ma miarę 180o)
5. kąt A + kąt B + kąt C + kąt D = 360o (suma wszystkich kątów wewnętrznych ma miarę 360o)
6. |AO| = |OC| oraz |DO| = |OB| (przekątne dzielą się na połowy)
7. |AC| = |DB| przekątne mają równe długości.
ROMB to równoległobok o równych bokach.
Własności:
1. AD || CB oraz AB || DC
2. |AD| = |CB| = |AB| = |DC|
3. kąt A = kąt C oraz kąt B = kąt D
4. kąt A + kąt B = 180°
5. kąt A + kąt B + kąt C + kąt D = 360°
6. |AO| = |OC| oraz |DO| = |OB|
7. przekątne dzielą kąty rombu na połowy
8. AC ⊥ BD (przekątne są prostopadle)
ROMB ma jedną wysokość.
Obie wysokości mają taką samą długość. Obwód = 4a (obwód to suma długości wszystkich boków)
KWADRAT to prostokąt o równych bokach lub KWADRAT to romb o prostych kątach.
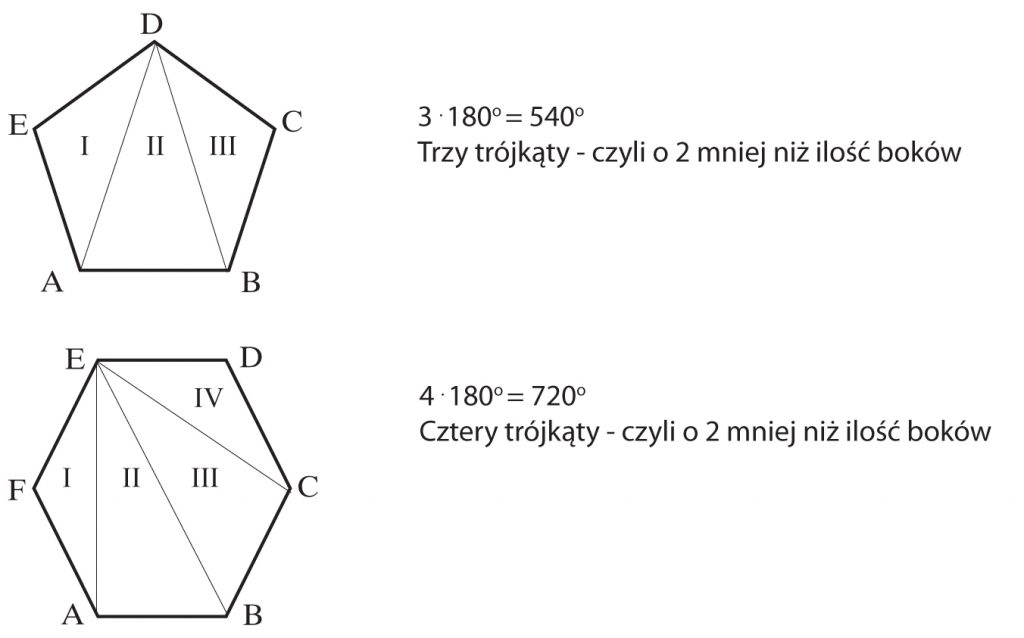
Mówiliśmy dotychczas, o sumie kątów wewnętrznych trójkąta i czworokąta. A jak jest z pięciokątem, sześciokątem itp. Wielokątem wypukłym. Zadanie jest proste. Dzielimy wielokąt wypukły na trójkąty. Suma kątów wewnętrznych wielokąta wypukłego = ilość trójkątów . 180°
A zatem:
Suma kątów wewnętrznych wielokąta wypukłego = ilość trójkątów . 180° = (n-2) . 180°
gdzie n oznacza liczbę boków wielokąta.