TRÓJKĄTY

POWTARZAMY TRÓJKĄTY

Wielokątem o najmniejszej liczbie boków jest trójkąt.

• Trójkąt to część płaszczyzny ograniczona łamaną zwyczajną zamkniętą złożoną z 3 odcinków.
• Trójkąt ma trzy wierzchołki i trzy kąty wewnętrzne.

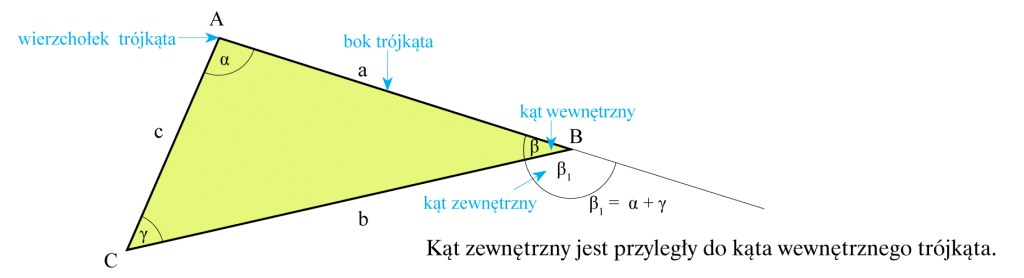
A, B, C – wierzchołki trójkąta
AB, AC, BC – boki trójkąta
ABC, ACB, CAB – kąty wewnętrzne trójkąta

Zapamiętaj!

• Wierzchołki trójkąta oznaczamy dużymi literami A, B, C.
• Boki trójkąta oznaczamy małymi litrami a, b, c.
• Kąty oznaczamy greckimi literami α (przy wierzchołku A) , β, (przy wierzchołku B), γ (przy wierzchołku C) itd.
• Każdy bok trójkąta ma długość mniejszą od sumy długości dwóch pozostałych boków.
  a < b + c
  b < a + c
  c < a + b
• Naprzeciwko najmniejszego kąta leży bok najkrótszy, naprzeciwko największego kąta – bok najdłuższy.
• Kąt przyległy do kąta wewnętrznego trójkąta nazywamy kątem zewnętrznym trójkąta.
• Kąt zewnętrzny trójkąta jest równy sumie dwóch kątów wewnętrznych do niego nieprzyległych.
• Suma kątów wewnętrznych trójkąta wynosi 180°.

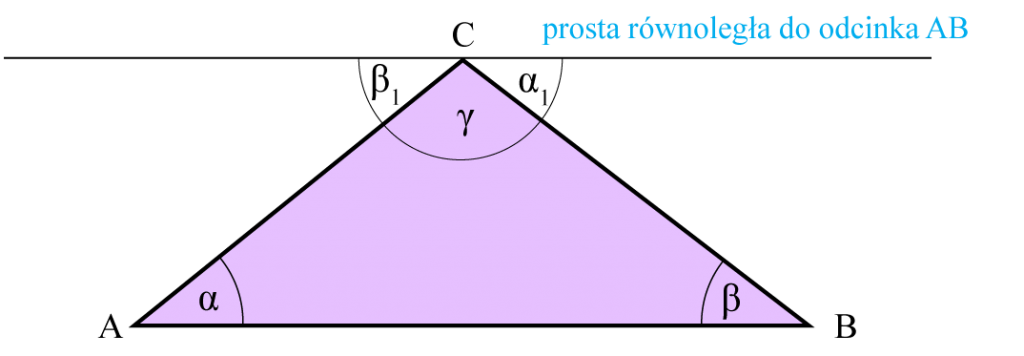
Dowód:
Jeśli w trójkącie ABC poprowadzimy prostą równoległą do AB przechodzącą przez wierzchołek C, to otrzymamy kąt naprzemianległe do kątów α i β – katy α₁ i β₁.

Jak widać kąty α₁, γ, β₁ stanowią razem kąt półpełny 180°.

 

Pole trójkąta

Pole trójkąta obliczamy mnożąc jego podstawę przez wysokość opuszczoną do tej podstawy i dzieląc przez 2.

Obwód trójkąta

Obwód trójkąta jest sumą długości poszczególnych boków a+b+c.

 

Podział trójkątów

Ze względu na boki

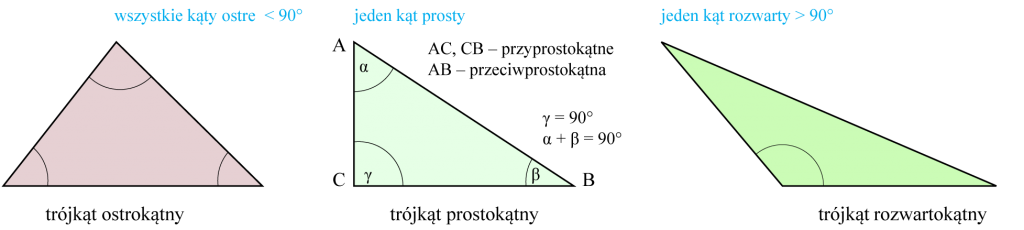
Ze względu na kąty

Zapamiętaj definicje!
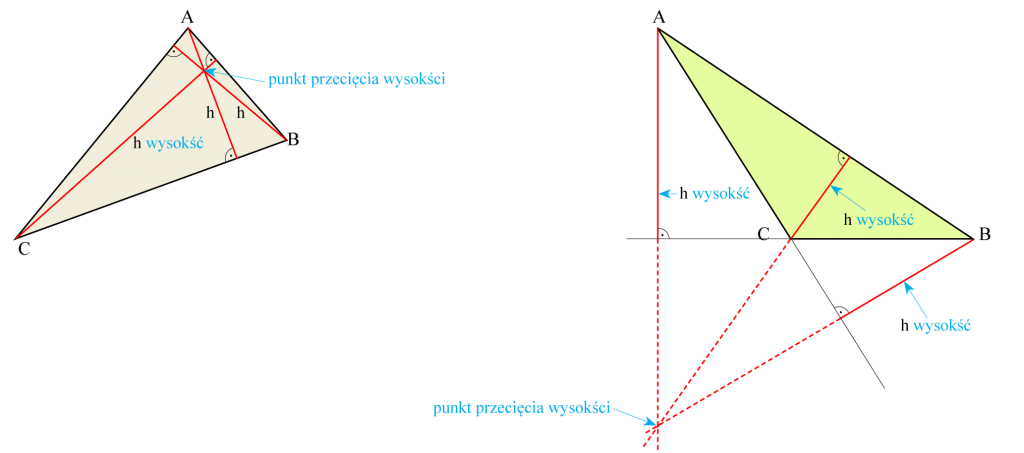
Wysokość trójkąta jest to prostopadły odcinek poprowadzony z danego wierzchołka do boku (lub jego przedłużenia) leżącego naprzeciwko.

• Każdy trójkąt ma trzy wysokości.
• Wysokości trójkąta przecinają się w jednym punkcie.
• Punkt przecięcia wysokości może leżeć poza trójkątem.

 

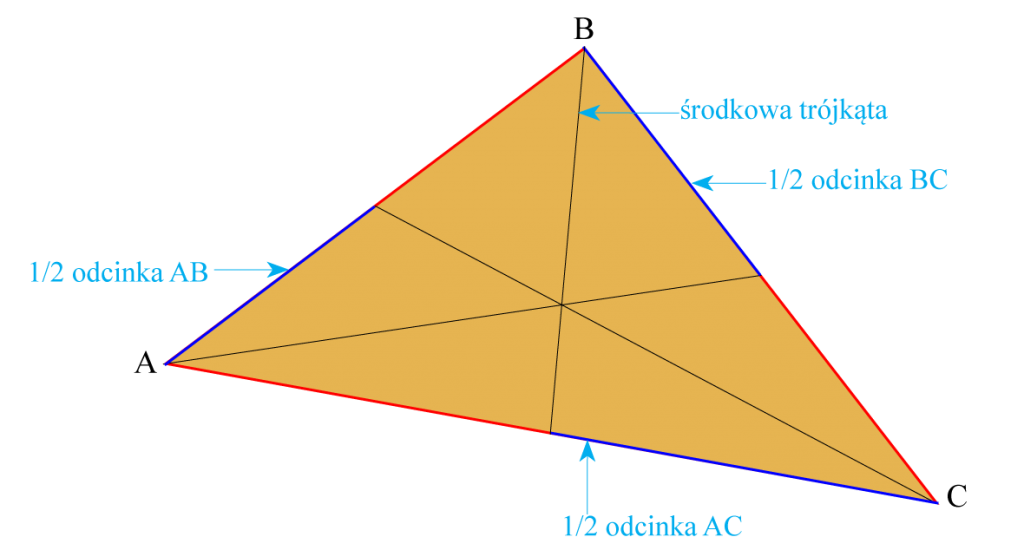
Środkowa trójkąta – odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.

• Trójkąt ma trzy środkowe, które przecinają się w jednym punkcie.
• Punkt przecięcia trzech środkowych trójkąta nazywa się środkiem ciężkości trójkąta.

Dwusieczne kątów trójkąta – półproste dzielące kąty na połowy. Ich punkt przecięcia jest środkiem okręgu wpisanego w trójkąt.

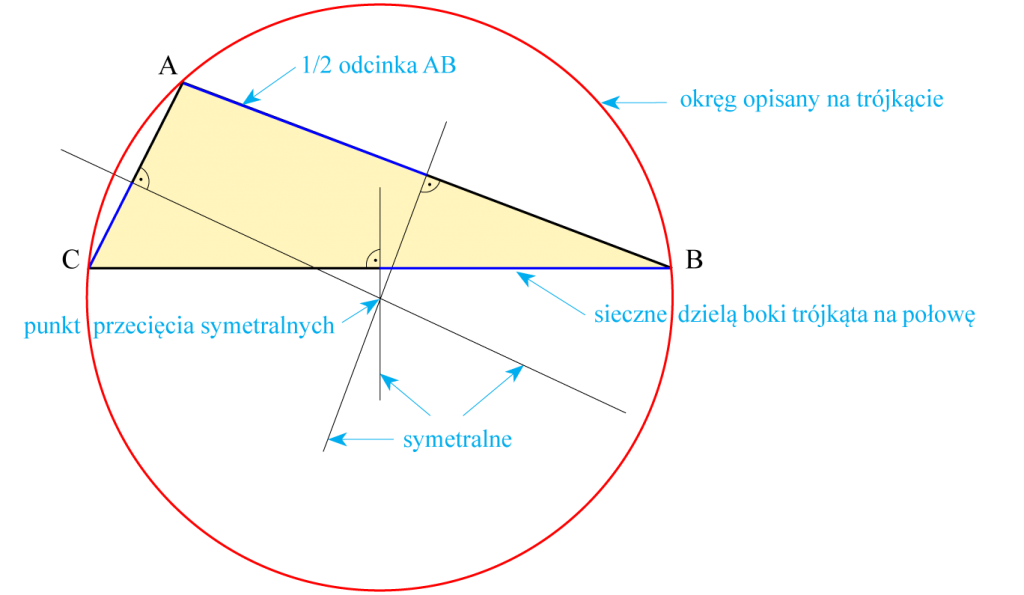
Symetralne boków trójkąta są to proste prostopadłe do boków i dzielące je na połowy.

 

• Punkt przecięcia symetralnych jest środkiem okręgu opisanego na trójkącie.
• Symetralne mogą przecinać się poza trójkątem.
• W trójkącie równobocznym symetralne boków zawierają dwusieczne kątów, środkowe i wysokości.
• W trójkącie prostokątnym symetralne przecinają się w punkcie, który jest środkiem przeciwprostokątnej.

 

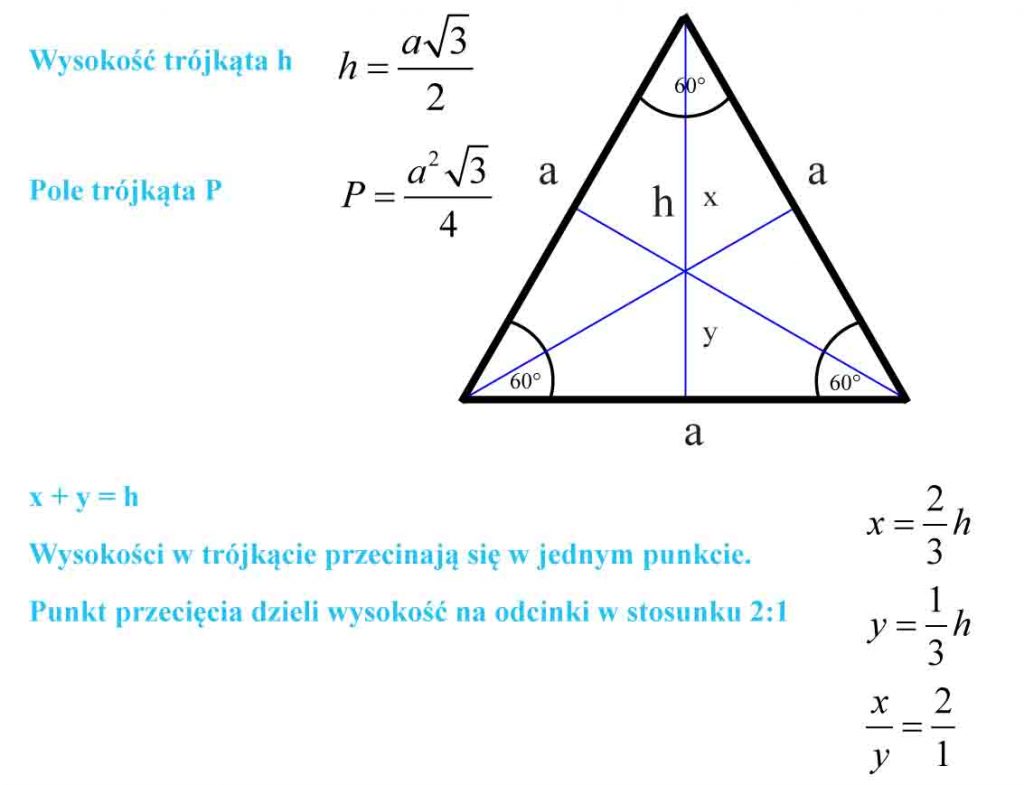
Trójkąt równoboczny

Trójkąt równoboczny – trójkąt, którego wszystkie boki mają taką samą długość. Jest przykładem wielokąta foremnego.

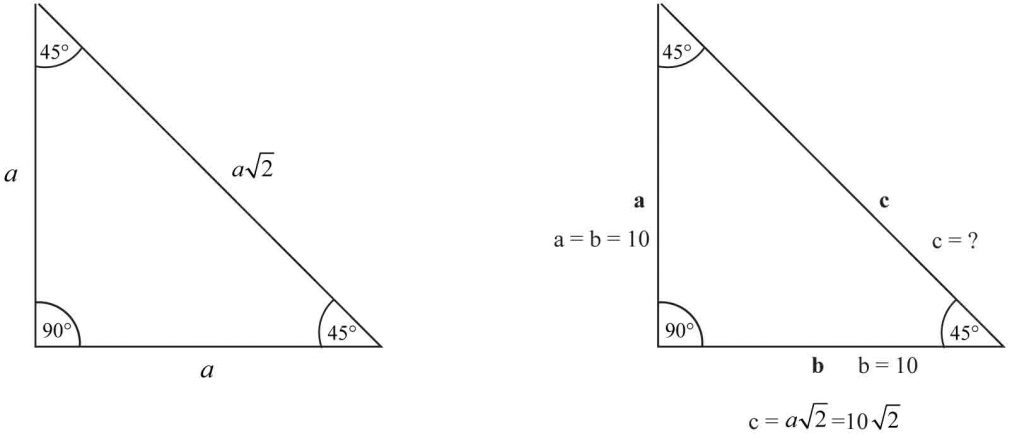
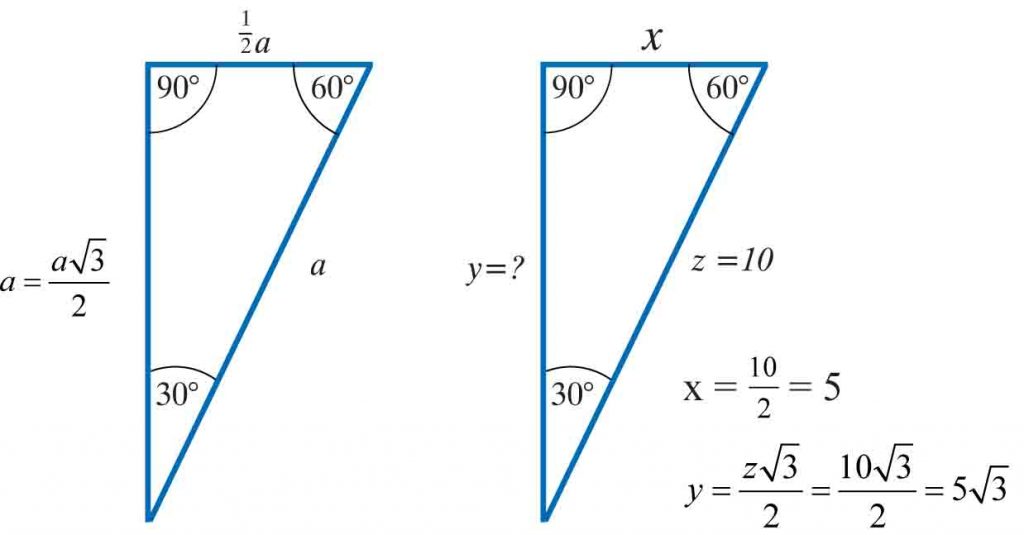
Wyorz na długość boków trójkąta prostokątnego

o kątach 45°, 90°, 45°

o kątach 30°, 90°, 60°

Zadania

Zadanie 1.
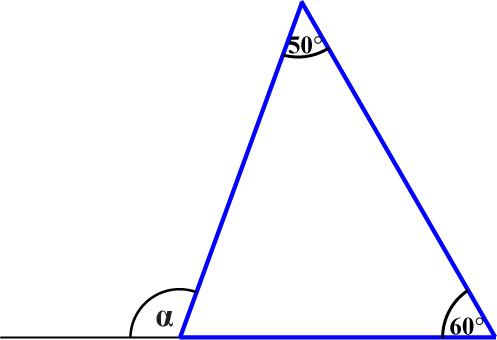
Oblicz miarę kąta α.

Odpowiedź
Ponieważ suma kątów w trójkącie wynosi 180°, zatem trzeci kąt trójkąta ma 70°. Kąt ten i kąt α są kątami przyległymi, czyli miara nieznanego kąta wynosi 110°.
Zauważ, że 50° + 60° = 110°, a kąt ma właśnie 110°.

Zadanie 2.
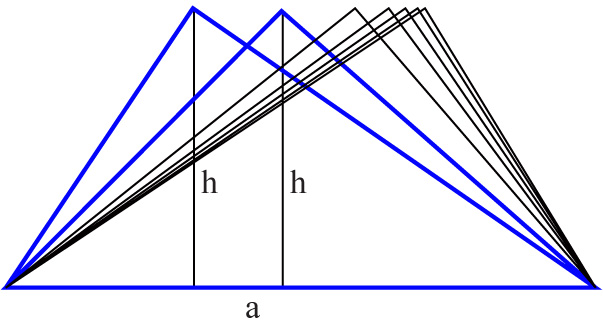
Narysuj trójkąt, w którym podstawa ma długość a, a wysokość opuszczona na tą podstawę długość h. Ile takich trójkątów można narysować?

Zrób rysunek pomocniczy!

Odpowiedź
Takich trójkątów jest nieskończenie wiele.
Z każdego punktu podstawy można poprowadzić odcinek o długości h, który jest prostopadły do tej podstawy.

Poćwicz do testu!

1. Dane są miary dwóch kątów trójkąta. Który z tych trójkątów jest równoramienny:
A. 50°, 100°
B. 15°, 150°
C. 50°, 60°
D. 60°, 70°

2. Jeżeli dwa boki trójkąta mają długości 2 m i 60 dm, to trzeci bok może mieć długość:
A. 80 dm
B. 20 dm
C. 4 m
D. 6 m

3. W trójkącie rozwartokątnym wysokości lub ich przedłużenia przecinają się:
A. wewnątrz trójkąta,
B. w wierzchołku trójkąta,
C. na zewnątrz trójkąta,
D. nie można określić.

4. Pan Nowak ma działkę w kształcie trójkąta prostokątnego. Wejście na tę działkę znajduje się na środku przeciwprostokątnej. Właściciel postanowił, że od wejścia do altany znajdującej się w wierzchołku kąta prostego poprowadzi wzdłuż prostej ścieżkę. Wytyczona ścieżka jest:
A. wysokością trójkąta,
B. symetralną przeciwprostokątnej,
C. środkową trójkąta,
D. dwusieczną kąta prostego.

Odpowiedzi:
1. B, 2. D, 3. C, 4. C.