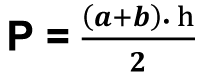Czworokąt jest to część płaszczyzny ograniczona łamaną zwyczajną zamkniętą złożoną z 4 odcinków.
- Ma cztery wierzchołki i cztery kąty wewnętrzne, których suma wynosi 360°. Łatwo można sprawdzić, że suma miar kątów wewnętrznych czworokąta wynosi 360°.
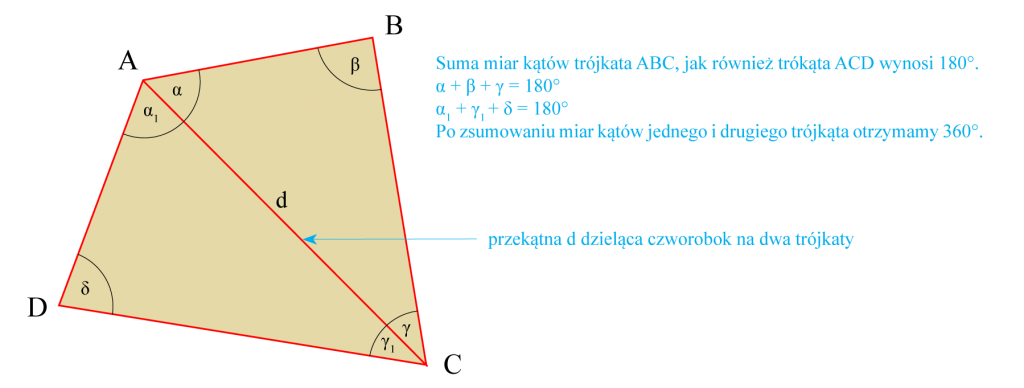
- Jeżeli w dowolnym czworokącie poprowadzisz jedną przekątną, to czworokąt zostanie podzielony na dwa trójkąty. Ponieważ suma miar kątów jednego trójkąta wynosi 180°, więc w obu jest ona równa 360°.
- Wierzchołki czworokąta oznaczamy dużymi literami alfabetu A, B, C, D.
- Przekątna wielokąta to odcinek łączący dwa niekolejne (przeciwległe) wierzchołki wielokąta. W każdym czworokącie można poprowadzić dwie przekątne. Przekątne oznaczamy zazwyczaj literą d.
Czworokąty i ich własności
Trapezoid (na rysunku powyżej) jest najmniej regularnym z czworoboków, ponieważ nie ma on boków równoległych, jak w pozostałych czworokątach. Jego pole powierzchni obliczamy sumując pola powierzchni trójkątów uzyskanych przez podzielenie figury przekątną.
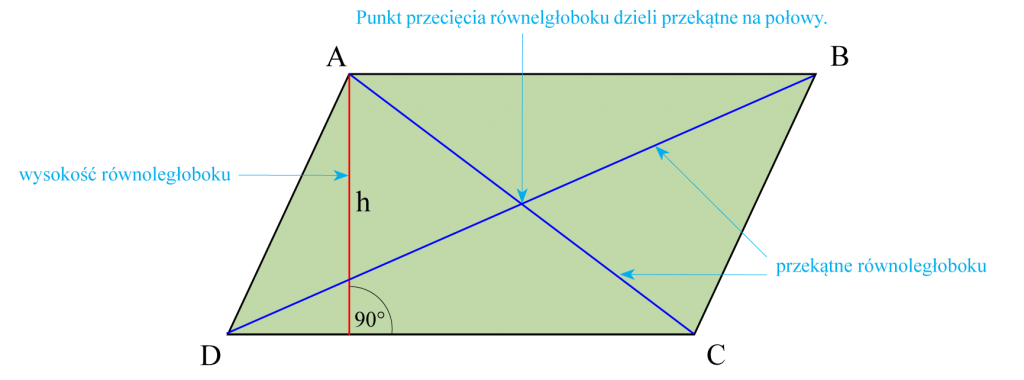
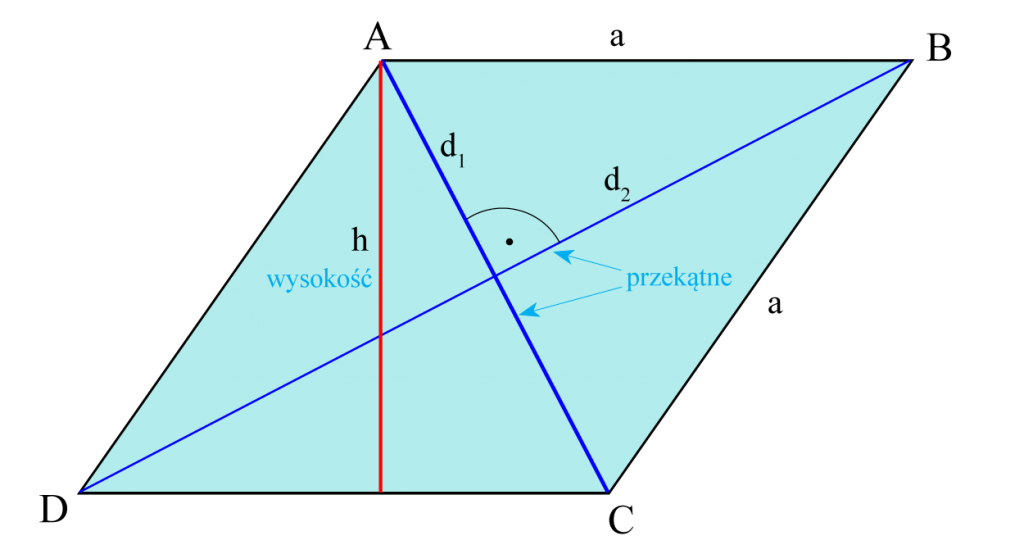
Równoległobok
- ma dwie pary boków równych i równoległych,
- punkt przecięcia przekątnych dzieli je na połowy,
- przeciwległe kąty są równej miary,
- suma kątów leżących przy tym samym boku wynosi 180º.
- Pole powierzchni obliczamy mnożąc podstawę i wysokość.
P = a • h - Obwód obliczamy dodając długości jego boków
Ob = 2a + 2b
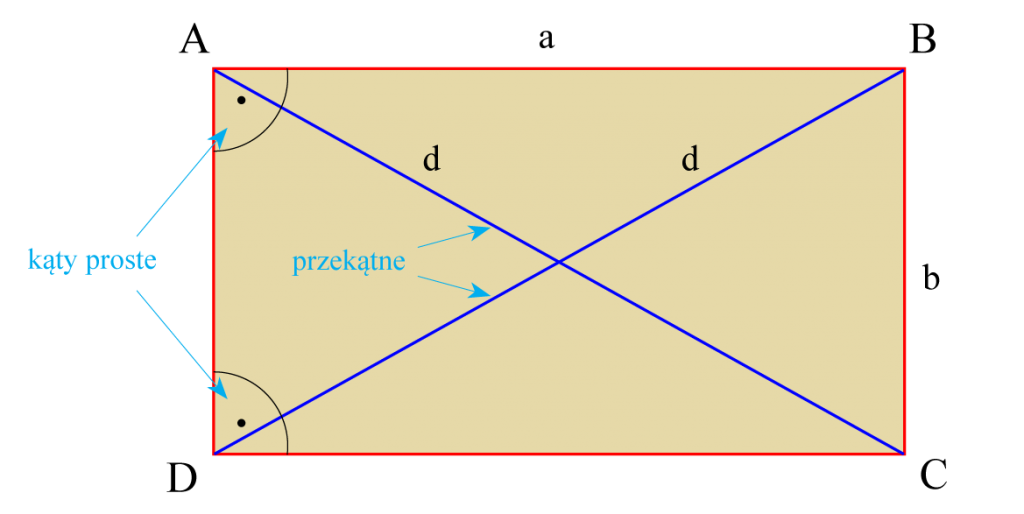
Prostokąt
- jest równoległobokiem, któryo ma wszystkie kąty proste,
- jego przekątne są równej długości i dzielą się na połowy.
- Pole powierzchni obliczamy mnożąc podstawę i wysokość.
P = a • h
- Obwód prostokąta obliczamy dodając kolejno jego boki.
Ob = 2a + 2b
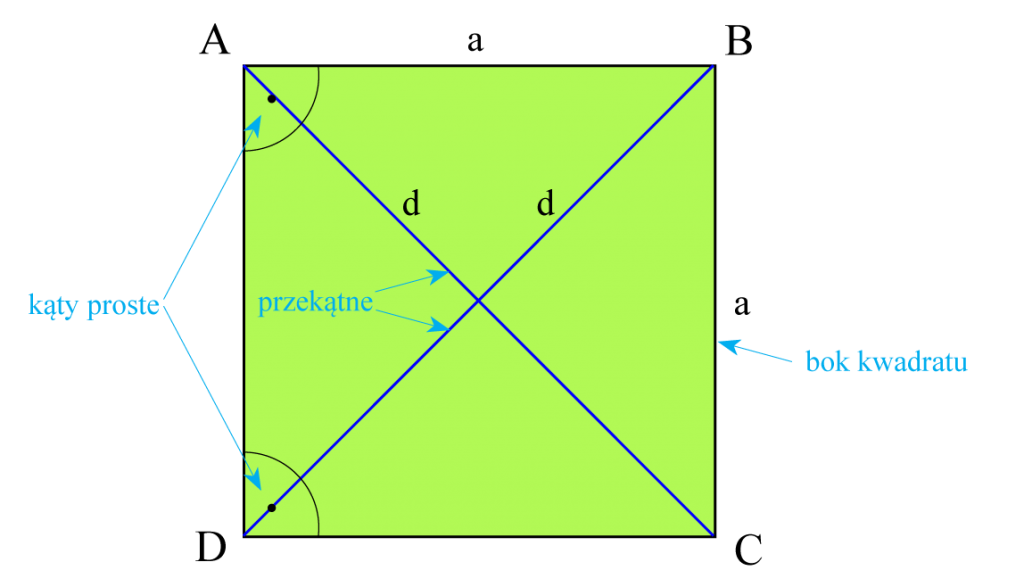
Kwadrat
- jest prostokątem, który ma wszystkie boki równe;
- ma wszystkie kąty proste;
- jego przekątne są:
- równej długości,
- prostopadłe,
- dwusiecznymi kątów wewnętrznych,
- osiami symetrii oraz dzielą się na połowy.
- Pole powierzchni
- Obwód
Ob = 4a
Romb
- jest równoległobokiem, który ma wszystkie boki równe;
- przekątne d1, d2 są:
- prostopadłe,
- dwusiecznymi kątów wewnętrznych,
- osiami symetrii,
- dzielą się na połowy.
Uwaga! Szczególnym przypadkiem rombu (o wszystkich kątach prostych) jest kwadrat.
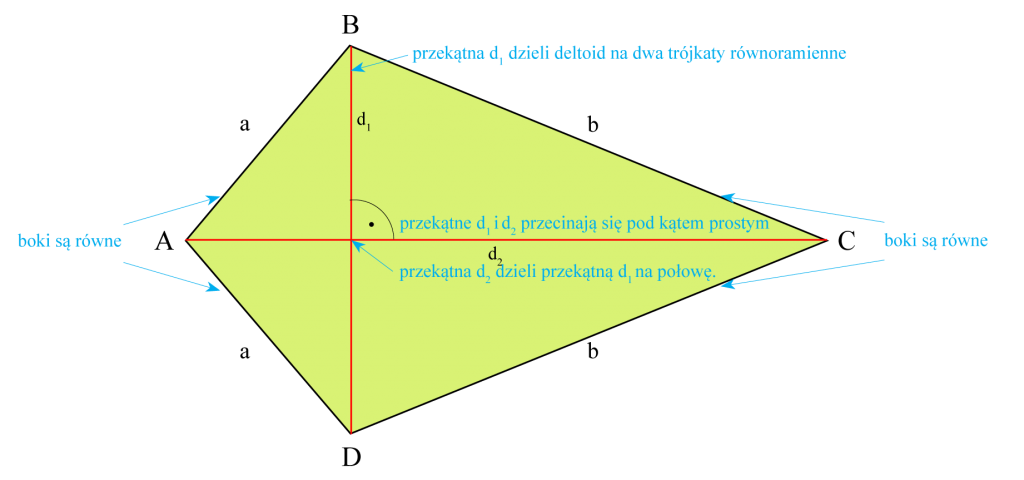
Deltoid
Deltoidem jest to czworokąt mający dwie pary boków sąsiednich równych i w którym żadne dwa boki nie są wzajemnie równoległe.
- dwie pary boków są równe;
- przekątne są prostopadłe;
- jedna z przekątnych dzieli drugą na połowę
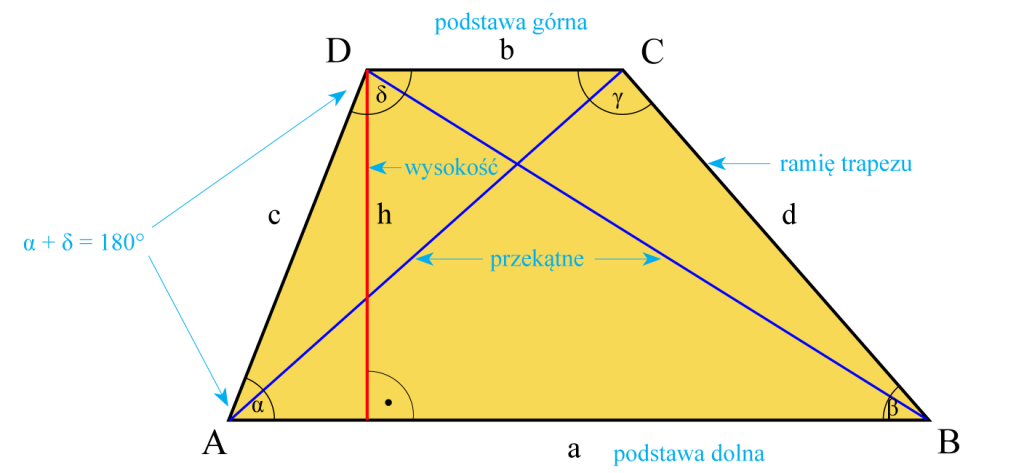
Trapez
- jest czworokątem, który ma dwa boki równoległe, które nazywamy podstawami trapezu,
- odcinek łączący obie podstawy pod kątem prostym nazywamy wysokością,
- Trapez różnoramienny:
- ma wszystkie boki różnej długości;
- kąty wewnętrzne są różnej miary;
- ma dwa kąty ostre i dwa rozwarte.
- Suma miar kątów leżących przy tym samym ramieniu trapezu jest równa 180°.
α + δ = 180°,
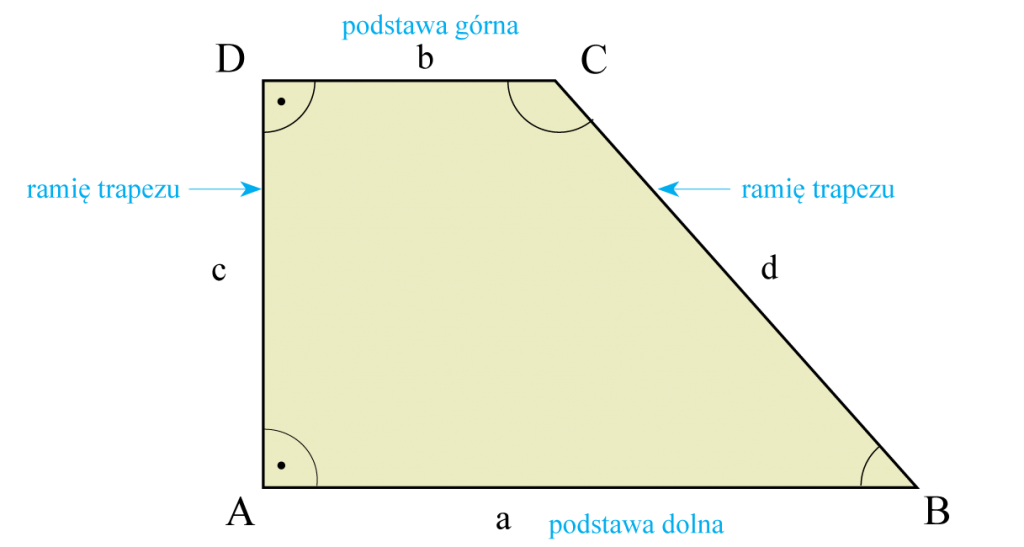
β + γ = 180°. - W trapezie prostokątnym jedno ramię tworzy z podstawami kąty proste.
- Ramię to jest równocześnie wysokością trapezu prostokątnego.
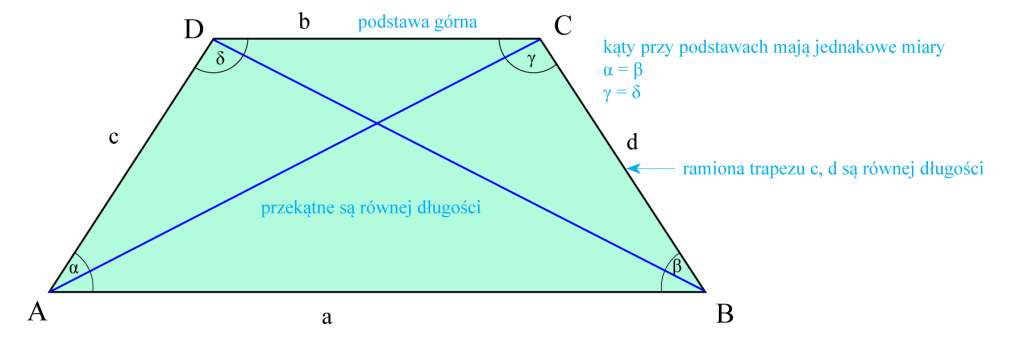
- W trapezie równoramiennym
- dwa boki są równoległe,
- ramiona są równe,
- kąty przy podstawach mają równe miary,
- przekątne są równej długości
- Wzór na pole powierzchni trapezu
- Obwód trapezu obliczamy dodając po kolei jego boki
Ob = a + b + c + d
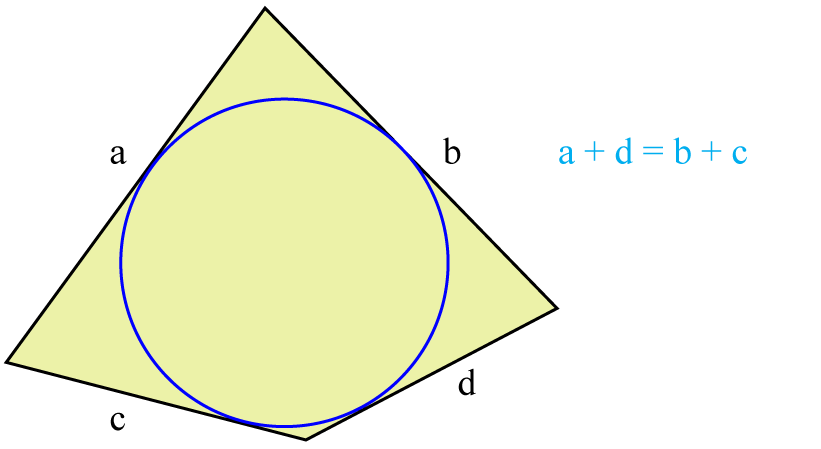
Uwaga 1
Jeśli sumy długości przeciwległych boków czworokąta wypukłego są równe, to można w ten czworokąt wpisać okrąg.
Uwaga 2
Jeżeli suma miar przeciwległych kątów wewnętrznych danego czworokąta wypukłego wynosi 180°, to można na nim opisać okrąg.
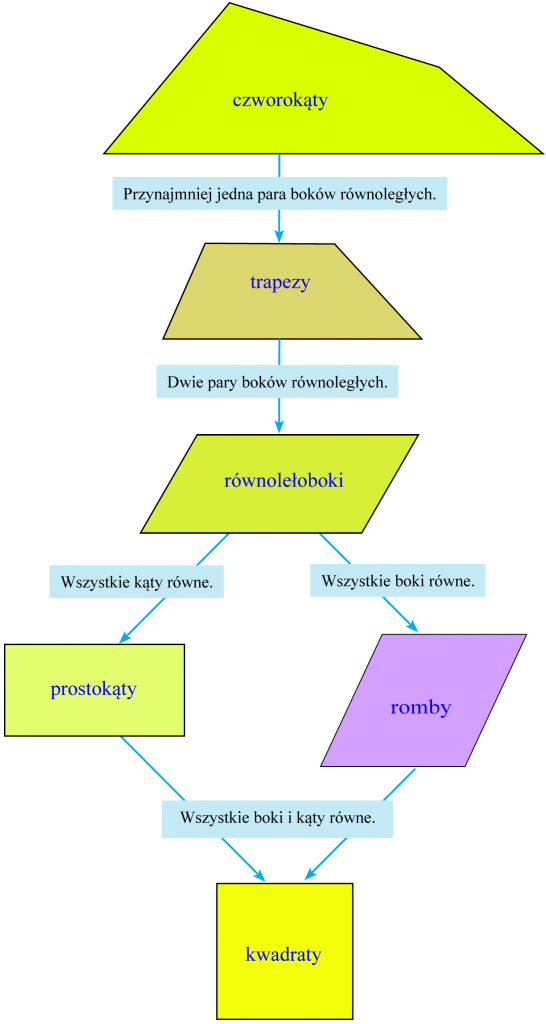
Klasyfikacja czworokątów
Klasyfikacja czworokątów
Sprawdź, ile zapamiętałeś o czworokątach!
1. Wskaż zdanie fałszywe:
A. Każdy kwadrat jest prostokątem.
B. Każdy romb jest trapezem.
C. Każdy trapez jest równoległobokiem.
D. Każdy prostokąt jest równoległobokiem.
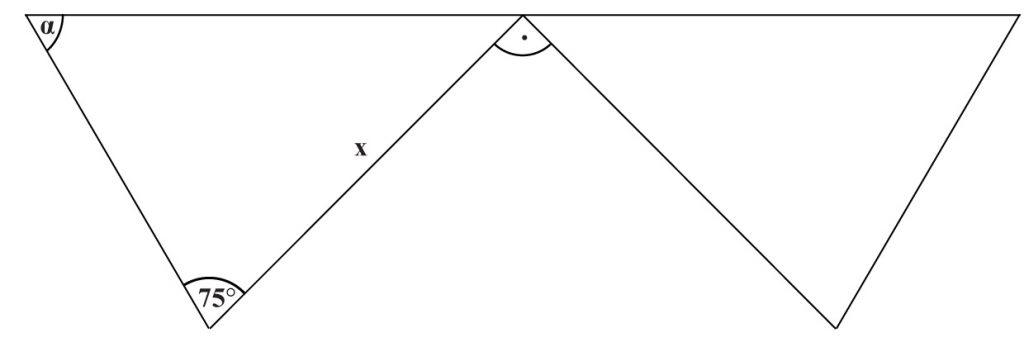
2. Miara kąta α wynosi:
3. Który z czworokątów o podanych miarach dwóch kątów jest rombem:
A. 20°, 80°
B. 75°, 115°
C. 140°, 60°
D. 90°, 90°
4. Sumę miar wszystkich kątów wewnętrznych n-kąta można obliczyć, korzystając ze wzoru (n – 2) · 180° dla n3. Ile wynosi miara jednego kąta wewnętrznego pięciokąta foremnego?
A. 540°
B. 108°
C. 120°
D. 720°
5. Liczbę przekątnych w n-kącie liczymy według wzoru dla n3. W jakim wielokącie liczba przekątnych jest równa liczbie jego boków:
A. w trójkącie,
B. w czworokącie,
C. w pięciokącie,
D. w sześciokącie.
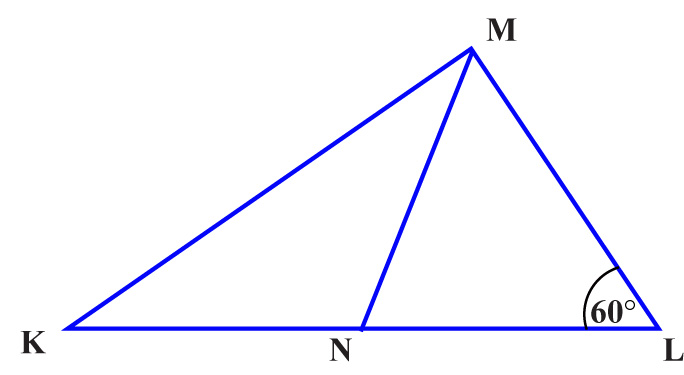
6. Jeżeli IKNI = INLI = INMI, to miara kąta KML wynosi:
A. 30°
B. 60°
C. 90°
D. 120°
Odpowiedzi:
1. C, 2. A, 3. D, 4. B, 5. C, 6. C.