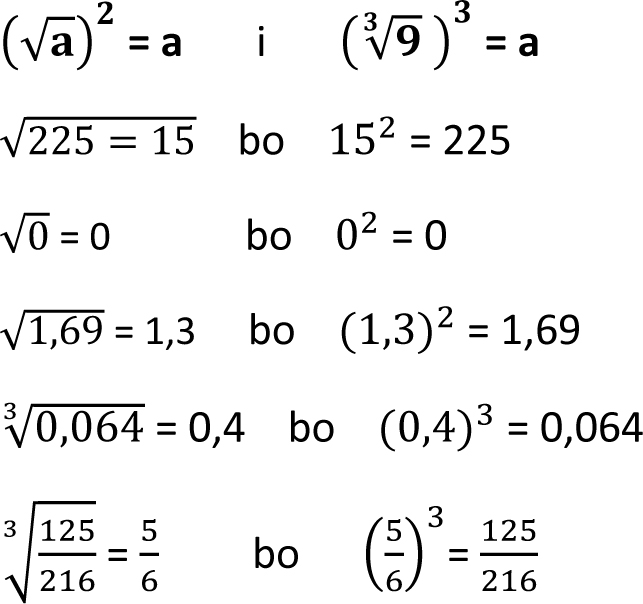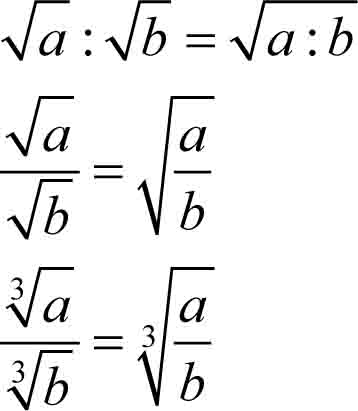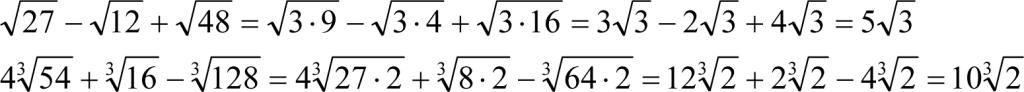Symbol ![]() czytamy: pierwiastek n-tego stopnia z liczby z
czytamy: pierwiastek n-tego stopnia z liczby z
- Liczbę z nazywamy liczbą podpierwiastkową lub pierwiastkowaną.
- Liczbę n nazywamy stopniem pierwiastka.
Pierwiastek n-tego stopnia z liczby a równa się b, gdy b do potęgi n-tej jest równe a.
Uwaga!
Pierwiastek kwadratowy (drugiego stopnia)
dla a ≥ 0, b ≥ 0
Uwaga! Gdy nie ma zapisanego stopnia pierwiastka to wiemy, że jest to pierwiastek 2-go stopnia, czyli pierwiastek kwadratowy. ![]()
Pamiętaj! Najniższy stopień pierwiastka wynosi 2 i, zgodnie z umową, tej dwójki nie piszemy.
Pierwiastek sześcienny (trzeciego stopnia)
dla a ≥ 0, b ≥ 0
Ważne!
Nie określamy pierwiastka z liczby ujemnej.
Zapamiętaj!
- Pierwiastek, którego stopień wynosi 2, nazywamy pierwiastkiem kwadratowym lub pierwiastkiem stopnia drugiego.
- Pierwiastek, którego stopień wynosi 3, nazywamy pierwiastkiem sześciennym lub pierwiastkiem stopnia trzeciego.
- Arytmetycznym pierwiastkiem drugiego stopnia z liczby nieujemnej a nazywamy taką liczbę nieujemną b, która podniesiona do kwadratu równa jest liczbie podpierwiastkowej a.
- Arytmetycznym pierwiastkiem trzeciego stopnia z liczby nieujemnej a nazywamy taką liczbę nieujemną b, która podniesiona do sześcianu równa jest liczbie podpierwiastkowej a.
Z definicji pierwiastka kwadratowego i sześciennego wynika, że:
Pierwiastki jednakowych stopni można mnożyć, dzielić wg następujących wzorów:
dla a≥0 i b≥0
dla a≥0 i b>0
Dodawać lub odejmować pierwiastki możemy tylko wtedy, gdy stopnie pierwiastka są takie same oraz liczby podpierwiastkowe są jednakowe.
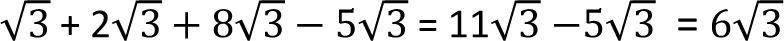
Pod pierwiastek można włączyć czynnik stojący przed pierwiastkiem. Można też wyłączyć czynnik przed znak pierwiastka.
Wyjaśnienie: liczbę podpierwiastkową rozkładamy na iloczyn takich dwóch lub więcej czynników, z których przynajmniej jeden jest kwadratem konkretnej liczby (pod pierwiastkiem kwadratowym) lub sześcianem konkretnej liczby (pod pierwiastkiem sześciennym). Wyliczamy tę liczbę wynosząc ją przed pierwiastek, reszta zaś czynników pozostaje pod pierwiastkiem. Ta czynność potrzebna nam jest przy dodawaniu lub odejmowaniu pierwiastków.
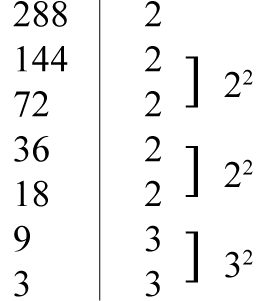
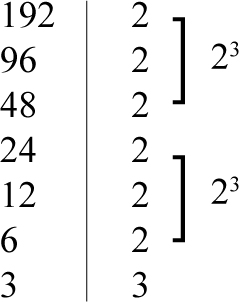
Jeśli trudno nam w pamięci zapisać liczbę w postaci iloczynu odpowiednich czynników, pomagamy sobie wtedy rozkładem liczby na czynniki pierwsze:
Oto typowe zadania z zastosowaniem działań na pierwiastkach:
– występuje tu mnożenie sumy algebraicznej przez jednomian.
b)
– występuje tu dzielenie sumy algebraicznej przez jednomian.
c)
– występuje tu mnożenie sum algebraicznych.
d)
– zastosowanie wzorów skróconego mnożenia.
Bardzo ważną czynnością jest pozbywanie się niewymierności z mianownika ułamka: