Twierdzenie Talesa

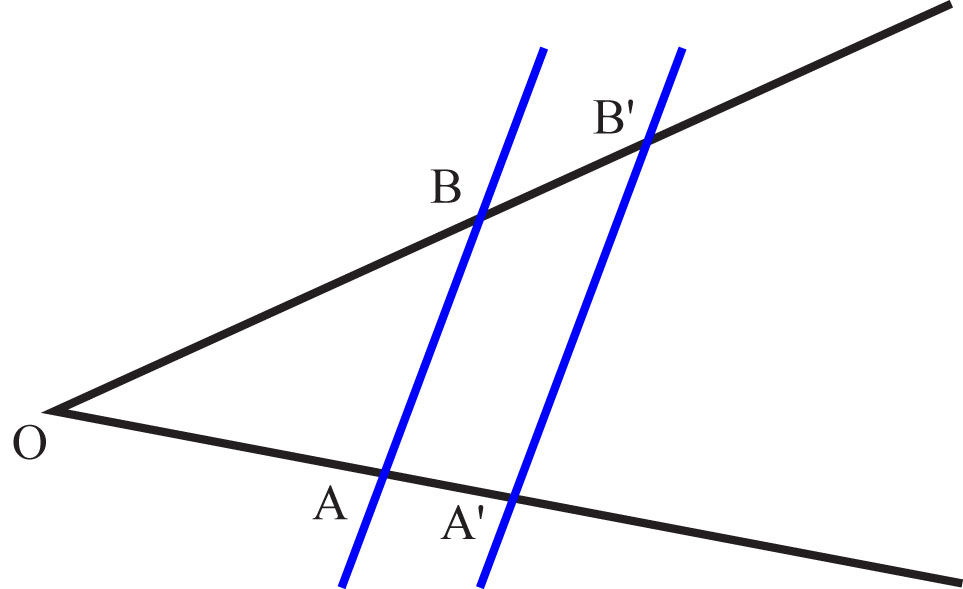
Jeżeli ramiona kąta przetniemy dwiema prostymi równoległymi, to odcinki utworzone na ramionach tego kąta będą proporcjonalne.

Które odcinki będą proporcjonalne?
Sprawdź to na przykładzie!

Ramiona kąta AOB przecięto równoległymi prostymi: AB i A’B’.
Wynika stąd, że prawdziwe są następujące równości:

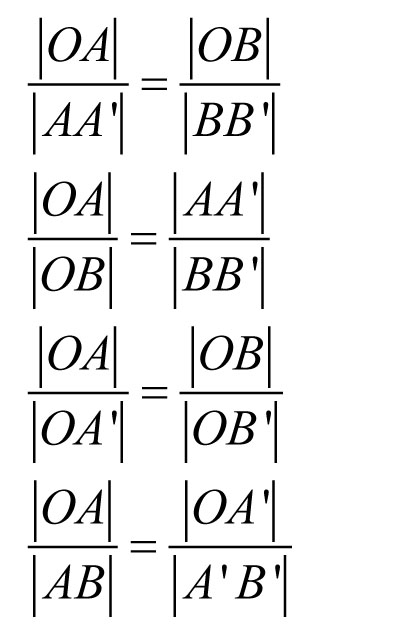
Prawidłowość ta służy do rozwiązywania całej gamy zadań z geometrii.

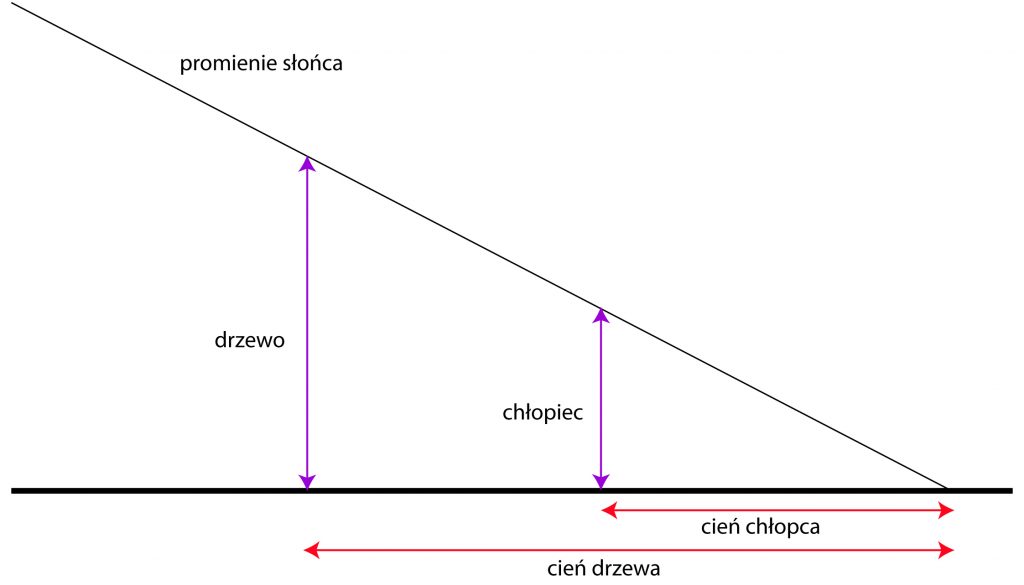
Chłopiec wzrostu 160 cm rzuca cień długości 4 metry. Jednocześnie drzewo rzuca cień długości 37,5 metra. Oblicz wysokość tego drzewa

Promienie słońca tworzą z ziemią pewien kąt. Drzewo i człowiek stoją w liniach równoległych. Schematycznie możemy to zaznaczyć tak:

Tu możesz skorzystać z twierdzenia Talesa, a otrzymasz proporcję:

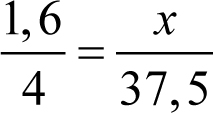
, gdzie x oznacza wysokość drzewa. Stąd otrzymujemy x = 15. Drzewo ma zatem wysokość 15 m.

Uwaga! Podstawiając dane do proporcji, zawsze pamiętaj o uzgodnieniu jednostek (w tym przypadku wszystkie długości podstawiliśmy w metrach).

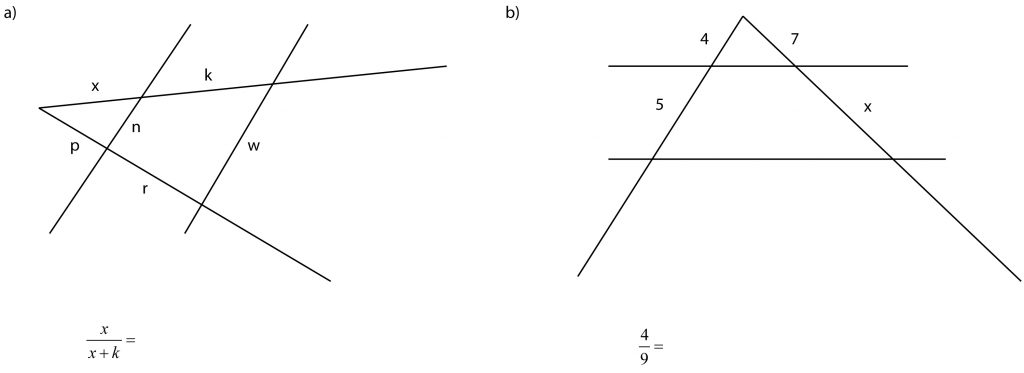
Uzupełnij równanie (dopisując drugą jego stronę) pod każdym z rysunków:

a) Do prawej strony równania można dopisać lub

b) Do prawej strony równania należy dopisać

Wybierz tę parę trójkątów o danych długościach boków, w której obydwa trójkąty są podobne do trójkąta o bokach:

A. i

B. i

C. i

Zauważ, że to odpowiednio: . Zatem trójkąt o takich bokach jest podobny do trójkąta o bokach (stosunki długości odpowiednich boków są równe 7).