1. Czym jest zdanie z punktu widzenia logiki?
Zdanie to pewne stwierdzenie, wyrażone zdaniem pojedynczym, oznajmującym, o którym można powiedzieć, czy jest prawdą, czy też nie. Zdanie w logice oznaczamy symbolem: p, q lub też r.
W logice nie zajmujemy się zdaniami, które mają formę pytań, próśb czy też rozkazów.
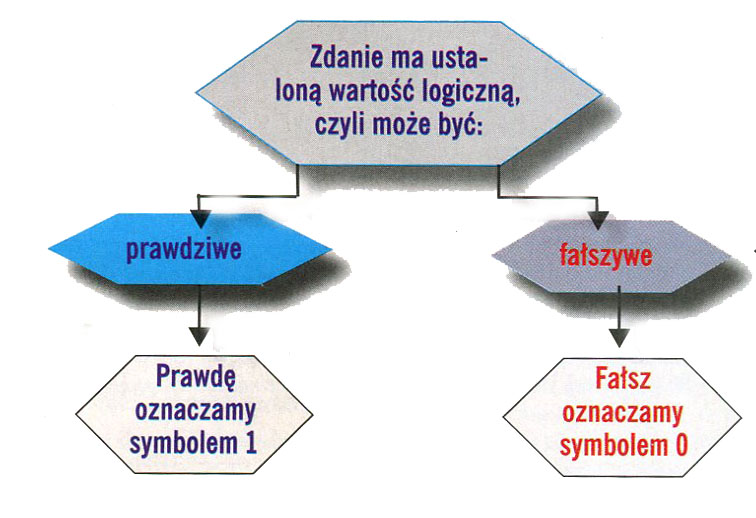
2. Co to jest wartość logiczna zdania?
Wartość logiczna mówi o tym, czy zdanie jest prawdziwe, czy fałszywe.
3. Jak budujemy zaprzeczenie zdania?
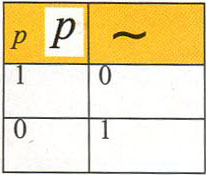
Jeśli przed zdaniem postawimy: nieprawda, że (czyli negację), to zdanie zmieni swoją wartość logiczną na przeciwną. Symbolem negacji jest symbol ~
Spójrz na przykład!
Gdy jesteś uczniem liceum, to możesz powiedzieć o sobie takie zdania:
- Zdanie p: Jestem licealistą.
- Zdanie q: Jestem przedszkolakiem.
Zdanie p ma wartość logiczną 1 (prawda), a zdanie q ma wartość logiczną 0 (fałsz).
Jeśli zbudujesz zaprzeczenia obu tych zdań, to otrzymasz:
- Nieprawda, że jestem licealistą (0) Symbolicznie: ~ p
- Nieprawda, że jestem przedszkolakiem (1). Symbolicznie: ~ q
Negacja zdania prawdziwego staje się fałszem, a negacja zdania fałszywego staje się prawdą!
To, jak działa negacja zdania, można zapisać w tabeli:
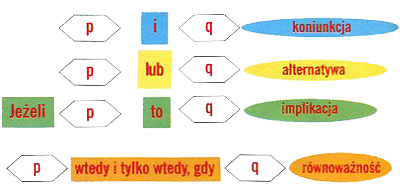
4. Czym jest zdanie złożone?
Zdanie złożone składa się z dwóch zdań pojedynczych połączonych ze sobą spójnikiem. Takie spójniki są cztery:
- „i”,
- „lub”,
- „jeżeli… to…”,
- „wtedy i tylko wtedy, gdy”.
Zdania złożone, zbudowane za pomocą tych spójników, mają swoje nazwy:
- koniunkcja,
- alternatywa,
- implikacja,
- równoważność.
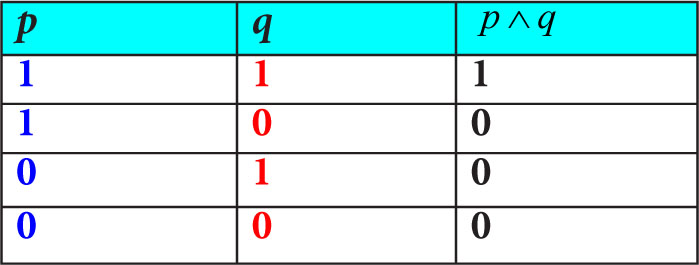
5. Jak określamy wartość logiczną koniunkcji zdań?
Koniunkcja jest prawdą tylko wtedy, gdy oba tworzące ją zdania pojedyncze są prawdziwe. Jeśli przynajmniej jedno ze zdań jest fałszywe, to całe zdanie złożone również nie jest prawdą.
Spójrz na przykład!
Jestem licealistą i jestem dobrym uczniem.
Jeśli oba zdania składowe są prawdziwe, czyli rzeczywiście jesteś licealistą (1) i jesteś dobrym uczniem (1), to koniunkcja takich zdań jest oczywiście prawdą (1). Wystarczy, że jedno z tych zdań będzie fałszywe, czyli: jesteś licealistą (1) i nie jesteś dobrym uczniem (0) lub też nie jesteś licealistą (0) i jesteś dobrym uczniem (1), to wtedy całe zdanie staje się fałszywe (0). Gdy oba zdania są fałszywe, to oczywiście i ich koniunkcja jest fałszem (0).
Koniunkcję zapisujemy symbolicznie: p∧ q
Wszystkie przypadki koniunkcji dwóch zdań, w zależności od ich wartości logicznej (czyli prawdziwości), można przedstawić w tabeli:
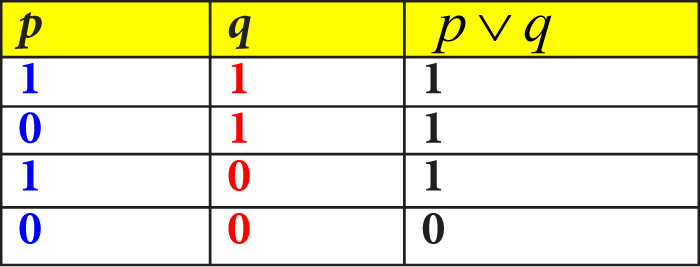
6. Kiedy alternatywa zdań jest prawdą, a kiedy fałszem?
Alternatywa jest prawdą wtedy, gdy przynajmniej jedno ze zdań, które ją tworzą, jest prawdziwe. Alternatywa jest fałszywa tylko wtedy, gdy oba tworzące ją zdania są fałszywe.
Spójrz na przykład!
Jestem licealistą lub jestem dobrym uczniem.
Może więc być tak, że: jesteś licealistą (1) i jednocześnie jesteś dobrym uczniem (1).
Może być też tak, że nie jesteś licealistą (0), ale jesteś dobrym uczniem (1), czy wreszcie jesteś licealistą (1), ale nie jesteś dobrym uczniem (0).
Zdanie złożone będzie fałszywe, gdy ani nie będziesz licealistą (0), ani też nie będziesz dobrym uczniem (0).
Alternatywę zapisujemy symbolicznie: p ∨ q
Opisane przypadki alternatywy dwóch zdań możesz przedstawić w takiej tabeli:
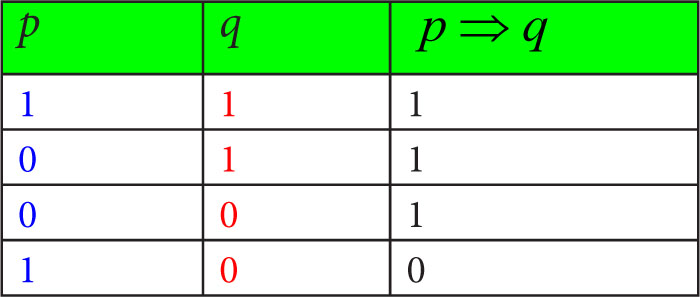
7. Jak określić prawdziwość implikacji?
Implikacja umożliwia wnioskowanie. Na podstawie pierwszego zdania wnioskujemy o prawdziwości drugiego zdania. Pierwsze zdanie nazywamy poprzednikiem implikacji, a drugie zdanie to następnik implikacji.
Z prawdziwego założenia może wynikać wyłącznie prawdziwy wniosek. Z fałszywego założenia mogą jednak wynikać zarówno fałszywe, jak i prawdziwe wnioski. Najprościej zapamiętać, że implikacja jest zawsze prawdziwa z wyjątkiem jednej sytuacji, gdy z prawdy wynika fałsz. Jeśli więc pierwsze ze zdań jest prawdziwe a drugie fałszywe, to całe zdanie złożone staje się fałszywe.
Spójrz na przykład!
Jeśli będziesz dużo umiał, to zdasz egzamin.
Gdy oba zdania składowe są prawdziwe, to i zdanie złożone jest prawdą.
A co będzie wtedy, gdy nie będziesz dużo umiał (0 – pierwsze zdanie fałszywe)? Wtedy, jak to na egzaminie bywa, zdasz egzamin (1) lub też nie zdasz egzaminu (0).
W obu przypadkach zdanie złożone (implikacja) może być prawdą! (1)
Pozostaje jeszcze jedna możliwość: jeśli będziesz dużo umiał (1), to nie zdasz egzaminu (0) i to raczej nie może być prawdą!!! (0)
Implikację zapisujemy symbolicznie: p ⇒ q
Opisane powyżej przypadki można zebrać w tabelce:
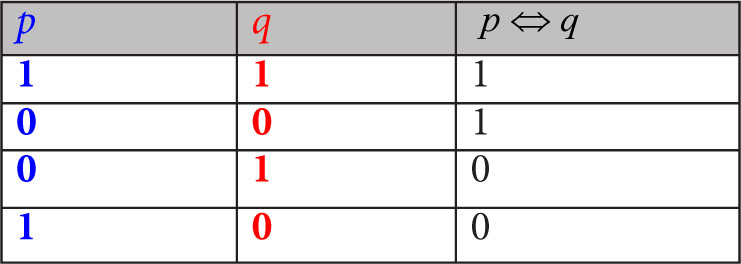
8. Kiedy równoważność jest prawdą?
Równoważność to implikacja w dwie strony. Oznacza to, że jeśli uznamy jedno ze zdań za prawdziwe, to przyjmujemy, że prawdziwe jest i drugie z nich. Jeśli jedno z nich uznamy z fałsz, to musimy uznać również fałszywość drugiego. W obu przypadkach zbudujemy równoważność prawdziwą. Fałszem będzie równoważność, w której jedno ze zdań jest fałszem, a drugie prawdą.
Spójrz na przykład!
Dostanę świadectwo dojrzałości (1) wtedy i tylko wtedy, gdy zdam maturę (1).
W języku potocznym nie używamy tak zawiłego spójnika, jakim jest: „wtedy i tylko wtedy, gdy”, więc powyższe zdanie brzmi dość dziwnie.
Jest oczywiste, że takie zdanie jest prawdą, jeśli oba zdania składowe są prawdziwe.
Ale prawdą będzie również następujące stwierdzenie:
Nie dostanę świadectwa dojrzałości (0) wtedy i tylko wtedy, gdy nie zdam matury (0).
Inne kombinacje są fałszywe, bo nie możesz: dostać świadectwa dojrzałości (1), ale nie zdać matury (0), bądź też nie dostać świadectwa dojrzałości (0), mimo zdanej matury (1).
Równoważność zapisujemy symbolicznie: p ⇔ q
Tabela równoważności wygląda więc tak:
Sprawdź się na zadaniach!
1. Które z podanych stwierdzeń są zdaniami z punktu widzenia logiki?
a) Nieprawda, że liczba 50 dzieli się przez 5.
b) Uzasadnij, że 10 nie jest liczbą pierwszą.
c) Każdy trójkąt ma trzy kąty.
d) Dlaczego czworokąt ma cztery boki?
Rozwiązanie
Zdaniami w logice nie mogą być pytania i polecenia, więc warunków zadania nie spełniają wypowiedzi b) i d). Zdaniem logicznym jest zdanie a), chociaż jest zdaniem fałszywym (jego wartość logiczna wynosi 0). Zdaniem logicznym (i prawdą) jest oczywiście zdanie c).
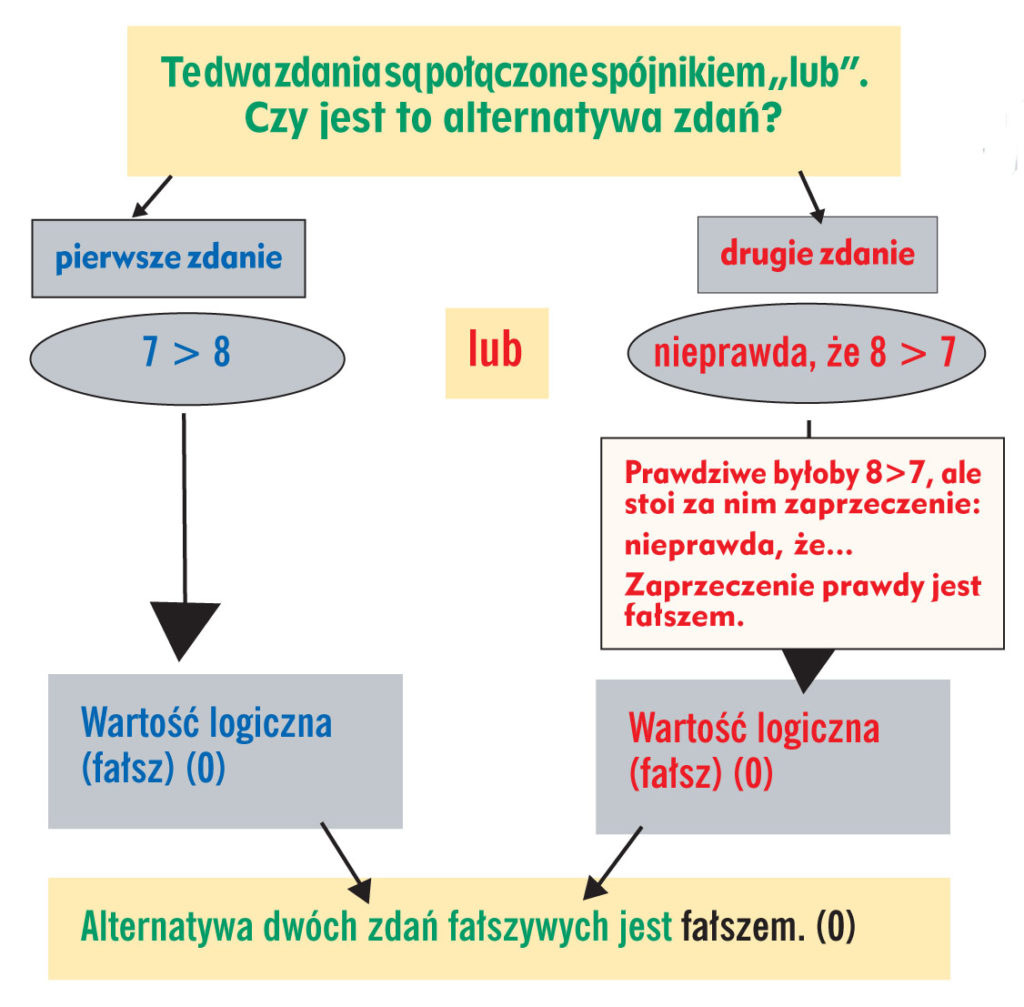
2. Jaka jest wartość logiczna poniższego zdania:
7 > 8 lub nieprawda, że 8 > 7
Rozwiązanie
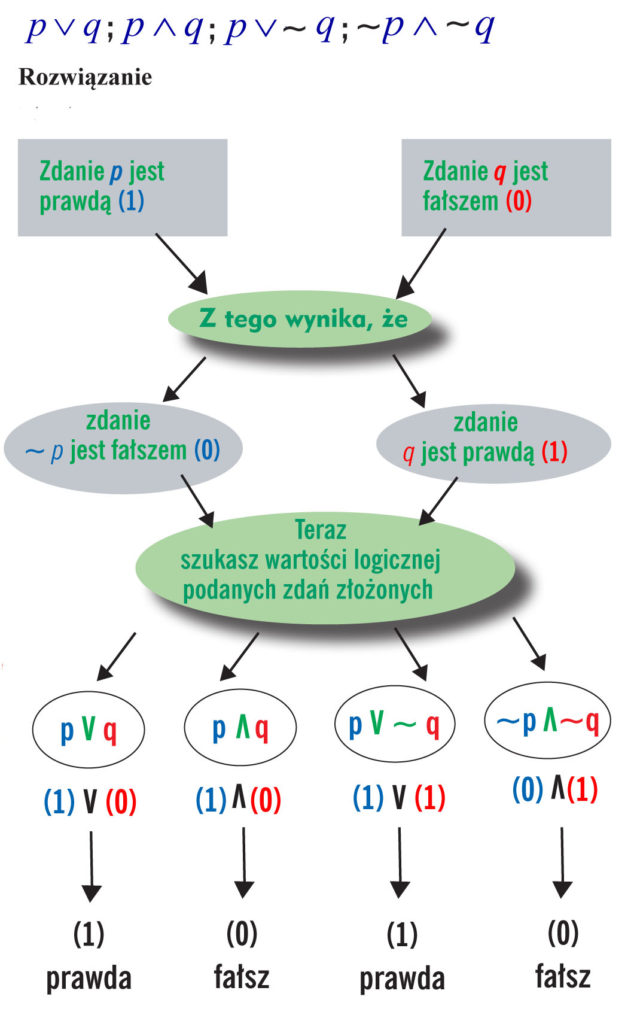
3. Masz dwa następujące zdania:
Zdanie p: 6 jest liczbą parzystą.
Zdanie q: 5 jest liczbą parzystą.
Podaj wartość logiczną następujących zdań:
Musisz umieć!
Stosować zaprzeczenie zdania.
• Określać wartość logiczną: alternatywy, koniunkcji, implikacji i równoważności zdań na konkretnych przykładach,
• Stosować prawa logiki w zadaniach.
Zadanie na maturę
Zbadano społeczność złożoną ze 100 małżeństw i ich dzieci. W wyniku badania otrzymano następujące informacje:
a) 7 małżeństw jest bezdzietnych.
b) Każdy chłopiec ma przynajmniej siostrę.
c) Wśród małżeństw mających dzieci 12 nie ma syna.
d) Pośród dziewcząt jest 9 jedynaczek.
e) Żaden chłopiec nie ma więcej niż 3 siostry.
Sprawdź, czy prawdziwe są zdania:
A. Każdy chłopiec ma siostrę.
B. Żaden chłopiec nie jest jedynakiem.
C. Ponad 80 małżeństw ma co najmniej 2 dzieci.
D. Badane rodziny mają łącznie ponad 170 dzieci.
E. Łączna liczba dzieci w tych rodzinach nie przekracza 360.
Rozwiązanie
Z punktu b) wynika , że prawdziwe jest też zdanie A) oraz B).
Jeśli prawdziwe jest a), to znaczy, że tylko 93 małżeństwa mają dzieci. Z punktu c) wynika, że 81 małżeństw ma syna. Wiemy, że prawdziwe jest B), więc ci, co mają syna, mają jednocześnie co najmniej 2 dzieci, czyli prawdziwe jest C).
Jaka jest łączna liczba dzieci?
81 małżeństw ma nie więcej niż 4 dzieci, co wynika z e). Daje to w sumie nie więcej niż 324 dzieci. Jeśli 12 małżeństw mających dzieci nie ma syna, to mają one córki. Jeśli prawdziwe jest d), to 3 małżeństwa mają więcej niż 1 córkę. Nie mamy informacji, ile córek może być w tych rodzinach. Maksymalnej liczby dzieci nie możemy zatem określić. Nie możemy stwierdzić prawdziwości E). Możemy jedynie powiedzieć, że łączna liczba dzieci jest większa od 324 + 9 = 333.
Jeśli prawdziwe jest b), to 81 małżeństw ma jednocześnie nie mniej niż 2 dzieci. To znaczy, że minimalna liczba dzieci wynosi 162 + 9 jedynaczek (na podstawie d), czyli 171 dzieci. A więc prawdziwe jest D).