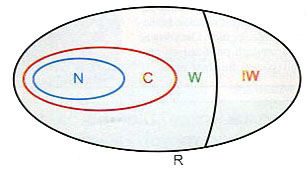
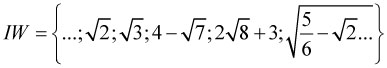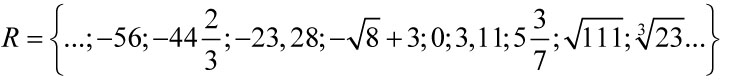Liczby naturalne (symbol: N)
Liczby te zapisujemy za pomocą 10 znaków zwanych cyframi (1, 2, 3, 4, 5, 6, 7, 8, 9, 0).

Liczby całkowite (symbol: C)
Liczby naturalne różne od zera nazywane są także liczbami całkowitymi dodatnimi, np. 1, 2, 3, 4…,
liczby do nich przeciwne są liczbami całkowitymi ujemnymi, np. – 1, – 2, – 3, – 4… Zbiór liczb całkowitych tworzą zatem liczby całkowite ujemne i liczby naturalne.
Skojarz!
Liczby całkowite – ich nazwa już Ci wszytko podpowiada.
Uwaga!
Zero nie jest ani liczbą dodatnią, ani liczbą ujemną.

Liczby wymierne (symbol: W)
Każdą liczbę, którą można przedstawić w postaci ułamka zwykłego,

, gdzie p, q ∈ C, q ≠ O (czytaj: p jest dowolną liczbą całkowitą i q jest liczbą całkowitą, ale różną od zera), nazywamy liczbą wymierną.
Zauważ!
Liczby 0, 4, -6są liczbami wymiernymi, bo:

Liczby niewymierne (symbol: IW)
Mają one swoje miejsce na osi liczbowej, ale nie da się ich przedstawić w postaci ułamka zwykłego, w którym licznik i mianownik są liczbami całkowitymi.
Skojarz liczby niewymierne z pierwiastkami.

Liczby rzeczywiste (symbol: R)
Wszystkie liczby wymierne i niewymierne łącznie nazywamy liczbami rzeczywistymi.

 

1. Zbiory liczb

Zapamiętaj symbole i przykłady liczb!

Zbiór liczb naturalnych:

N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…}

Zbiór liczb całkowitych:

C = {…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4…}

Zbiór liczb wymiernych:

Zbiór liczb niewymiernych:

Zbiór liczb rzeczywistych:

2. Działania na liczbach

Zapamiętaj!!!

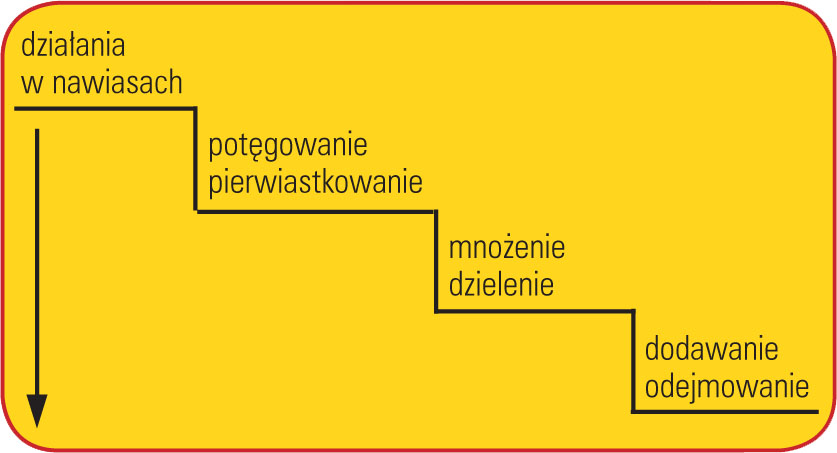
3. Kolejność działań

Zadanie:
Które obliczenie zostało wykonane prawidłowo?

1. Piotr obliczył tak:
3 – 3 · (– 5) = 3 + 15 = 18

2. Paweł inaczej:
3 – 3 · (– 5) = 0 · (– 5) = 0

Jeśli jeszcze nie jesteś pewien, to skacząc schodami w dół po jednym stopniu, przypomnij sobie kolejność wykonywania działań:
Zapamiętaj!

Czy teraz już wiesz, który z chłopców wykonał obliczenia poprawnie? Oczywiście Piotr.

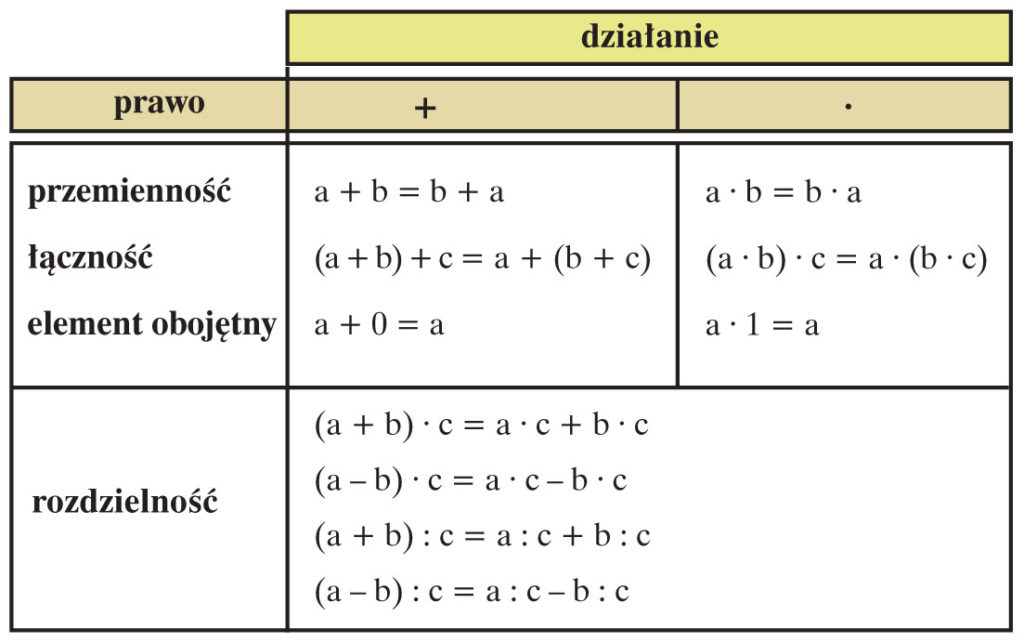
4. Prawa działań, które musisz zapamiętać!

Zauważ!
W Polsce i wielu innych krajach świata używamy do zapisu liczb głównie dziesiątkowego systemu pozycyjnego. Na przykład w zapisie liczby 43434 cyfra 4 występuje trzy razy, a cyfra 3 dwa razy, ale o wartości każdej z tych cyfr decyduje pozycja, jaką ona zajmuje w zapisie liczby. Czytając od strony prawej ku lewej, mamy: cztery jedności, trzy dziesiątki, cztery setki, trzy tysiące, cztery dziesiątki tysięcy. Tę liczbę można zapisać w systemie dziesiętnym jako:
43434 = 4 · 10 000 + 3 · 1000 + 4 · 100 + 3 · 10 + 4 · 1

.

A teraz sprawdzian!

Zadanie 1.
Gospodyni domowa – „Och, te zakupy”

Mama zrobiła listę zakupów w sklepie spożywczym:

Lista zakupów:
1 chleb
5 bułek
1 mleko
30 dag sera żółtego
20 dag cukierków czekoladowych
2 soki WICIO
1 kg mąki
2 kostki margaryny

Cennik:

chleb… 1,45 zł
mleko… 1,40 zł
bułka… 35 gr
mąka… 1,92 zł
margaryna… 1,13 zł
sok WICIO… 98 gr
ser żółty… 15,50 zł/ kg
cukierki czekoladowe… 21,30 zł/ kg

O jakim nominale banknot ma wziąć mama, aby starczyło jej na zakupy i otrzymana w sklepie reszta była najmniejsza? Mama ma do dyspozycji banknoty 10 zł, 20 zł i 50 zł.

Zadanie 2.
Magazynier – „Ile zarobię?”

Pan Stach pracuje w markecie na stanowisku magazyniera. W ciągu dwóch tygodni przepracował 72 godziny płatne po 7,30 zł za godzinę oraz
11 godzin nadliczbowych płatnych razy więcej niż stawka 7,30 zł. Ile zarobił pan Stach w ciągu tych dwóch tygodni?

Zadanie 3.
Ogrodnik – „Chyba źle obliczyłem!”

Ogrodnik kupił 25 m siatki na reperację płotu. Jednego dnia wymienił starą siatkę na nową na odcinku 6,4 m, nazajutrz zaś na odcinku dwa razy dłuższym. Czy pozostała siatka wystarczy mu na reperację płotu na odcinku o 0,5 m krótszym od naprawionego pierwszego dnia? Czy ogrodnik popełnił błąd w obliczeniach?

Zadanie 4.
Turysta – „Hej, hej, przygodo!”

Turysta miał do pokonania trasę długości 180 km. Połowę trasy przejechał autokarem, 1/5 reszty autobusem, a pozostałą część pieszo. Ile co najmniej dni zajmie mu piesza wędrówka, jeżeli dziennie chce pokonywać nie więcej niż 18 km?

 

Jak rozwiązać te zadania?

Znajdziesz tu odpowiedzi do zadań i wskazówki, na co powinieneś zwrócić uwagę.

Zadanie 1.
Ważne! Pamiętaj o zamianie gramów na kilogramy.
Obliczenie do tego zadania można przedstawić za pomocą jednego działania:
1,45 + 5 . 0,35 + 1,40 + 0,3 . 15,50 + 0,2 . 21,30 + 2 . 0,98+ + 1,92 + 2 . 1,13 = 19,65
Oczywiście, aby mamie starczyło na zakupy i otrzymana reszta była najmniejsza, musi wziąć banknot 20 zł.

Zadanie 2.
Najpierw dowiedzmy się, ile zarobił za 72 godziny pracy. Iloczyn liczb 72 i 7,30 zł wynosi 525,60 zł. Teraz musimy wyliczyć, ile wynosiła stawka za godzinę nadliczbową. Mnożąc 1,5 przez 7,30 zł otrzymujemy kwotę 10,95 zł. Ponieważ pan Stach przepracował 11 godzin nadliczbowych, czyli zarobił 11·10,95 zł = 120,45 zł. Zatem łącznie magazynier w markecie za dwa tygodnie otrzyma wynagrodzenie w wysokości 646,05 zł.

Zadanie 3.
Ważne! W tym zadaniu zwróć uwagę na różnicę między „2 razy dłuższy” a „o 0,5 m krótszy”! Ponieważ drugiego dnia naprawiono odcinek dwa razy dłuższy niż dnia pierwszego, czyli zreperowano 12,8 m płotu. Razem przez te dwa dni naprawiono 19,2 m płotu. Do naprawy pozostało 5,9 m płotu. Siatki zatem nie wystarczy, gdyż różnica liczb 25 i 19,2 wynosi 5,8. Ogrodnik wykonał błędne obliczenia.

Zadanie 4.
Ważne! Obliczamy ułamek danej liczby, czyli mnożymy ten ułamek przez tę liczbę.
Trasa pokonana przez turystę autokarem wynosiła 90 km. Pozostało jeszcze do przebycia 90 km. Ponieważ , czyli turysta ma do przejścia pieszo 72 km. Wędrówka ta zajmie mu co najmniej 4 dni.