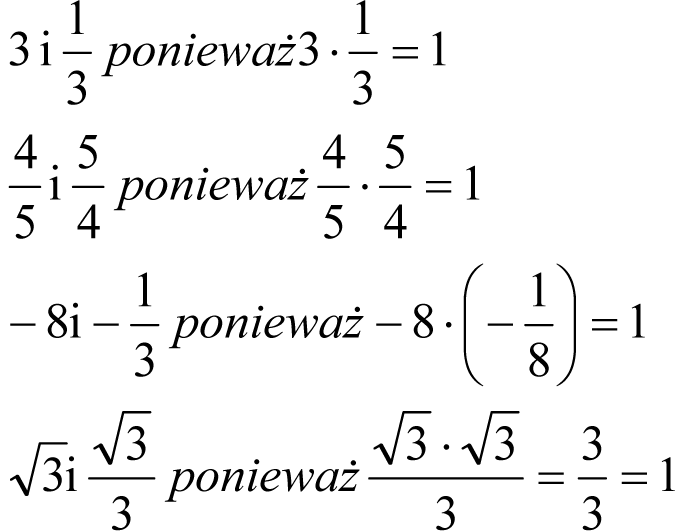• Działania w nawiasach.
  ↓
• Potęgowanie i pierwiastkowanie.
  ↓
• Mnożenie i dzielenie w kolejności zapisu.
  ↓
• Dodawanie i odejmowanie w kolejności zapisu.

Liczba naturalna jest podzielna przez:

• 2 – gdy jej ostatnią cyfrą jest 0, 2, 4, 6, 8, np.:
  (10, 14, 28, 106, 1252);
• 3 – gdy suma jej cyfr jest podzielna przez 3, np.:
  • 66 (bo 6 + 6 = 12, a 12 jest podzielne przez 3)
    
  • 153 (bo 1 + 5 + 3 = 9, a 9 jest podzielne przez 3)
  • 1707 (bo 1 + 7 + 0 + 7 = 15, a 15 jest podzielne przez 3);
    
• 4 – gdy jej dwie ostatnie cyfry tworzą liczbę podzielną przez 4, np.:
  
  • 1264 (bo 64 : 4 = 16)
  • 36 924 (bo 24 : 4 = 6)

Zapamiętaj to inaczej!
– gdy suma cyfr jedności i podwojonej cyfry dziesiątek jest podzielna przez 4, np.: 1556 – jeśli do cyfry jedności (w naszej liczbie to 6) dodamy wynik podwojenia (mnożenia przez 2) liczby dziesiątek (2 • 5 = 10) otrzymamy wynik (6 + 10 = 16), a wiec liczba 16 jest podzielna przez 4 (16 : 4 = 4).

• 5 – gdy jej ostatnią cyfrą jest 0 lub 5;
  • 120, 1350, 11870
  • 125, 2945, 444215;
    
    
• 6 – gdy jest podzielna równocześnie przez 2 i przez 3, np.:
  • 84 (bo 84 : 2 = 42, 84 3 = 28)

Zaamiętaj to inaczej!
– gdy jest parzysta i suma jej cyfr jest podzielna przez 3, np.:
liczba 516 (bo 5 + 1 + 6 = 12), a liczba 12 jest podzielna przez 3 (12 : 3 = 4)
liczba 6714 (bo 6 + 7 + 1 + 4 = 18), a 18 jest podzielne przez 3 (18 : 3 = 6);

• 8 – jej trzy ostatnie cyfry tworzą liczbę podzielną przez 8.
  • 8984 (bo 984 jest podzielne przez 8)

• 9 – gdy suma jej cyfr jest podzielna przez 9, np.:
  • 1017 (bo 1 + 0 + 1 + 7 = 9)
  • 42219 (bo 4 + 2 + 2 + 1 + 9 = 18)
  • 105273 (bo 1 + 0 + 5 + 2 + 7 + 3 = 18);
    
• 10 – gdy jej ostatnią cyfrą jest 0, np.:
  
  • 110, 10020, 16590
    
• 15 – gdy jest podzielna równocześnie przez 3 i przez 5, np.:
  • 1470 (bo jest podzielne zarówno przez 3 (1470 : 3 = 490), jak również przez 5 (1470 : 5 = 294);
    
• 25 – gdy jej dwie ostatnie cyfry to: 00, 25, 50 lub 75, np.:
  
  • 1200, 15325, 8550, 14675;
• 100 – gdy jej dwie ostatnie cyfry są zerami.
  • 125300, 693600

• Liczba a jest wielokrotnością liczby b gdy liczba a dzieli się przez liczbę b bez reszty, np; liczba 36 jest wielokrotnością liczby 6, bo dzieli się przez 6 bez reszty (36 : 6 = 6).
• Liczba c jest dzielnikiem liczby d gdy liczba d dzieli się przez liczbę c bez reszty, np; 8 jest dzielnikiem 64, bo 64 dzieli się przez 9 bez reszty.

• Liczby pierwsze to takie liczby naturalne większe od 1, które mają tylko dwa dzielniki: 1 i samą siebie.
  Liczby 7 i 23 są liczbami pierwszymi, ponieważ:
  D₁₇ = {1,7}, D₂₃ = {1,23}
• Liczby złożone to takie liczby naturalne większe od 1, które mają więcej niż dwa dzielniki. Np. liczby 20 i 49 są liczbami złożonymi, ponieważ:
  • D₂₀ = {1,2,4,5,10,20},
  • D49 = {1,7,49

Uwaga! Liczby 0 i 1 nie są ani pierwsze, ani złożone.

Rzymianie używali do zapisu liczb następujących znaków:

• I = 1; II = 2; III = 3; IV = 4; V = ; VI = 6; VII = 7; VIII = 8,; IX = 9,
• X = 10; XI = 11; XII = 12; XIV = 14; XV = 15, XVI = 16; XVII = 17; XIX = 19;
• XX = 20; XXII = 22; XXIV = 24; XXV = 25; XXVII = 27; XXIX = 29
• XXX = 30; XXXI = 31, XXXIV = 34; XXXV = 35; XXXVIII = 38; XXXIX = 39
  
• XL = 40; XLIII = 43; XLIV = 44; XLV = 45; XLVII = 47; XLIX = 49
  
• L = 50; LI = 51; LIII = 53; LIV = 54; LV = 55; LVII = 57; LIX = 59;
• LX = 60; LXII = 62; LXIV = 64; LXV = 65; LXVI = 66, LXIX = 69;
• LXX = 70; LXXVIII = 78; LXXIX = 79;
• LXXX = 80; LXXXIV = 84; LXXXVIII = 88; LXXXIX = 89;
• XC = 90; XCVII = 97; XCIX = 99;
  
• C = 100; CII = 102; CXLVIII = 148, CXCIV = 194;
• CC = 200; CCIV = 204; CCXLVIII = 248;
• CCC = 300; CCCXCIV = 394;
• CD = 400;
  
• D = 500,
• DCC = 700; DCCC = 800
  
• CM = 900;
• M = 1000; MXII = 1012; ML = 1050; MLXX = 1070;
  
  
• MMM = 3000

• Liczby dziesiętne to liczby, w których zapisie występuje przecinek. Oddziela on całości od części ułamkowych. Przykład: 1,23; 23,02; 159,7
• Liczby dziesiętne dodajemy i odejmujemy sposobem pisemnym tak samo jak liczby naturalne. Podpisujemy jedności pod jednościami, części dziesiąte pod dziesiątymi (podpisujemy przecinek pod przecinkiem).
  22,23 2697,56 187,3205
  + 125,58 – 235,96 + 23,1085
  147,81 2461,6 210,429
  
  
• Mnożąc liczbę dziesiętną przez 10, 100, 1000, 10000… przesuwamy przecinek o jedno, dwa trzy, cztery miejsca w prawo.
  • 10 • 2,0115 = 20,115
  • 100 • 2,0115 = 201,15
  • 1000 • 2,0115 = 2011,5
  • 10000 • 2,0115 = 20115

• Dzieląc liczbę dziesiętną przez 10, 100, 1000, 10000… przesuwamy przecinek o jedno, dwa trzy, cztery miejsca w lewo.
  • 2131,19 : 10 = 213,119
  • 2131,19 : 100 = 21,3119
  • 2131,19 : 1000 = 2,13119
    
  • 2131,19 : 10000 = 0.,213119

• Mnożenie liczby dziesiętnej przez liczbę naturalną wykonujemy podobnie jak mnożenie liczb naturalnych. W iloczynie jest tyle cyfr po przecinku, ile w liczbie dziesiętnej.
  • 5 • 21,41 = 107,05
  • 6 • 26,159 = 156,954
  • 9 • 56,5874 = 509, 2866

• Dzielenie liczby dziesiętnej przez liczbę naturalną wykonujemy podobnie jak dzielenie liczb naturalnych, a przecinek stawiamy nad przecinkiem.
  129,33 697,37 187,986
  : 3 : 5 : 5
  43,11 139,474 37,5972
  

• Mnożenie liczb dziesiętnych wykonujemy podobnie jak mnożenie liczb naturalnych. W iloczynie jest tyle cyfr po przecinku, ile w obu czynnikach razem. 129,33 697,37 187,986 187,986 187,986
  • 22,13 • 3,661 • 1,5897 • 0,15897 • 0,015897
  2862,0729 2553,07157 298,8413442 29,88413442 2,988413442

• Aby podzielić dwie liczby dziesiętne, należy pomnożyć dzielną i dzielnik przez 10, albo przez 100, albo przez 1000, albo …, tak aby dzielnik stał się liczbą całkowitą i dopiero wtedy wykonać dzielenie.
  
  • 5,35 : 0,5 = (mnożymy obie liczby przez 10, aby dzielnik nie był liczbą dziesiętną)
    53,5 : 5 = 8,7
  • 12,419 : 0,22 = (mnożymy obie liczby przez 100, aby dzielnik nie był liczbą dziesiętną)
    1241,9 : 22 = 56,45
  • 35,795 : 7,159 = (mnożymy obie liczby przez 1000, aby dzielnik nie był liczbą dziesiętną)
    35795 : 7159 = 5

_{kreska ułamkowa →} 3 ← licznik ułamka
5 ← mianownik ułamka

• Ułamek właściwy to ułamek, którego licznik jest mniejszy od mianownika.2 5 8 15
  3 10 20 45

• Ułamek niewłaściwy to ułamek, którego licznik jest większy od mianownika albo mu równy.6 85 1206 32 19
  

• Liczba mieszana to liczba, która składa się z liczby całkowitej i ułamka właściwego.₂ 3 ₁₀ 6
  5 8

• Porównywanie ułamkówAby dodać dwa ułamki o takich samych mianownikach, należy dodać ich liczniki, a mianownik pozostawić bez zmian.
  2 ₊ 6 ₌ 8
  9 9 9
  
  • Jeżeli ułamki mają jednakowe mianowniki, to większy jest ten, który ma większy licznik.
    4 _> 2
    8 8
  • Jeżeli ułamki mają jednakowe liczniki, to większy jest ten, który ma mniejszy mianownik.
    4 _< 4
    8 6
    

• Aby odjąć dwa ułamki o takich samych mianownikach, należy odjąć ich liczniki, a mianownik pozostawić bez zmian.5 _– 2 ₌ 3
  8 8 8
  

• Rozszerzanie ułamka polega na pomnożeniu licznika i mianownika ułamka przez tę samą liczbę różną od zera.
  2 ₌ 2 • 3 ₌ 6
  3 3 • 3 9

• Skracanie ułamka polega na podzieleniu licznika i mianownika ułamka przez tę samą liczbę.16 ₌ 16 : 4 ₌ 4
  24 24 : 4 6

• Aby porównać ułamki o różnych mianownikach, można je rozszerzyć lub skrócić tak, aby miały jednakowe liczniki albo mianowniki.Aby dodać albo odjąć ułamki o różnych mianownikach, najpierw sprowadzamy je do wspólnego mianownika, a potem wykonujemy dodawanie albo odejmowanie.6 ₊ 10 ₌ 12 ₊ 10 ₌ 4
  8 16 16 16 6
  Zauważ! Aby sprowadzić oba ułamki do wspólnego mianownika (16) trzeba przemnożyć liczni i mianownik ułamka 6/8 przez 2.
  

• Aby pomnożyć liczbę naturalną przez ułamek albo ułamek przez liczbę naturalną, należy pomnożyć tę liczbę przez licznik ułamka, a mianownik pozostawić bez zmian.6 _{• 6 =} 36
  8 8

• Aby pomnożyć liczbę mieszaną przez liczbę naturalną. należy liczbę mieszaną zamienić na ułamek niewłaściwy, a potem wykonać mnożenie.₂ 3 _{• 6 =} 13 _{• 6 =} 78 _{= 15} 3
  5 5 5 5
  

• Aby pomnożyć ułamek przez ułamek należy pomnożyć licznik przez licznik i mianownik przez mianownik. 2 _• 6 ₌ 12
  9 9 81
  

• Aby podzielić ułamek przez ułamek, należy pomnożyć pierwszy z nich przez odwrotność drugiego, czyli dzielną pomnożyć przez odwrotność dzielnika. 2 _: 5 ₌ 2 • 8 ₌ 16
  9 8 9 • 5 45
  

• Aby podzielić ułamek przez liczbę naturalną, należy pomnożyć jego mianownik przez tę liczbę, a licznik pozostawić bez zmian.6 _{: 6 =} 6 ₌ 6
  8 8 • 6 48
  

• Aby obliczyć ułamek liczby, należy pomnożyć ułamek przez tę liczbę.2 _{liczby 15 to:} 2 • 15 ₌ 30 _{= 10}
  3 3 3
  

• Aby przedstawić ułamek zwykły w postaci dziesiętnej, czyli znaleźć jego rozwinięcie dziesiętne, można:
  • przekształcić go na ułamek o mianowniku 10, 100, 1000, … a następnie zapisać w postaci dziesiętnej3 ₌ 3 • 25 ₌ 75 _{= 0,75}
    4 4 • 25 100
    
  • podzielić licznik przez mianownik3 _{= 3 : 6 = 0,5}
    6

Uwaga! Niektóre liczby mają rozwinięcia dziesiętne, w których bez końca powtarzają się pewne układy cyfr, np.
I _{= 0,33333333…}
3

29 _{= 0,527272727…}
55

Takie nieskończone rozwinięcie dziesiętne nosi nazwę rozwinięcia okresowego, a najmniejszą, powtarzającą się, grupę cyfr nazywamy okresem. W zapisie rozwinięcia okres jest zaznaczany nawiasem.

I _{= 0,33333333… = 0,(3)}
3

29 = 0,527272727… = 0,5(27)
55

Procenty

Aby obliczyć procent danej liczby, należy zamienić procent na ułamek, a następnie pomnożyć go przez daną liczbę, np.
3% liczby 25 to 3/100 liczby 25 : 3 • 25 = 75
100 100 100

Wyrażenia algebraiczne

Wyrażenia algebraiczne to wyrażenia, w których występuje zapis literowy, np.

2a + 3b; 4(a – b); 5c.

Aby obliczyć wartość wyrażenia algebraicznego należy podstawić w miejsce liter odpowiednie liczby.

Układ współrzędnych

Układ współrzędnych tworzą dwie prostopadłe osie liczbowe (oś x i oś y). Położenie każdego punktu w układzie współrzędnych można opisać za pomocą pary liczb – współrzędnych tego punktu.

Zawsze jako pierwszą podajemy współrzędną x.

Średnia arytmetyczna

Aby obliczyć średnią arytmetyczną kilku liczb, należy dodać te liczby, a następnie otrzymaną sumę podzielić przez ilość tych liczb. np. średnia arytmetyczna liczb: 2, 10, 15, 23 to:

2 + 10 + 15 + 33
to

2 + 10 + 15 + 33 ₌ 60 _{= 15}
4 4

Skala

Skala określa, ile razy wymiary na rysunku są powiększone albo pomniejszone w stosunku do wymiarów w rzeczywistości.

• Skala 150 : 1 – powiększenie 150 razy.
• Skala 1 : 1 – rysunek naturalnej wielkości.
• Skala 1 : 500 – zmniejszenie 500 razy.
  

Liczby odwrotne, ujemne, przeciwne

Liczby odwrotne to takie dwie liczby, których iloczyn wynosi 1, np.

Liczby ujemne to liczby, które leżą na osi liczbowej po lewej stronie zera. Np. –8, – 6, – 4, – 2, – 1

Uwaga! Liczba zero nie jest ani liczbą dodatnią, ani liczbą ujemną.
Z dwóch liczb ujemnych ta jest większa, która jest bliżej zera. Np. –6 < –4; –12 < –9.

Liczby przeciwne leżą na osi liczbowej w tej samej odległości od zera, po przeciwnych jego stronach.

Np. 3 i –3, –6 i 6, –28 i 28.

Uwaga! Liczbą przeciwną do 0 jest 0.
Wynikiem dodawania liczb przeciwnych jest liczba 0.

8 + (–8) = 0

Jednostki czasu

• 1 godzina – l h
• 1 minuta – l min
• 1 sekunda – 1 s
• Kwadrans ma 15 minut
• 1h=60min 1 min = 60 s
• Jeden wiek trwa 100 lat.
  
• Zwykły rok ma 365 dni, rok przestępny ma 366 dni.
• Rok ma 52 pełne tygodnie.

Jednostki długości

• 1 km = 1 000 m
• 1 m = 10 dm = 100 cm
• 1 dm = 10 cm
• 1 cm = 10 mm
• 1 kilometr – 1 km
• 1 metr – 1 m
• 1 decymetr – 1 dm
• 1 centymetr – 1 cm
• 1 milimetr – 1 mm

Jednostki masy

• 1 kg = 100 dag
• 1 dag = 10 g
• 1 kg = 1000 g
• 1 kilogram – 1 kg
• 1 dekagram – 1 dag
• 1 gram – 1 g

Jednostki pola

Pola figur wyrażamy w różnych jednostkach: mm², cm², dm², m²

• 1 cm² = 100 mm²
• 1 dm² = 100 cm² = 10 000 mm²
• 1 m² = 100 dm² = 10 000 cm² = 1 000 000 mm²

Przy określaniu powierzchni gospodarstw rolnych, państw itp. Posługujemy się większymi jednostkami:

• arem (a) = 10×10 m (100 m²)
• hektarem (ha )= 100×100 m (10 000 m²)
  
• kilometrem kwadratowym (km²)
  1 km² = 100 ha = 10 000 a = 1 000 000 m²

Jednostki objętości

Do mierzenia objętości brył wykorzystuje się różne jednostki:

Potęga

Iloczyn dwóch lub więcej takich samych czynników możemy zapisać krócej w postaci potęgi:

Pierwiastek

• Taka liczba dodatnia, której druga potęga jest równa 9, nosi nazwę pierwiastka drugiego stopnia z 9 albo pierwiastka kwadratowego z 9.
  
  Uwaga! Liczba pod znakiem pierwiastka nie może być liczbą ujemną. Wartość pierwiastka jest zawsze liczbą dodatnią lub zerem.

• Taka liczba dodatnia, której trzecia potęga jest równa 64, nosi nazwę pierwiastka trzeciego stopnia z 64 albo pierwiastka sześciennego z 64.
  
  

Liczby całkowite

Liczby całkowite to liczby naturalne i liczby do nich przeciwne.

• Iloczyn dwóch liczb o takich samych znakach jest liczbą dodatnią.
  3 • 5 = 15 (-3) • (-5) = 12

• Iloczyn dwóch liczb o różnych znakach jest liczbą ujemną.
  2 • (-3) = -6 (-2) • 3 = -6

Zapamiętaj!

• Iloraz dwóch liczb o takich samych znakach jest liczbą dodatnią.
  15 : 3 = 5 (-15) : (-3) = 5

• Iloczyn, w którym jest parzysta liczba czynników ujemnych jest dodatni.

• Iloczyn, w którym jest nieparzysta liczba czynników ujemnych jest ujemny.

• Iloraz dwóch liczb o różnych znakach jest liczbą ujemną. 20 : (-4) = -5 (-20) : 4 = -5

• Uwaga! Zamiast odejmować liczbę, można dodać liczbę do niej przeciwną.
  15 – (-4) = 15 + 4 = 19
  6 – 10 = 6 + (-10) = -4
  

Podstawowe figury geometryczne

Podstawowe figury geometryczne to:

• punkt,
• odcinek,
• półprosta,
• prosta.

Punkty oznacza się używając dużych liter np. punkty A, B, C.

• A

Odcinek to część prostej, oznacza się go w następujący sposób:

Proste oznaczamy małymi literami, np.:

Półproste oznaczamy za pomocą nazw punktów, przez które przechodzi, np: półprosta PR.

Kąty

Kąt to część płaszczyzny ograniczona dwoma półprostymi o wspólnym początku, wraz z tymi półprostymi.

Kąt półpełny to kąt, którego ramiona są swoimi przedłużeniami. Kąt półpełny ma 180°.

Kąt pełny złożony jest z dwóch kątów półpełnych. Kąt pełny ma 360° (obejmuje całą płaszczyznę.

Kąt zerowy – jego ramiona pokrywają się i jego wnętrze jest zbiorem pustym (nie obejmuje żadnego wycinka płaszczyzny).

Kąt rozwarty to kąt większy od kąta prostego, ale mniejszy od kąta półpełnego. Kąt rozwarty ma więcej niż 90°, a mniej niż 180°.

Kąt większy od kąta półpełnego to kąt wklęsły.

Kat prosty ma rozwartość 90°.

Kąt ostry to kąt mniejszy od kąta prostego. Kąt ostry ma mniej niż 90°, a więcej niż 0°.

Uwaga! Rozwartość kąta mierzymy za pomocą kątomierza.
Jednostką rozwartości kąta nazywamy stopniem i oznaczamy ° (45°).

Nazwa kąta zawiera litery oznaczające trzy punkty: punkt leżący na jednym z ramion, wierzchołek i punkt leżący na drugim ramieniu kąta.

Kąty przyległe mają wspólne ramię i wspólny wierzchołek, a ich pozostałe ramiona są swoimi przedłużeniami.

Kąty AOC i BOC to kąty przyległe.

Zapamiętaj! Suma rozwartości kątów przyległych wynosi 180°.

Kąty wierzchotkowe mają wspólny wierzchołek, a ich ramiona wzajemnie się przedłużają.

Kąty α i β to kąty wierzchołkowe. Kąty wierzchotkowe są równe.
Kąty naprzemianległe są parami równe.

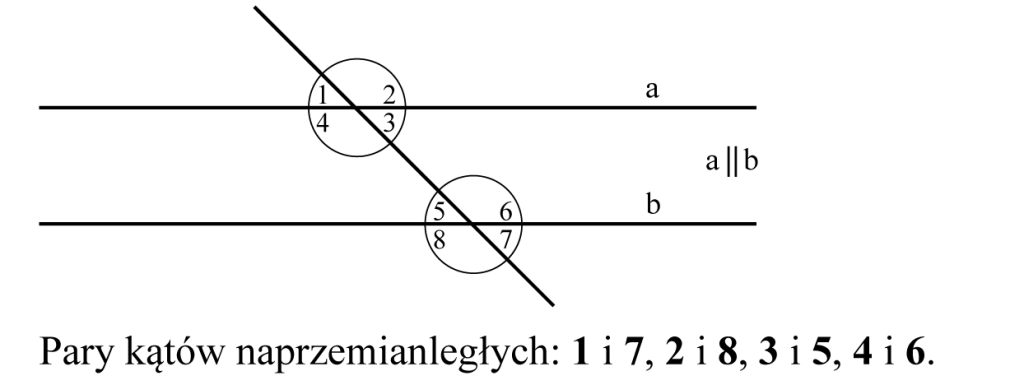
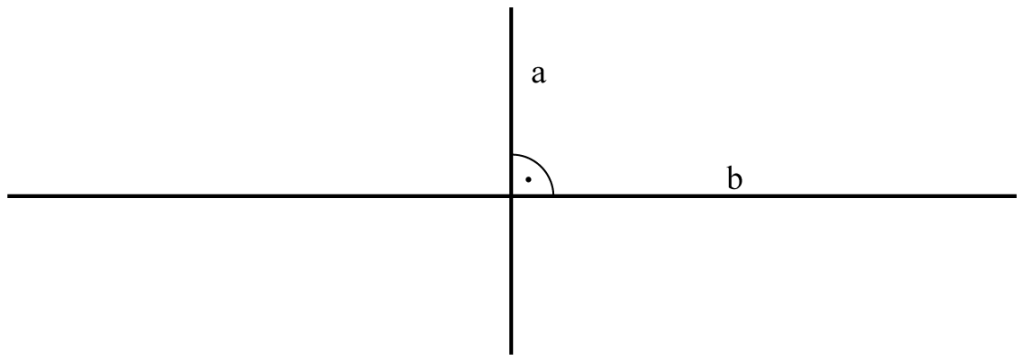
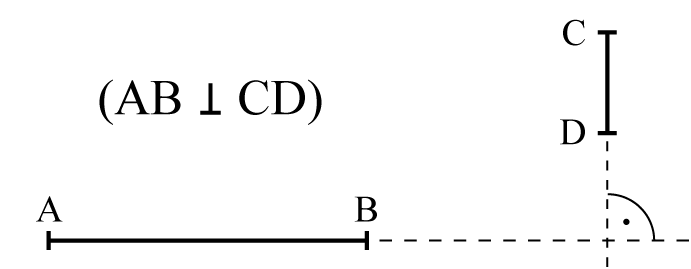
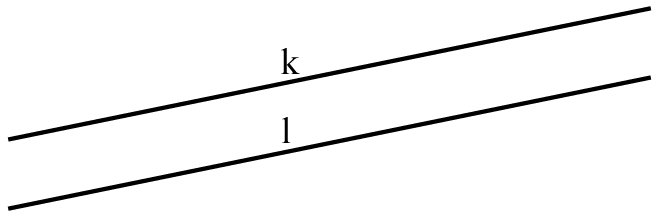
Prostopadłość odcinków i prostych

Proste a i b są prostopadłe, jeśli przecinają się pod kątem prostym.

Dwa odcinki AB i CD są prostopadłe, jeśli odcinki te lub ich przedłużenia przecinają się pod kątem prostym.

Równoległość odcinków i prostych

Proste k i l są równoległe, jeśli się nie przecinają.

Dwa odcinki AB i CD są równoległe, jeśli proste, na których te odcinki leżą, są do siebie równoległe.

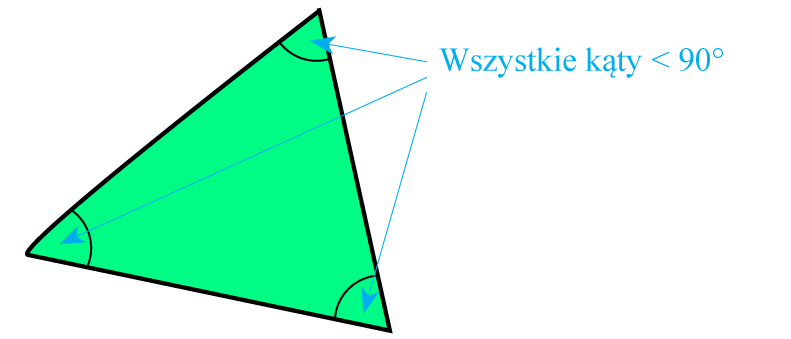
Trójkąty

Trójkąty mają trzy kąty, trzy boki i trzy wierzchołki.

Podział trójkątów ze względu na długość boków

Trójkąt różnoboczny – trójkąt o trzech bokach różnej długości.

Trójkąt równoramienny – trójkąt, który ma chociaż dwa boki równej długości. Kąty przy podstawie trójkąta równoramiennego są równe. Trójkąt równoramienny ma jedną oś symetrii.

Trójkąt równoboczny – trójkąt, który ma wszystkie boki równej długości. Trójkąt równoboczny ma trzy osie symetrii. Wszystkie kąty trójkąta równobocznego są równe.

Zapamiętaj! W każdym trójkącie suma długości dwóch dowolnych boków jest większa od długości trzeciego boku.

Podział trójkątów ze względu na kąty

Trójkąt ostrokątny – trójkąt, który ma wszystkie kąty ostre.

Trójkąt prostokątny – trójkąt, który ma jeden kąt prosty. Boki leżące przy kącie prostym to przyprostokątne.

Trójkąt rozwartokątny – trójkąt, który ma jeden kąt rozwarty.

Zapamiętaj!
Suma rozwartości kątów dowolnego trójkąta równa jest 180°.
Wysokość trójkąta to odcinek łączący wierzchołek z przeciwległym bokiem trójkąta albo przedłużeniem tego boku i prostopadły do niego.

Bok trójkąta, do którego poprowadzona jest wysokość, nazywamy podstawą.

Zapamiętaj! Każdy trójkąt ma trzy wysokości.

Czworokąty

• Czworokąty mają
  • cztery kąty,
  • cztery bok,
  • cztery wierzchołki.

Prostokąt to czworokąt, który ma wszystkie kąty proste.

• Przeciwległe boki prostokąta są parami równe i równoległe.
• Ma dwie przekątne równej długości, które przecinają się w połowie. Ma dwie osie symetrii.

Kwadrat to prostokąt, który ma wszystkie boki równej długości.

• Ma dwie przekątne równej długości, które przecinają się w połowie pod kątem prostym.
• Ma cztery osie symetrii. Każdy kwadrat jest prostokątem.
  

Równoległobok to czworokąt, który ma dwie pary przeciwległych boków równych i równoległych.

• W równoległoboku przeciwległe kąty są parami równe, a suma rozwartości dwóch sąsiednich kątów wynosi 180°.
• Przekątne równoległoboku dzielą się na połowy.
  

Romb to równoległobok, którego wszystkie boki są równej długości.

• Jego przekątne przecinają się pod kątem prostym i dzielą się na połowy.
• Romb, który nie jest kwadratem ma dwie osie symetrii.

Trapez to czworokąt, który ma chociaż jedną parę boków równoległych.

• Trapez, który ma przynajmniej dwa kąty proste to trapez prostokątny.
• Trapez, który ma oś symetrii przechodzącą przez środki obu podstaw to trapez równoramienny. Ma on równe ramiona i dwie pary równych kątów.

Zapamiętaj! Suma rozwartości kątów dowolnego czworokąta równa jest 360°.

Koło i okrąg

Koło to zbiór punktów na płaszczyźnie znajdujących się w odległości mniejszej bądź równej długości promienia.

Okrąg to zbiór wszystkich punktów na płaszczyźnie, położonych w odległość r (długość promienia) od ustalonego punktu (zwanego środkiem okręgu). Można powiedzieć, że okrąg to brzeg koła.

OE (r) — promień; CD — cięciwa; AB — średnica okręgu

Cięciwa to odcinek, który łączy dwa punkty okręgu. Cięciwa dzieli okrąg na dwa łuki.

Średnica to cięciwa przechodząca przez środek okręgu. Jest ona najdłuższą z cięciw.
Średnica dzieli koło na dwa półkola, a okrąg na dwa półokręgi.

Wielokąty foremne

Wielokąt foremny to taki wielokąt, który ma wszystkie boki tej samej długości i wszystkie kąty równe, np.

Oś symetrii figury

Oś symetrii figury to taka linia, który dzieli figurę na dwie identyczne części będące swoimi lustrzanymi odbiciami, np. prostokąt ma 2 osie symetrii, kwadrat ma 4 osie symetrii, koło ma nieskończenie wiele osi symetrii.

Figury przystające

Figury przystające to takie dwie figury, które można na siebie nałożyć, tak aby się dokładnie pokryły.

Gdy dwa wielokąty są przystające, wtedy:

• odpowiednie boki mają jednakową długość,
• odpowiednie kąty mają jednakową rozwartość.

Symetralna odcinka i dwusieczna kąta

Symetralna odcinka to prosta, która jest prostopadła do odcinka i przechodzi przez jego środek.
Każdy punkt symetralnej odcinka leży w tej samej odległości od obu końców tego odcinka.

Dwusieczna kąta to półprosta, o początku w wierzchołku kąta, która dzieli ten kąt na dwa kąty przystające.

Bryły

Prostopadłościan

Prostopadłościan to bryła, której wszystkie ściany są prostokątami. Ma on 6 ścian (2 podstawy i 4 ściany boczne), 8 wierzchołków i 12 krawędzi. Ściany boczne są prostopadłe do podstaw.

Objętość prostopadłościanu obliczamy mnożąc przez siebie jego długość, szerokość i wysokość.

V = a • b • c

a, b, c – długość krawędzi prostopadłościanu

Pole powierzchni prostopadłościanu jest sumą pól wszystkich jego ścian. Można je obliczyć według wzoru:

P = 2ab + 2bc + 2ac

a, b, c – długość krawędzi prostopadłościanu

Sześcian

Sześcian to prostopadłościan, którego wszystkie ściany są kwadratami.

Objętość sześcianu obliczamy ze wzoru:

V = a • a • a

a – długość krawędzi sześcianu

Pole powierzchni sześcianu obliczamy ze wzoru:

a – długość krawędzi sześcianu

Graniastosłup

Graniastosłup to bryła, której wszystkie ściany boczne są prostokątami, a obie podstawy są przystające i równoległe do siebie.

• Każda krawędź boczna jest prostopadła do podstaw. Jej długość nazywamy wysokością graniastosłupa.
• Graniastosłup przyjmuje swoją nazwę od wielokąta, który jest jego podstawą.

Objętość graniastosłupa jest równa iloczynowi jego pola podstawy i wysokości.

V = Pp • h

Pp – pole podstawy
h – wysokość

Pole powierzchni całkowitej graniastosłupa jest sumą pól wszystkich jego ścian.

Pc= 2 • Pp + Pb

Pc – pole powierzchni całkowitej
Pp – pole podstawy
Pb – pole powierzchni bocznej (suma pól wszystkich ścian bocznych

Ostrosłup

Ostrosłup to bryła, której podstawa jest dowolnym wielokątem, a ściany boczne są trójkątami o wspólnym wierzchołku, który nosi nazwę wierzchołka ostrosłupa. Ostrosłup, tak jak graniastosłup, przyjmuje swoją nazwę od wielokąta, który jest jego podstawą, np.:

Czworościan to ostrosłup trójkątny.

Czworościan foremny to czworościan, którego wszystkie ściany są trójkątami równobocznymi.

Ostrosłup prawidłowy to taki, w którym:

• ściany boczne są przystającymi trójkątami równoramiennymi
• podstawa jest wielokątem foremnym.

Objętość ostrosłupa

Pp – pole podstawy
h – wysokość

Pole powierzchni całkowitej ostrosłupa to suma pola podstawy i pola powierzchni bocznej ostrosłupa.

Pc = Pp + Pb

Pc – pole powierzchni całkowitej
Pp – pole podstawy
Pb – pole powierzchni bocznej (suma pół wszystkich ścian bocznych)