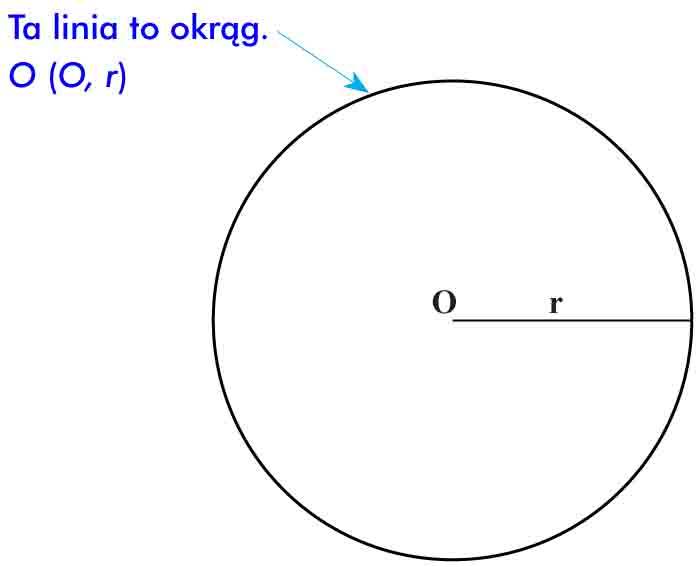
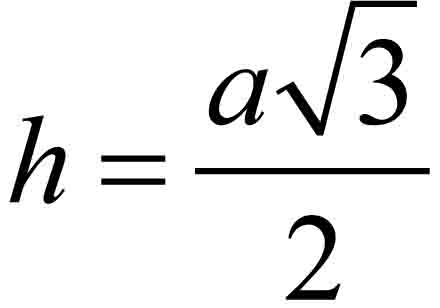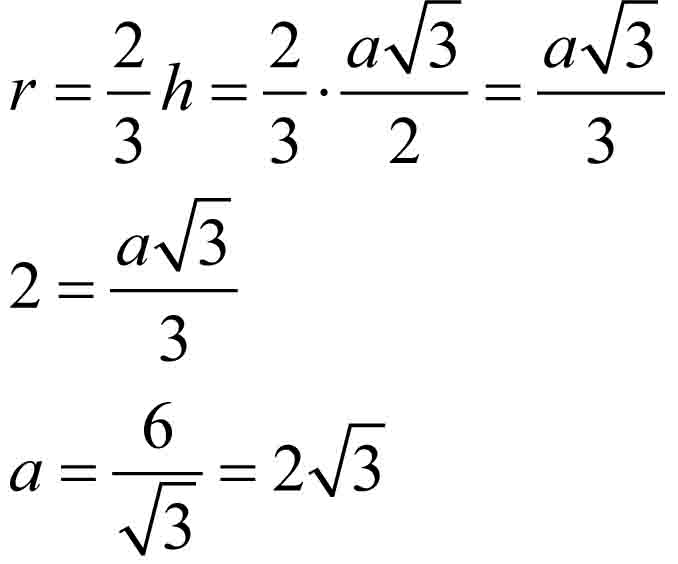Okręgiem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O wynosi r.
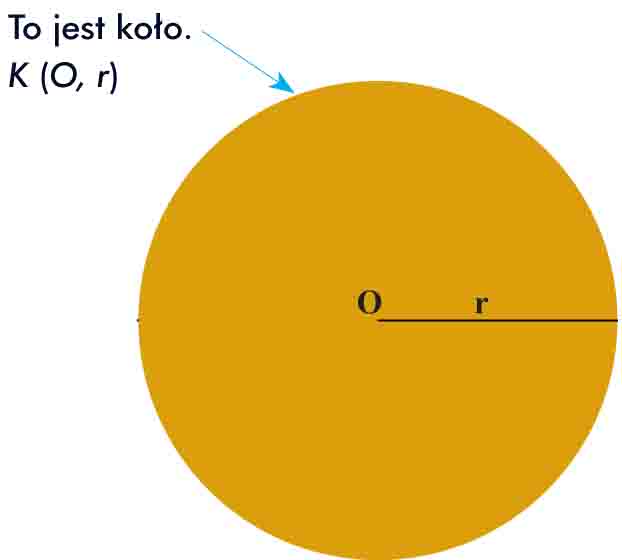
Kołem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O jest mniejsza lub równa r.
Zauważ!
Środek okręgu nie należy do okręgu, środek koła należy do koła.
To jest ważne!
W okręgu i kole można zaznaczyć:
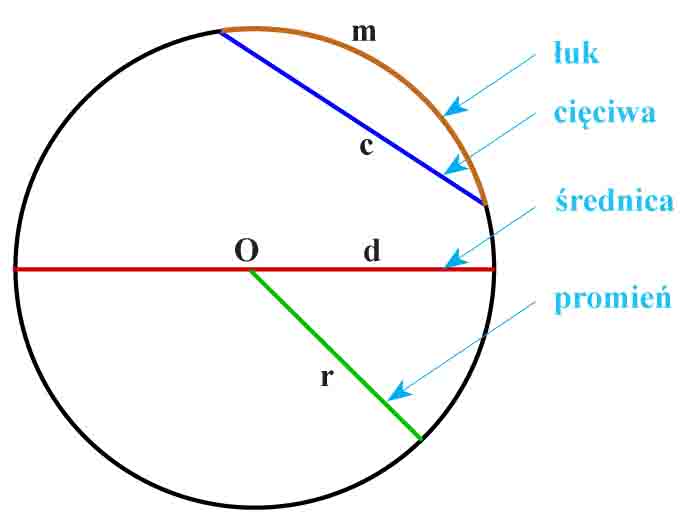
- Promień r – odcinek, którego jednym końcem jest środek okręgu O, a drugi koniec leży na okręgu.
- Cięciwę c – odcinek, którego oba końce leżą na okręgu.
- Średnicę d – cięciwę przechodzącą przez środek okręgu O.
- Łuk m – część okręgu zawartą między dwoma różnymi punktami okręgu wraz z tymi punktami.
Nie myl tych pojęć!
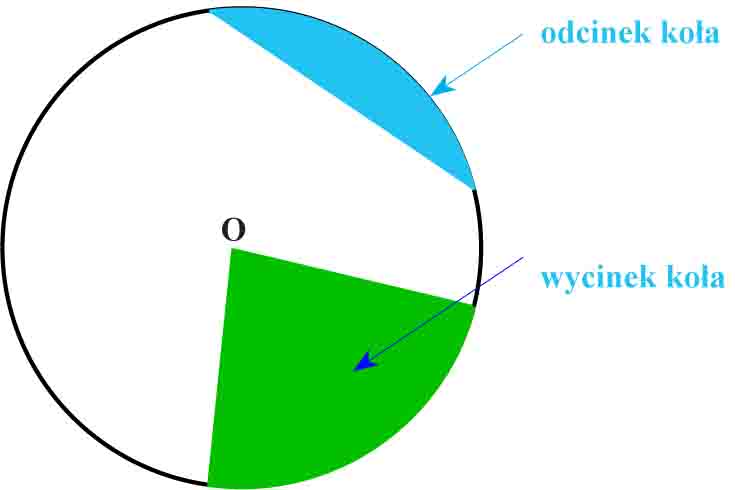
Cięciwa dzieli koło na dwie części. Każdą z tych części nazywamy odcinkiem koła.
Wycinek koła jest częścią powierzchni koła ograniczoną łukiem i dwoma promieniami.
Zadanie 1
Rysunek przedstawia ślad na śniegu, który zostawił jadący na nartach Adam.
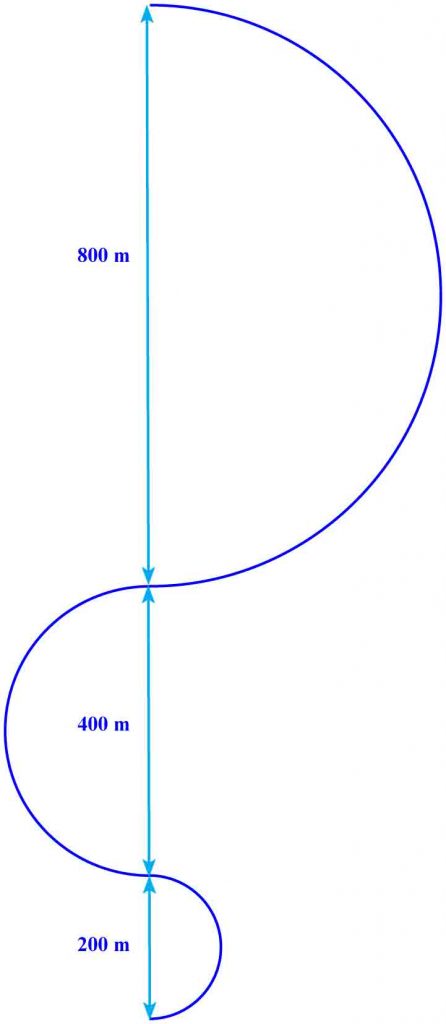
Długość trasy przebytej przez Adama równa jest:
A. 350 π m
B. 700 π m
C. 1400 π m
D. 2100 π m
Powtórz!
Obwód koła: L = 2πr; L = πd
r – promień
d – średnica
Rozwiązanie:
Długość trasy przebytej przez Adama obliczysz, korzystając ze wzoru na obwód koła L = π • d.
L = 1/2 · π (800 + 400 + 200) = 700 π [m]
Uwaga! 1/2 ponieważ Adam pokonuje trasę połowy okręgu.
Odpowiedź: B.
Zadanie 2.
W rozpadlinie skalnej powstało jeziorko, którego powierzchnia ma kształt koła o średnicy 20 m. Oblicz pole powierzchni tego koła. Podaj dokładny wynik.
Rozwiązanie:
Ponieważ średnica ma długość 20 m, to długość promienia wynosi 10 m. Po podstawieniu do wzoru ![]() obliczasz pole powierzchni jeziorka:
obliczasz pole powierzchni jeziorka: ![]()
Odpowiedź:
Pole powierzchni jeziorka wynosi 100π [m2].
Zadanie 3.
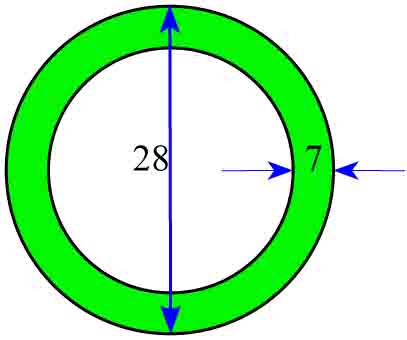
Na miejscu dawnego skrzyżowania postanowiono wybudować rondo, którego wymiary (w metrach) podane są na rysunku. Oblicz, na jakiej powierzchni trzeba wylać asfalt (obszar zacieniowany na rysunku).
W swoich obliczeniach za π podstaw 22/7.
Powtórz!
Pierścień kołowy – zbiór punktów ograniczony dwoma współśrodkowymi okręgami.
Pierścień kołowy jest więc różnicą dwu współśrodkowych kół z dołączonym okręgiem mniejszego koła.
Rozwiązanie:
Pole pierścienia kołowego liczymy jako różnicę pól dwu współśrodkowych kół.
Długości promieni tych kół wynoszą: r = (28 − 8) : 2 =10 m, R = 14 m.
Pola kół wynoszą zatem:
![]()
Pole pierścienia jest więc równe:
(π⋅196) − (π⋅100) = (π⋅96) m²
Zadanie 4.
Tata planuje wykonanie klombu w kształcie koła o promieniu 2 m. Białymi krokusami zamierza obsadzić obrzeże klombu, a żółtymi – boki trójkąta równobocznego, wpisanego w to koło, bez jego wierzchołków. Ile będzie potrzebował cebulek białych krokusów, a ile żółtych, jeżeli sadzi się je w odstępach około 10 cm? Przyjmij, że π » 3,14, √3 » 1,7.
Rozwiązanie:
Obliczasz najpierw obwód koła o promieniu 2m:
L = 2 · π · 2 = 4 · 3,14 = 12,56 [m]
Ponieważ krokusy mają być sadzone w odstępach około 10 cm (0,1 m), więc wyliczasz liczbę białych krokusów:
12,56 : 0,1 = 126
Zauważ, że promień koła stanowi 2/3 wysokości trójkąta równobocznego (r = 2/3 h).
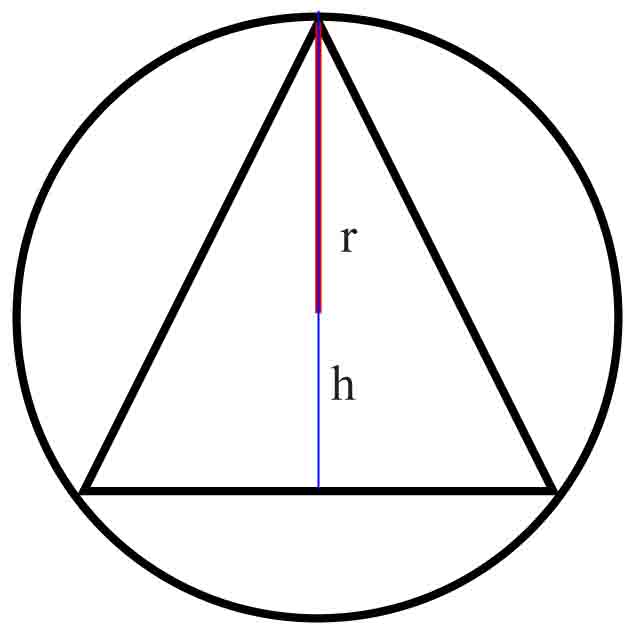
Korzystając ze wzoru na wysokość w trójkącie równobocznym, obliczasz długość boku tego trójkąta.
Wzór na wysokość w trójkącie równobocznym
Obwód trójkąta równobocznego wynosi zatem:
L = 3a
L = 6 √3 ≈ 10,2 [m]
Teraz możesz obliczyć liczbę żółtych krokusów, uwzględniając to, że w wierzchołkach trójkąta posadzono krokusy białe:
10,2 : 0,1 – 3 ≈ 102 – 3 ≈ 99
Odpowiedź: Potrzeba 126 krokusów białych i 99 krokusów żółtych.
Powtórz!
Okrąg jest opisany na wielokącie, jeżeli wszystkie wierzchołki tego wielokąta leżą na okręgu.
Czy wiesz, że…
Czworokąt można wpisać w okrąg, jeżeli sumy przeciwległych kątów są sobie równe i wynoszą 180°.
a + b = g + d
Czworokąt można opisać na okręgu, jeżeli sumy przeciwległych boków są sobie równe.
a + c = b + d
Okrąg jest wpisany w wielokąt, jeżeli jest styczny do wszystkich boków tego wielokąta.
Poćwicz
1. Ile stopni ma kąt środkowy oparty na 5/6 okręgu?
2. Ile stopni ma kąt wpisany oparty na 5/6 okręgu?
3. Pole największego koła, które można wyciąć z kwadratu o polu 100 m², wynosi:
A. 100 π m²
B. 10 π m²
C. 20 π m²
D. 25 π m²
4. Podczas spaceru brat Zosi jedzie czterokołowym rowerkiem. Obwód dużego koła wynosi 80 cm, a małego 40 cm. O ile obrotów więcej wykona małe koło rowerka niż duże na półkilometrowym odcinku drogi?
A. 2500
B. 1250
C. 625
D. 400
5. Na lekcji jazdy konnej dzieci dosiadały konia prowadzonego po okręgu na napiętej uwięzi o długości 5 m. Jaką drogę pokonał koń, jeżeli łącznie przebył 40 okrążeń? Wynik zaokrąglij do 0,1 km.
A. Około 1,3 km
B. Około 1 km
6. (egzamin próbny OKE Kraków 2004)
Obwód pnia jednego z dębów na pewnej wysokości nad ziemią wynosi 7,85 m. Promień przekroju pnia na tej wysokości ma długość około:
A. 100 cm
B. 125 cm
C. Około 0,2 km
D. Około 12,6 km
Odpowiedzi
1. 5/6 · 360° = 300°;
2. 1/2 · ( 5/6 · 360°) = 150°;
3. D.;
4. C.;
5. A.;
6. B.