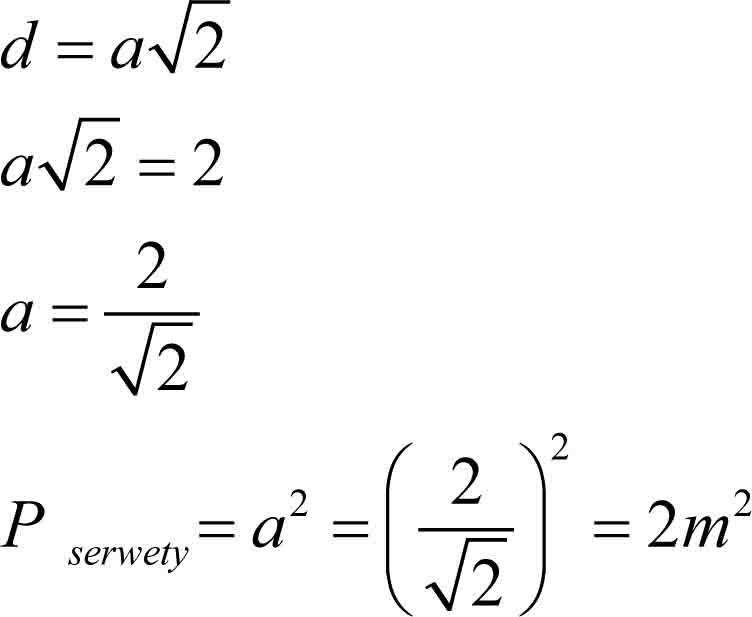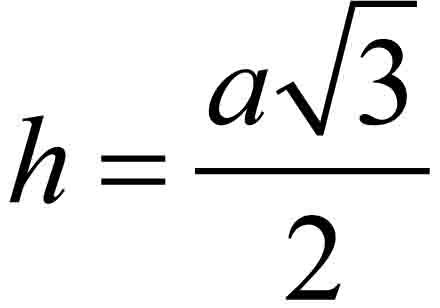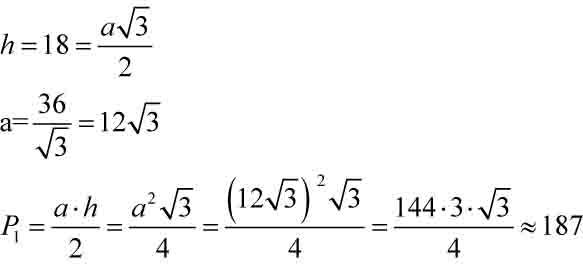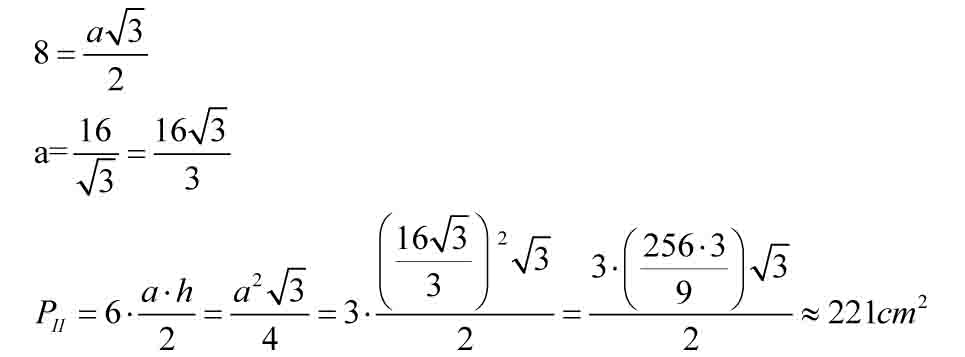Musisz wiedzieć!
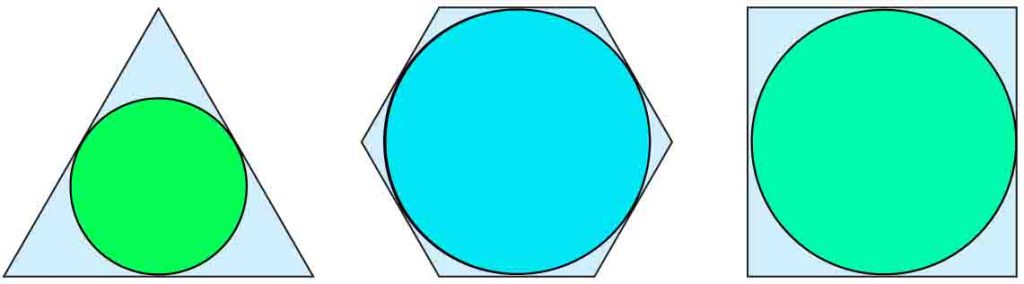
- Okrąg jest wpisany w wielokąt, jeżeli jest styczny do wszystkich boków tego wielokąta.
- Okrąg jest opisany na wielokącie, jeżeli wszystkie wierzchołki wielokąta leżą na okręgu.
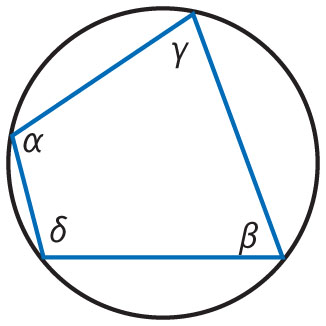
Wielokąt wpisany w okrąg
Okrąg opisany na wielokącie
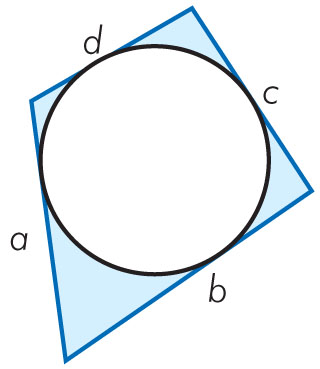
Wielokąt opisany na okręgu
Okrąg wpisany w wielokąt
Zadanie 1.
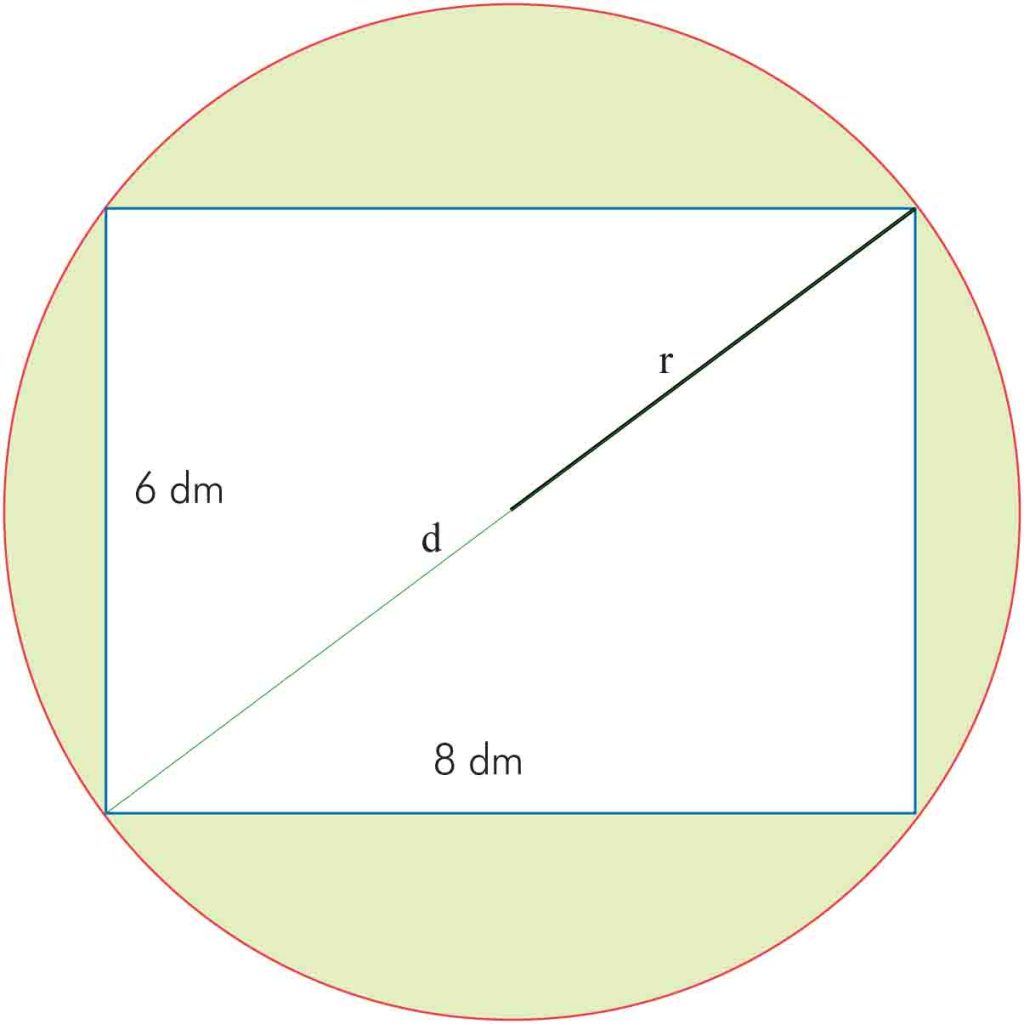
Drewniany blat stołu w kształcie koła przerobiono na prostokątny. Długości boków otrzymanego prostokąta wynoszą 6 dm i 8 dm. Oblicz pole powierzchni pozostałej części blatu (obszar zacieniowany).
Rozwiązanie:
Chcąc obliczyć pole zacieniowanego obszaru, musimy od pola koła odjąć pole prostokąta.
Korzystając z twierdzenia Pitagorasa, wyliczmy długość przekątnej prostokąta, która jest jednocześnie średnicą koła:
d² = 6² + 8² czyli d = 10 dm oraz r = 5 dm.
Pole koła wynosi więc Pk = π · 5² = 25π [dm²], a pole prostokąta Pp = 48 [dm²]. Szukane pole to różnica 25π – 48 [dm²].
Odpowiedź: Pole powierzchni pozostałej części blatu wynosi 25π – 48 [dm²].
Zadanie 2.
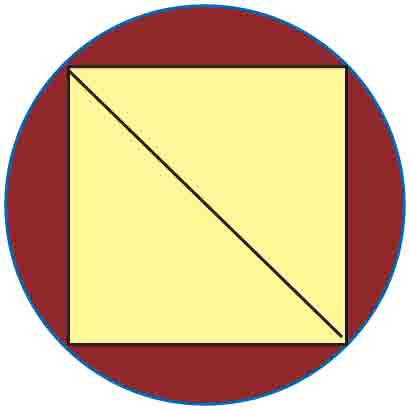
Blat stołu ma kształt koła o obwodzie 2π m. Na stole położono kwadratową serwetę, której przekątna jest równa średnicy blatu stołu. Jaką częścią powierzchni całego stołu jest powierzchnia zajmowana przez serwetę? Przyjmij, że π ≈ 3.
Rozwiązanie:
Korzystając ze wzoru na obwód koła, wyliczymy najpierw długość promienia blatu:
2πr = 2π
r = 1 [m]
Pole powierzchni blatu wynosi zatem Pblatu = π · 1² ≈ 3 [m²]. Ponieważ przekątna serwety ma długość równą średnicy blatu (2 m), więc długość jej boku po wykorzystaniu wzoru na przekątną w kwadracie wynosi
Ostatecznie otrzymujemy
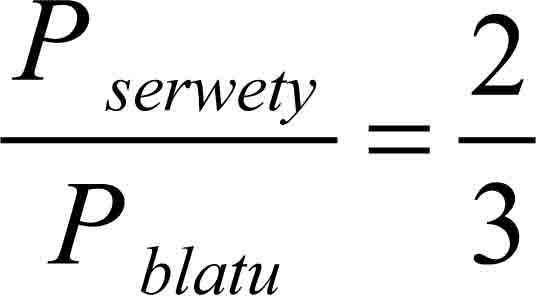
Odpowiedź: Serweta zajmuje 2/3 powierzchni całego stołu.
Zadanie 3.
W pewnej drużynie harcerskiej każdy z trzech zastępów postanowił wykonać swój proporczyk. Proporczyki te miały mieć kształty wielokątów foremnych z naszytym w środku kołem wpisanym w ten wielokąt. Który z zastępów zużył najmniej, a który najwięcej materiału na wykonanie swojego proporczyka? Przyjmij √3 ≈ 1,73.
ZASTĘP I ZASTĘP II ZASTĘP III
Średnica koła Średnica koła Średnica koła
d = 12 cm d = 16 cm d = 14 cm
Rozwiązanie:
Musimy kolejno obliczać pola powierzchni każdego z proporczyków.
ZASTĘP I
Proporczyk ma kształt trójkąta równobocznego. Skoro d = 12 cm, to promień okręgu wpisanego wynosi 6 cm. Ponieważ długość promienia okręgu wpisanego stanowi 1/3 wysokości trójkąta równobocznego, więc wysokość trójkąta wynosi 18 cm (r = 1/3 h, czyli h = 3r). Teraz korzystamy ze wzoru na wysokość w trójkącie równobocznym i obliczamy długość boku trójkąta:
ZASTĘP III
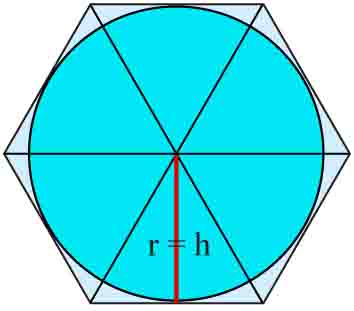
Ten zastęp ma proporczyk w kształcie sześciokąta foremnego. Promień koła wpisanego w ten wielokąt wynosi 8 cm. Długość tego promienia jest równa wysokości każdego z trójkątów równobocznych, z których składa się ten sześciokąt
Obliczamy teraz długość boku sześciokąta:
ZASTĘP II
Obliczenia dla trzeciego zastępu są najprostsze, bo skoro
r = 7 cm, a r = 1/2 a, to a = 14 cm. Pole proporczyka będącego kwadratem wynosi więc PIII = 142 = 196 [cm²].
Wnioski: PI < PIII < PII
Odpowiedź: Najmniej materiału zużył zastęp pierwszy, a najwięcej zastęp drugi.
Zadanie 4.
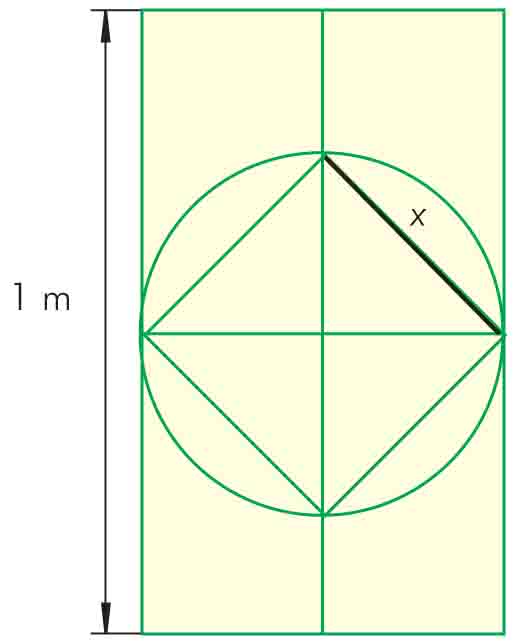
Rysunek przedstawia fragment płotu. Ile metrów drutu zużyto na wykonanie takiego jednego elementu, jeżeli długość zaznaczonego odcinka wynosi x = 25√2 cm, a wysokość płotu jest równa 1 metr? Przyjmij √2 ≈1,41 oraz π ≈ 3,14.
Rozwiązanie:
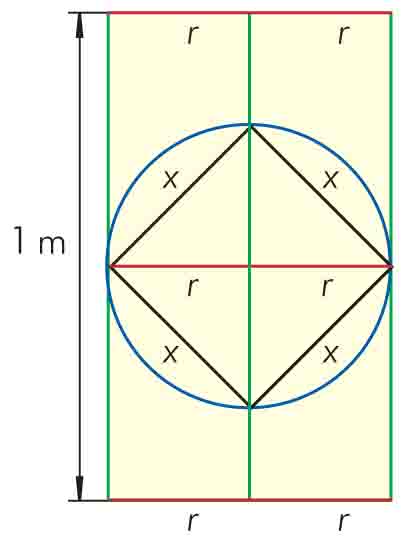
Warto przyjrzeć się dobrze rysunkowi i wprowadzić na nim dodatkowe oznaczenia literowe oraz zaznaczyć tym samym kolorem odcinki o jednakowej długości.
Ustalimy najpierw, ile wynosi długość odcinka r, który jest promieniem koła (zaznaczonego kolorem niebieskim). Ponieważ odcinek składający się z dwóch promieni jest jednocześnie przekątną kwadratu (zaznaczonego kolorem czarnym), więc po wykorzystaniu wzoru na przekątną kwadratu mamy, że 2r = x√2, 2r = 25√2 · √2, 2r = 50, czyli ostatecznie
r = 25 cm. Teraz wystarczy stwierdzić, że na ilość zużytego drutu składać się będą 3 odcinki zielone, 6 odcinków czerwonych, 4 odcinki czarne i długość niebieskiego okręgu:
3 · 100 + 6 · 25 + 4 · 25√2 + 2π · 25 ≈ 450 + 100 · 1,41 + 50 · 3,14 ≈ 748 [cm]
Odpowiedź: Na wykonanie fragmentu płotu zużyto około 748 cm drutu.