Prosta, płaszczyzna, punkt, odcinek, łamana, kąt, rodzaje kątów
W geometrii istnieją pojęcia PIERWOTNE, których definicji nie jesteśmy w stanie podać. Do takich pojęć należy: PUNKT, PROSTA, PŁASZCZYZNA.Wszystkie inne pojęcia są pochodnymi pierwotnych i dzięki nim definiowane.
PUNKT oznaczamy dużymi literami alfabetu, np.: • A • B • C
PROSTE oznaczamy małymi literami alfabetu np. : p
Prosta jest to linia, która nie ma ani początku ani końca.
Punkt leżący na prostej dzieli tę prostą na dwie PÓŁPROSTE, np. :
Półprosta jest ograniczona z jednej strony przez punkt, który nazywa się początkiem półprostej. Z drugiej strony półprosta nie jest ograniczona. Długość półprostej jest nieskończona.
Dwa różne punkty A i B na prostej wyznaczają ODCINEK AB.
Odcinek ograniczony jest z obu stron przez punkty A i B, które nazywamy koñcami odcinka.
Uwaga!
Odcinki można dodawać i odejmować.
Długość odcinka AB oznaczamy symbolem |AB|
Zadanie 1
Dane są dwa odcinki różnej długości a i b, takie, że a>b.
Wyznacz geometrycznie ich sumę i różnicę.
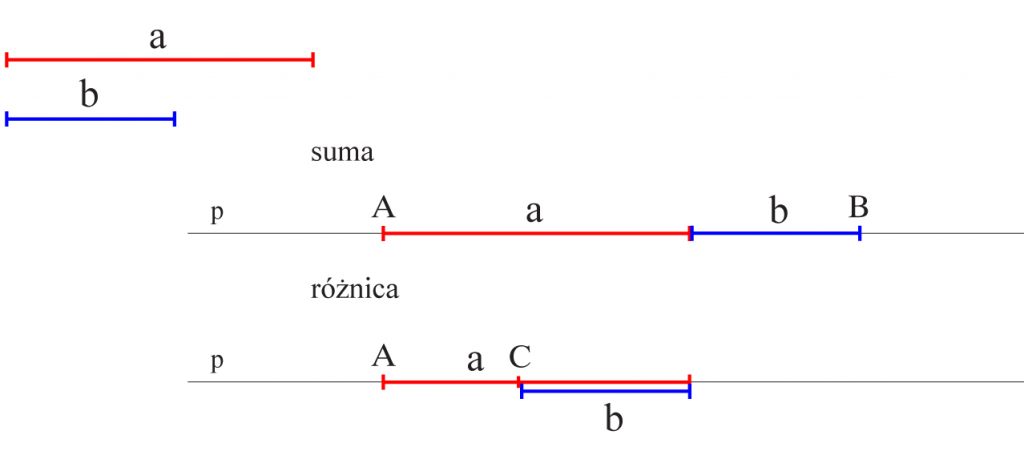
Rozwiązanie:
AB = a + b
AC = a – b
Zadanie 2
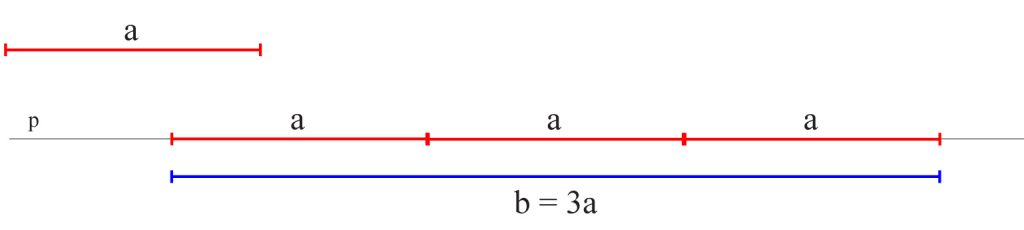
Mając dany odcinek a, nakreśl odcinek b = 3a
Rozwiązanie: b = 3a
Zadanie 3
Są cztery takie odcinki, że długość pierwszego wynosi 3 cm, a długość każdego następnego odcinka jest dwa razy większa od poprzedniego. Ile cm długości ma suma tych czterech odcinków?
Rozwiązanie:
a = 3 cm
b = 2 . 3 cm = 6 cm
c = 2 . 6 cm = 12 cm
d = 2 . 12 cm = 24 cm
a + b + c + d = 3 + 6 + 12 + 24 = 45 (cm)
Odp: Suma długości odcinków wynosi 45 cm.
Zadanie 4
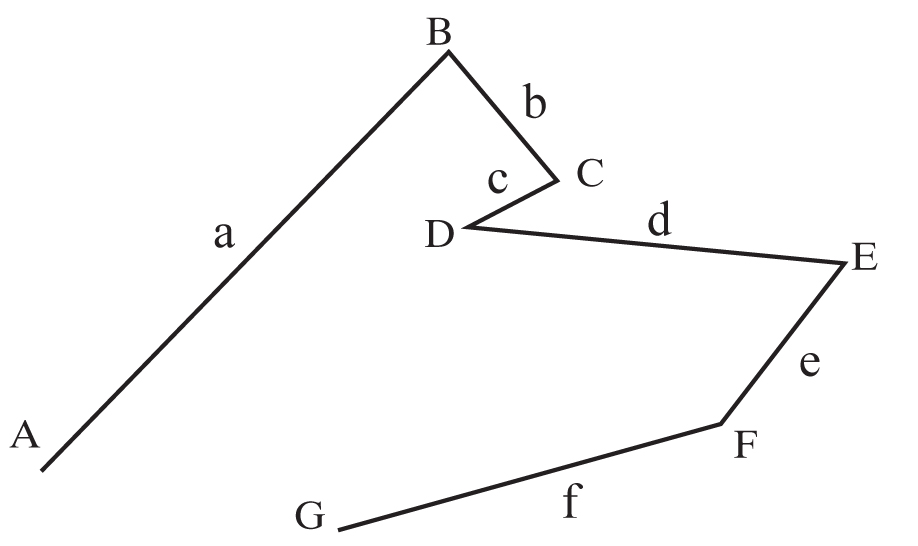
Dane są odcinki a, b, c, d, e, f. Ułóżmy je tak, że koniec jednego odcinka jest równocześnie początkiem następnego i żadne dwa kolejne odcinki nie leżą na jednej prostej.
Otrzymaliśmy ŁAMANĄ
Odcinki a, b, c, d, e, f nazywamy BOKAMI łamanej. Końce odcinków czyli punkty A, B, C, D, E, F, G nazywamy WIERZCHOŁKAMI łamanej. Łamana przedstawiona na powyższym rysunku jest OTWARTA.
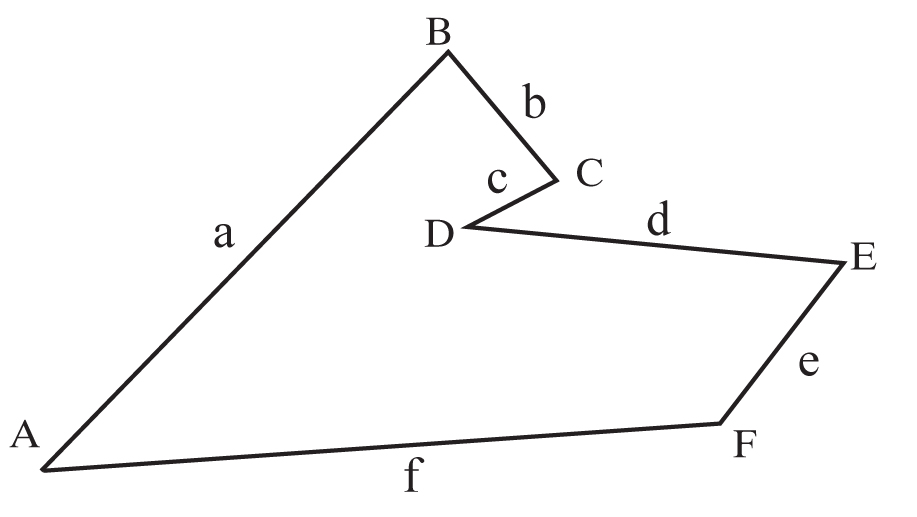
Jeśli punkty A i G pokryłyby się, łamana byłaby ZAMKNIĘTA. np.:
Jeśli boki łamanej mają wspólne punkty oprócz wierzchołków, łamana nazywa się WIĄZANA, w przeciwieństwie do ZWYKŁEJ przedstawionej wcześniej.
WIĄZANA OTWARTA WIĄZANA ZAMKNIĘTA
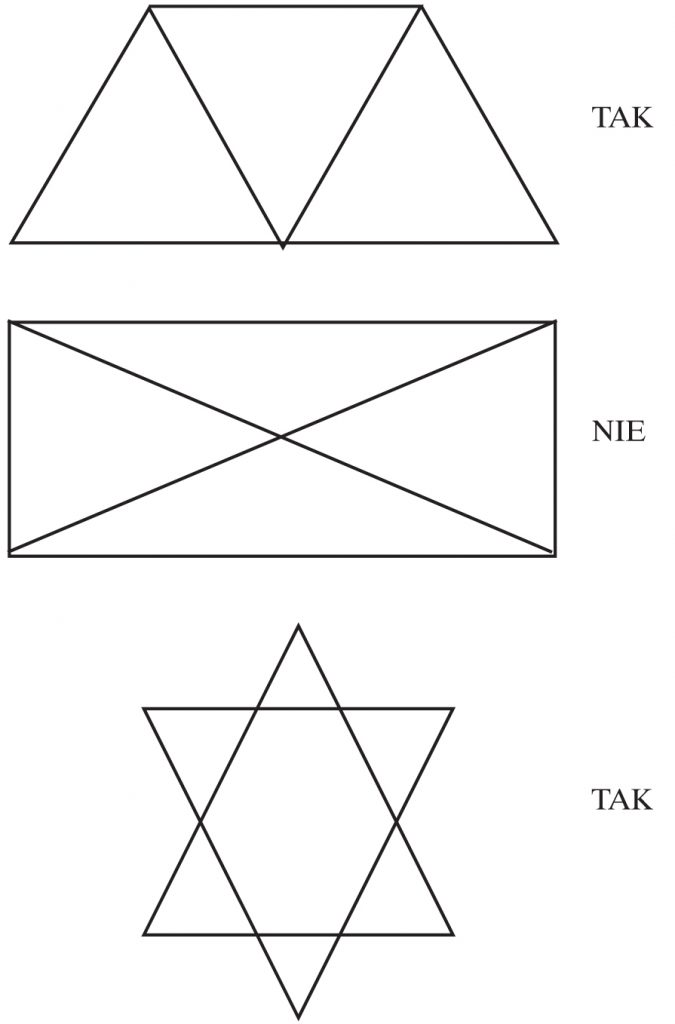
Uwaga 2) Łamaną można narysować jednym ciągiem, nie odrywając ołówka od papieru i nie prowadząc go powtórnie po żadnym boku.
Zadanie 5
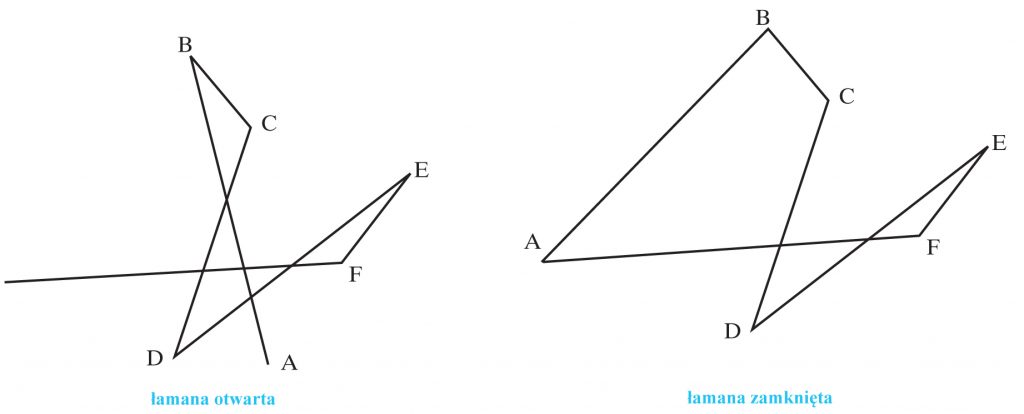
Czy poniższe figury są łamanymi?
Dlaczego? Skorzystaj z uwagi 2)
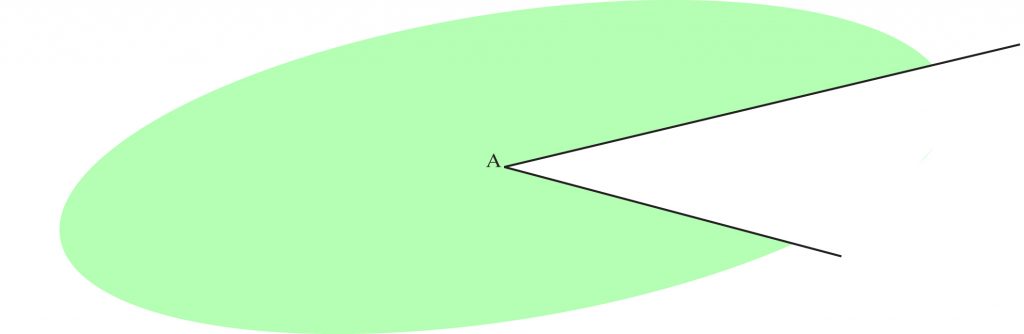
Narysujmy na płaszczyźnie dwie różne półproste o wspólnym początku, nie należące do jednej prostej. Płaszczyzna została podzielona w ten sposób na dwa obszary, z których każdy nazywamy kątem.
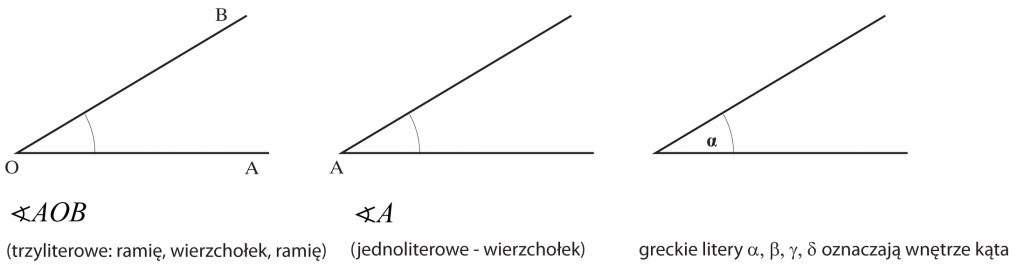
Wspólny początek półprostych nazywamy WIERZCHOŁKIEM kąta, a owe półproste – jego RAMIONAMI.
Oznaczenia:
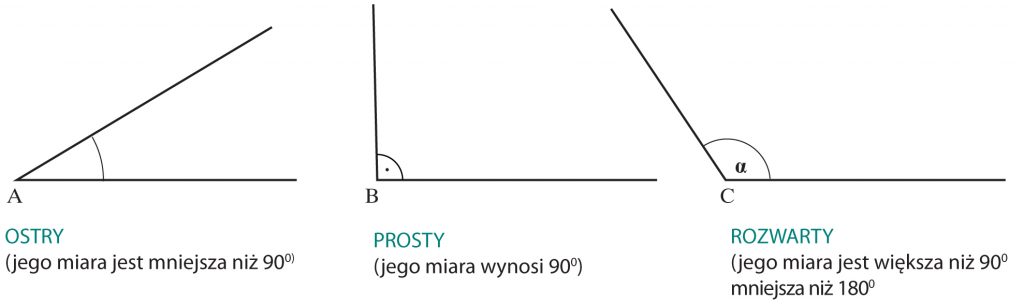
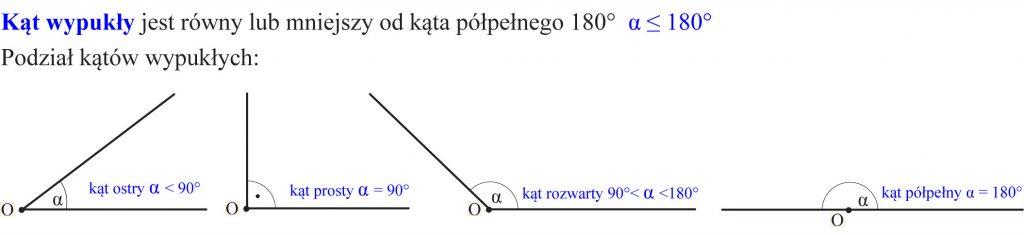
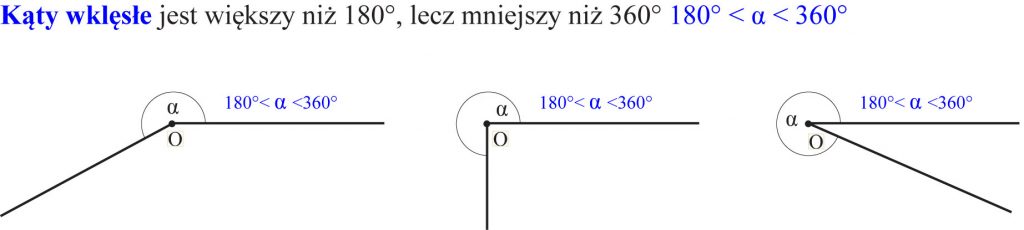
Rodzaje kątów:
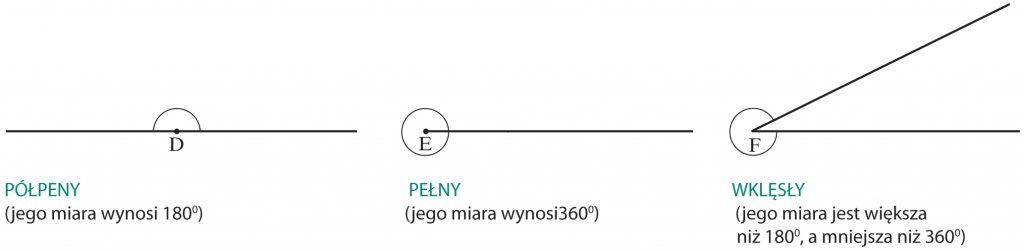
KĄTY: PÓŁPEŁNY, PEŁNY, WYPUKŁY, WKLĘSŁY
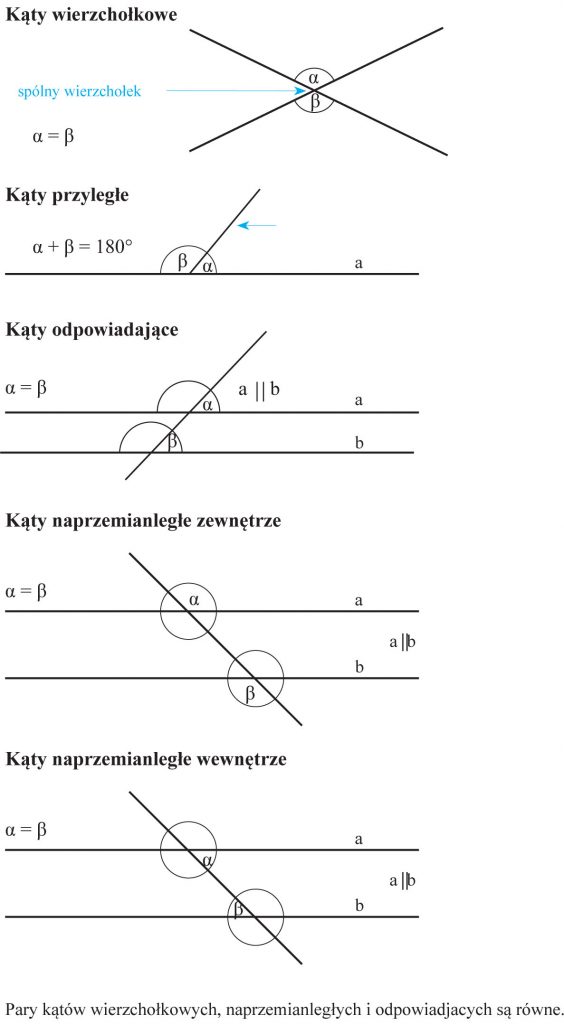
Przy rozwiązywaniu zadań potrzebna też będzie znajomość kątów:
Zadanie 6
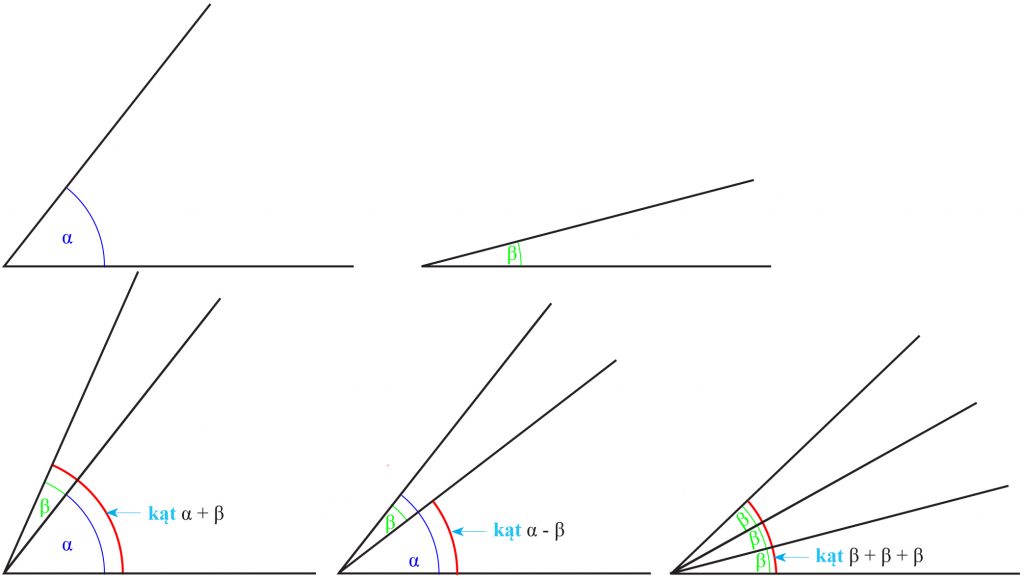
Dane są dwa kąty α i β takie, że α> β Nakreśl kąt
a) α + β;
b) α − β;
c) 3β
Rozwiązanie:
Okazuje się, że kąty można dodawać lub odejmować.
Zadanie 8
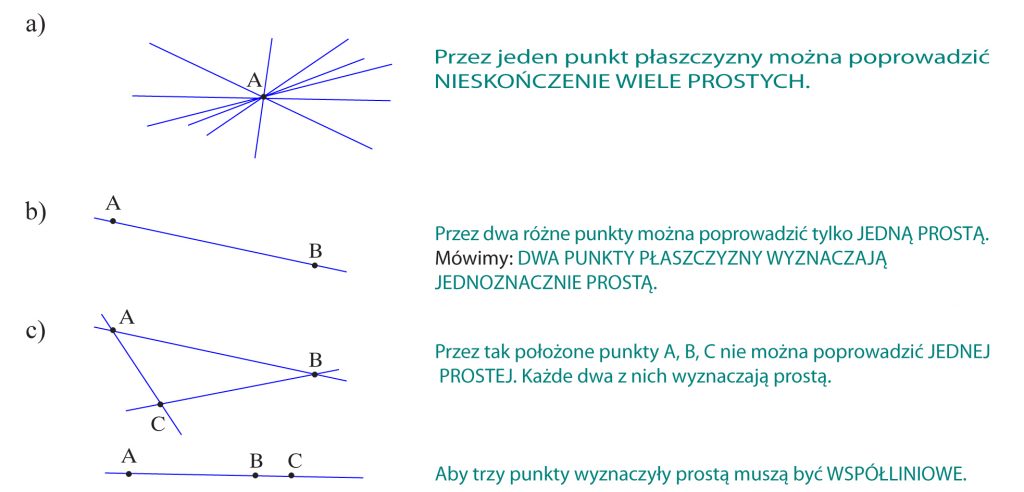
Ile różnych prostych można poprowadzić, przez:
a) jeden punkt płaszczyzny
b) dwa różne punkty płaszczyzny
c) trzy różne punkty płaszczyzny
Zastanówmy się teraz, jak mogą być położone względem siebie, dwie proste na płaszczyźnie.
Otóż, mogą:
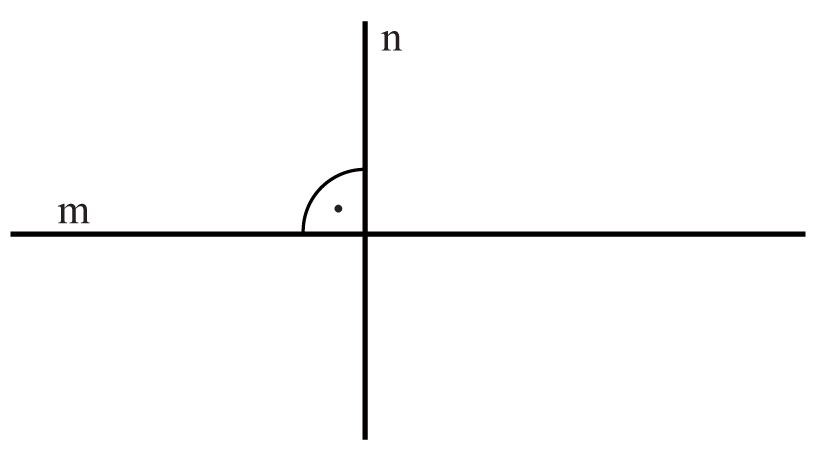
Jeżeli proste przecinają się, tworząc ze sobą kąty proste, nazywamy je PROSTYMI PROSTOPADŁYMI.
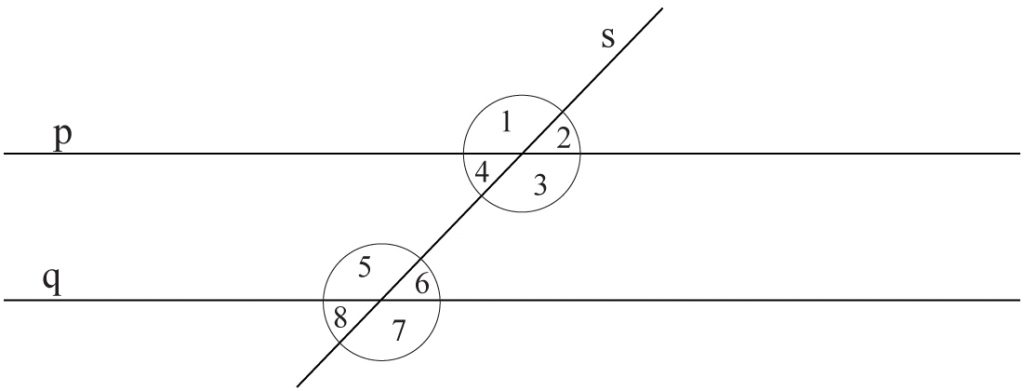
Dwie proste równoległe, które przecięte zostały trzecią prostą (sieczną) tworzą 8 kątów. (a||b)
Kąty wierzchołkowe (są równe parami)
kąt 1 i kąt 3
kąt 2 i kąt 4
kąt 5 i kąt 7
kąt 6 i kąt 8
Kąty przyległe (ich suma jest równa kątowi półpełnemu)
kąt 1 i kąt 2
kąt 1 i kąt 4
kąt 2 i kąt 3
kąt 3 i kąt 4
kąt 5 i kąt 6
kąt 6 i kąt 7
kąt 7 i kąt 8
kąt 5 i kąt 8
Kąty odpowiadające (są równe parami)
kąt 1 i kąt 5
kąt 2 i kąt 6
kąt 4 i kąt 8
kąt 3 i kąt 7
Kąty naprzemianległe zewnętrzne (są równe Kąty odpowiadające (są równe parami)
ąt 1 i kąt 7
kąt 2 i kąt 8
Kąty naprzemianległe wewnętrzne (są równe parami)
kąt 4 i kąt 6
kąt 3 i kąt 5
Równość kątów odpowiadających lub naprzemianległych przy dwóch prostych p i q przeciętych sieczną s jest znakiem rozpoznawczym równoległości prostych p i q.
Zadanie 9
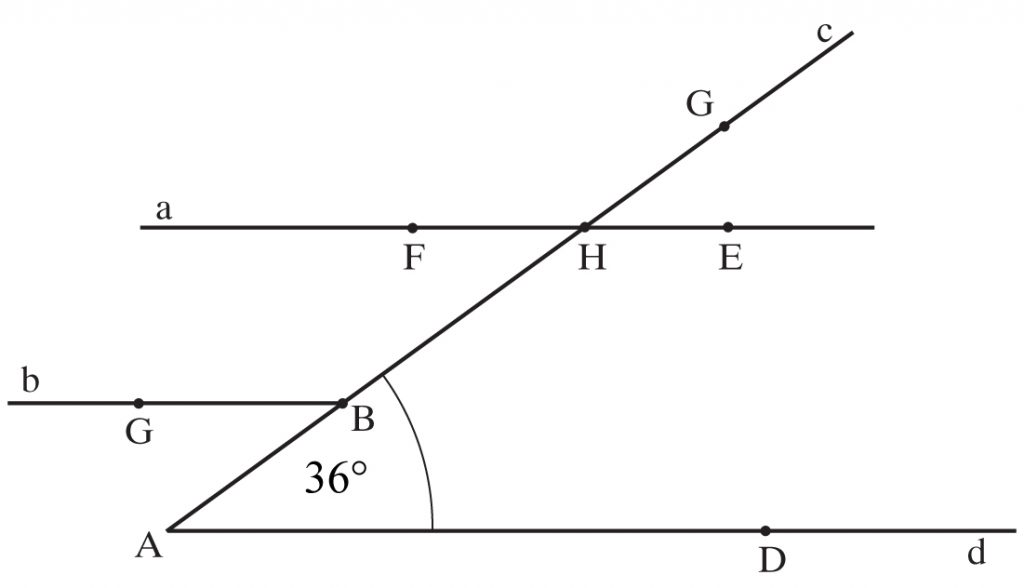
Oblicz kąty danej figury, wiedząc, że kąt BAD = 36°, a || b || d.
Kąt GHE = kąt BAD = 36° jako odpowiadające
Kąt BHF = kąt BAD = 36° jako naprzemianległe wewnętrzne
Kąt FHB = kąt GBA = 36° jako odpowiadające
Kąt GHF = 180° – 36° = 144° jako przyległy do kąta GHE
Kąt GBH = kąt FHG = 144° jako odpowiadające.
Zadanie 10
Obliczyć długość łamanej, o podanych długościach boków:
|AB| = 2,8 cm
|BC| = 2,8 cm
|CD| = 3,5 cm
|DE| = 5,1 cm
|EF| = 2,6 cm
długość łamanej wynosi:
|AB| + |BC| + |CD| + |DE| + |EF| = 2,8 cm + 2,8 cm + 3,5 cm + 5,1 cm + 2,6 cm = 16,8 cm