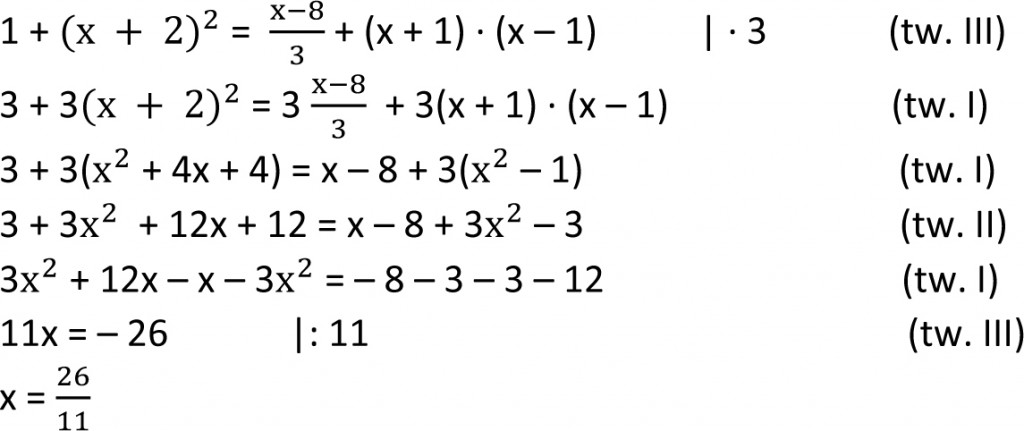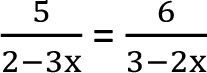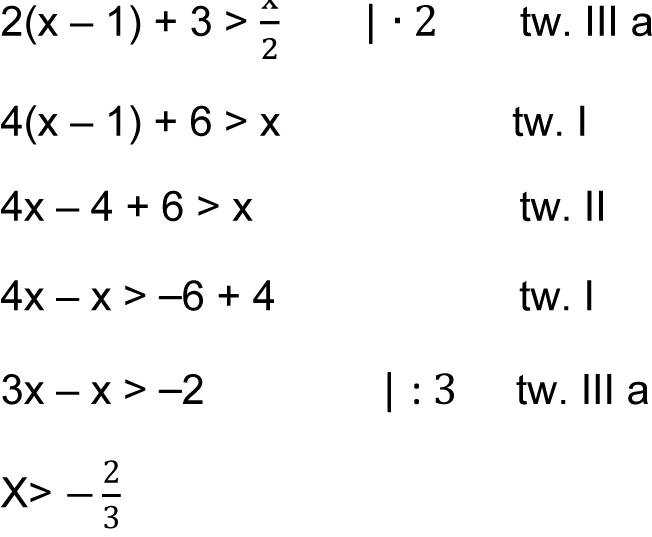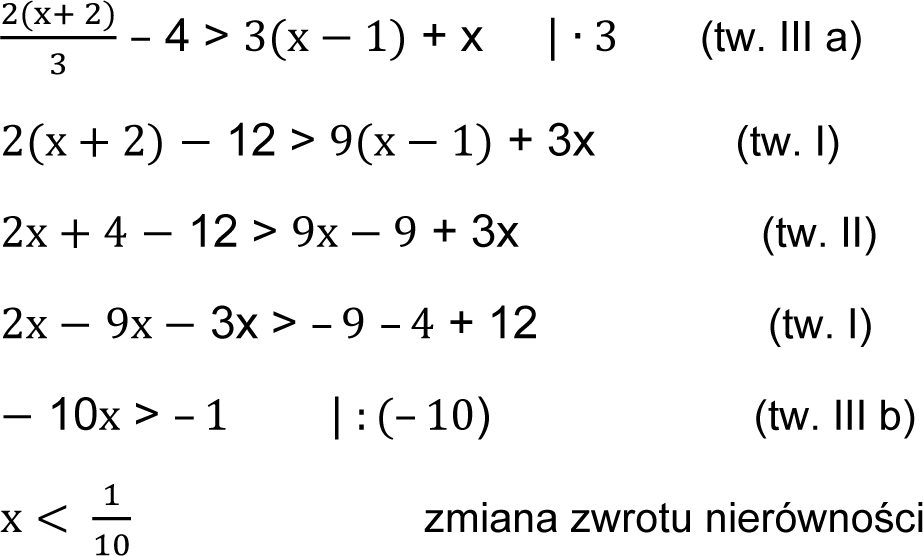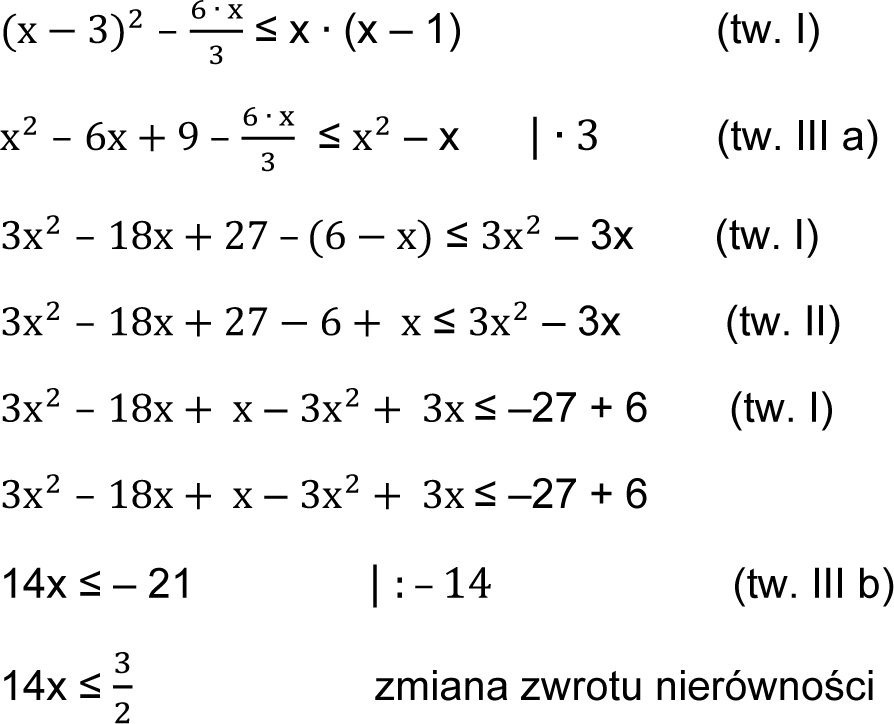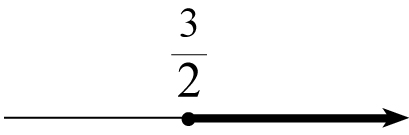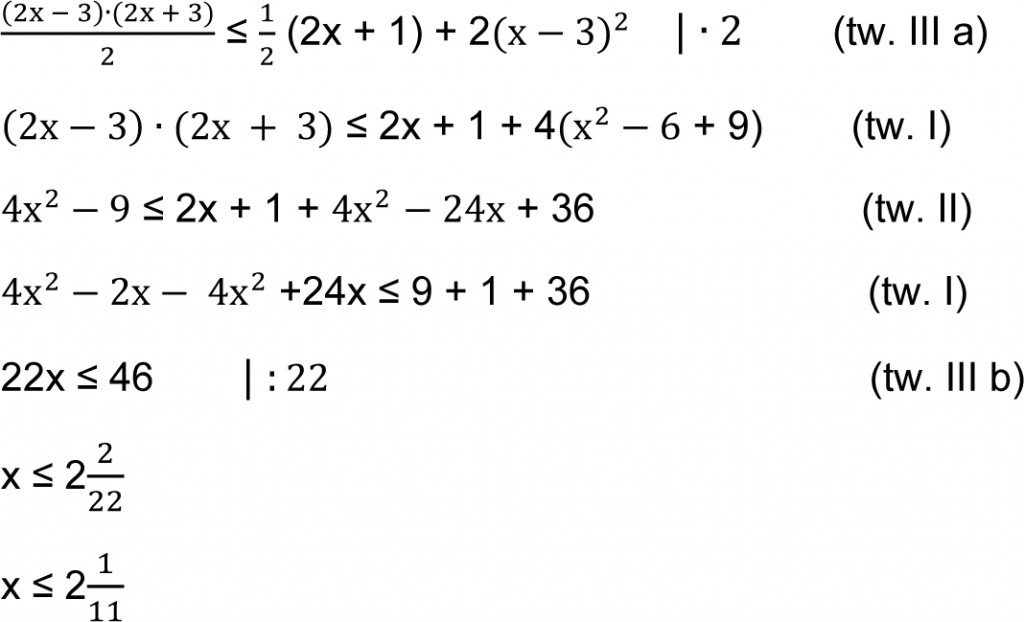Równania i nierówności pierwszego stopnia z jedną niewiadomą

Równania

Równaniem nazywamy równość dwóch wyrażeń, z których przynajmniej jedno jest algebraiczne.

Równania, w których występuje tylko jedna zmienna literowa, czyli niewiadoma w pierwszej potędze, nazywamy równaniem pierwszego stopnia z jedną niewiadomą.
Rozwiązać równanie, to znaczy znaleźć taką liczbę, która podstawiona do równania w miejsce niewiadomej spełnia (sprawdza) to równanie. Taką liczbę nazywamy pierwiastkiem równania.

Np.:
równanie x + 1 = 3 ma pierwiastek 2 i tylko ten pierwiastek;
a równanie 5x = 10 ma też jeden pierwiastek 2.
Mówimy, że równania: x + 1 = 3 i 5x = 10 są równoważne.

Zapamiętaj!
Równania, które mają te same pierwiastki nazywamy równaniami równoważnymi.

Rozwiążmy równanie:

I. 3(2x – 1) – 5(x – 3) + 6(3x – 4) = 83 ––– usuwamy nawiasy

II. 6x – 3 – 5x + 15 + 18x – 24 = 83 —–– przenosimy wiadome na prawą stronę równania

III. 6x – 5x + 18x = 83 + 3 – 15 + 24 —– redukujemy wyrazy podobne

IV. 19x = 95 ——— dzielimy obie strony równania przez 19

V. x = 5

Liczba 5 jest jedynym rozwiązaniem (pierwiastkiem) równania I, II, III, IV, i V.
Sprawdzić to można podstawiając zamiast x liczbę 5 i badając prawdziwość znaku równości, w każdym powyższym równaniu, czyli I, II, III, IV, i V.
A zatem są to równania równoważne.

Przekształcając równanie na równanie równoważne stosujemy następujące twierdzenia.

Twierdzenie I
Jeśli jedną lub obydwie strony równania przekształcimy tożsamościowo, to otrzymamy równanie równoważne danemu.

Uwaga! Przekształcenie tożsamościowe to:

stosowanie praw działań
redukcja wyrazów podobnych
usunięcie nawiasów
stosowanie wzorów skróconego mnożenia, itp.

Twierdzenie II
Jeśli do obu stron równania, dodamy lub odejmiemy to samo wyrażenie, to otrzymamy równanie równoważne danemu.
Uwaga! Oznacza to w praktyce, że z jednej strony równania na drugą można przenosić wyrazy ze zmienionym znakiem.

Twierdzenie III
Jeśli obie strony równania pomnożymy lub podzielimy przez tę samą liczbę różną od zera, to otrzymamy równanie równoważne danemu.

Rozwiążmy kilka przykładowych równań stosując powyższe twierdzenia:

Rozwiążmy równanie podane w postaci proporcji

Zastosujmy podstawową własność proporcji, która brzmi: Iloczyn wyrazów skrajnych równy jest iloczynowi wyrazów środkowych. Czyli

5 · (3 – 2x) = 6 · (2 – 3x) (tw. I)

15 – 10x = 12 – 18x (tw. II)

– 10x + 18x = 12 – 15 (tw. I)

8x = – 3 |: 8

x =_3/8

4(x – 5) = 4x – 20 (tw. I)
4x – 20 = 4x – 20 (tw. II)
4x – 4x = 20 – 20 (tw. I)
0 = 0 równość prawdziwa

Każda liczba podstawiona w miejsce x spełnia to równanie np.:
niech x = 1; L = 4 · 1 – 4 · 1 = 0; P = 20 – 20 = 0 L = P
niech x = 2; L = 4 · 2 – 4 · 2 = 0; P = 20 – 20 = 0 L = P
niech x = 10; L = 4 · 10 – 4 · 10 = 0; P = 20 – 20 = 0 L = P

Równanie powyższe ma nieskończenie wiele pierwiastków i nazywamy je tożsamościowym lub nieoznaczonym.

Uwaga!
Może się zdarzyć tak, że równanie nie ma pierwiastka np.:

4(x – 5) = 4x – 6 (tw. I)
4x – 20 = 4x – 6 (tw. II)
4x – 4x = 20 – 6 (tw. I)

0 = 14 równość fałszywa (sprzeczność)
Żadna liczba podstawiona zamiast x nie spełnia równania. Nazywa się ono sprzecznym.

Zapamiętaj!
Z powyższych rozważań wynika, że rozwiązać równanie – to znaczy – znaleźć wszystkie liczby, które spełniają to równanie lub wykazać, że nie ma takich liczb.

II. Nierówności

Jeśli dwa wyrażenia, z których przynajmniej jedno jest algebraiczne, połączymy znakiem > lub <, to otrzymamy nierówność.

Nierówność pierwszego rzędu z jedną niewiadomą mamy wtedy, gdy występuje tylko jedna zmienna literowa w pierwszej potędze.
Rozwiązać nierówność znaczy odpowiedzieć na pytanie, które liczby ją spełniają, czyli znaleźć wszystkie jej rozwiązania.

Nierówność może nie mieć żadnego rozwiązania, np.: nie ma liczby spełniającej nierówność , gdyż kwadrat żadnej liczby nie jest ujemny. Jest to nierówność sprzeczna.

Są też nierówności spełnione przez każdą liczbę, np.: x + 1 < x + 2
x – x < 2 – 1
0 < 1 (prawda)
jest prawdziwa dla każdej wartości x. Zbiorem jej rozwiązań jest zbiór wszystkich liczb. Jest to nierówność tożsamościowa.

Zapamiętaj!
Nierówności są równoważne, gdy mają ten sam zbiór rozwiązań.

Prawdziwe są następujące twierdzenia o nierównościach równoważnych, analogicznie do twierdzeń o równoważności równań.

Twierdzenie I
Jeżeli którąś ze stron nierówności przekształcimy tożsamościowo, to otrzymamy nierówność równoważną danej nierówności.

Twierdzenie II
Jeżeli do obu stron nierówności dodamy lub odejmiemy to samo wyrażenie, to otrzymamy nierówność równoważną danej.

Twierdzenie III a
Jeżeli obie strony nierówności pomnożymy lub podzielimy przez tę samą liczbę dodatnią, otrzymamy nierówność równoważną danej nierówności.

Twierdzenie III b
Jeśli obie strony nierówności pomnożymy lub podzielimy przez tę samą liczbę ujemną i prócz tego zmienimy zwrot nierówności na przeciwny, otrzymamy nierówność równoważną danej nierówności.