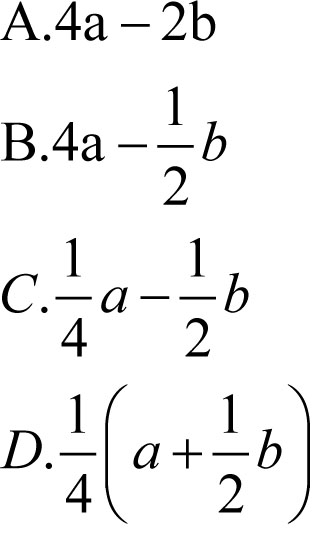Wyrażenia algebraiczne – temat trudny, ale bardzo ważny. Po pierwsze, mogą wystąpić w teście matematyczno-przyrodniczym. Po drugie, bez nich nie rozwiążesz równań, nierówności czy układu równań.
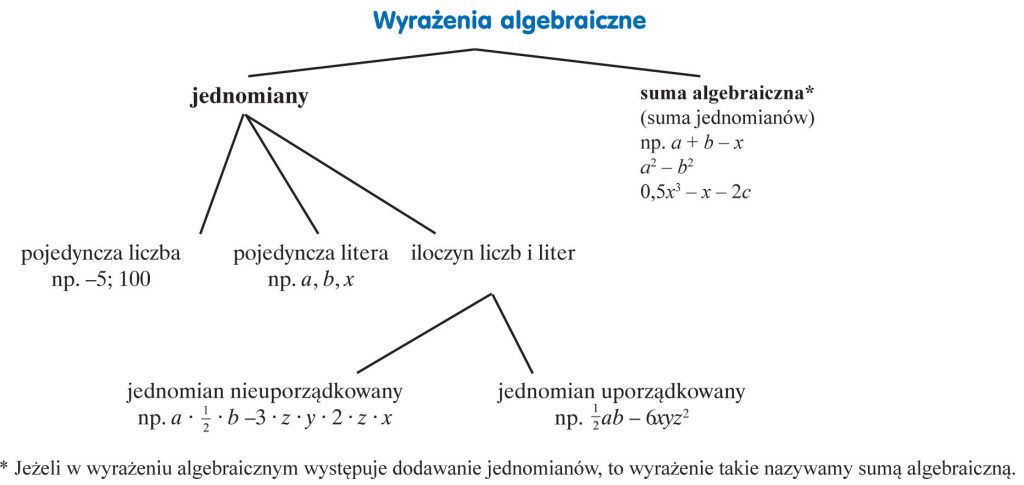
Wyrażenia algebraiczne
Jak je rozpoznać?
Bardzo prosto, bo są to wyrażenia, w których obok liczb, znaków działań, nawiasów występują litery (zmienne), np.
a, 55, – 2xyz, 2x – 7, 3(x² – 3x + 9), a³ + 4a – b – (3a + 6)
Uwaga
W wyrażeniach algebraicznych, w których występuje mnożenie, zwykle nie zapisuje się kropki oznaczającej iloczyn.
Zapisujemy 2x zamiast 2·x. Ten pierwszy zapis jest po prostu krótszy, a oznacza dokładnie to samo.
Powtórz koniecznie!
Odczytywanie i zapisywanie wyrażeń
Po pierwsze, musisz znać kolejność wykonywania działań. Dlaczego? Gdy do wyrażenia algebraicznego zamiast liter wstawisz konkretne liczby i wykonasz wskazane działania, to nazwa ostatniego działania jest nazwą całego wyrażenia.
Zobacz na przykładzie!
Gdyby w wyrażeniu 2 · (x² + 5) w miejsce x podstawić dowolną liczbę, to trzeba by wykonać działania w następującej kolejności:
1) działania w nawiasie: najpierw potęgowanie, potem dodawanie,
2) a potem mnożenie przez 2.
Zatem zgodnie z regułą „idąc od końca” wyrażenie powyższe czytamy jako: iloczyn liczby 2 i sumy kwadratu liczby x i liczby 5.
Poćwicz
1. Różnica czwartej części liczby a i połowy liczby b to:
2. Które z podanych wyrażeń nazwiemy różnicą kwadratu liczby a i sześcianu liczby b:
A. (a² – b)3
B. a² + b³
C. (a – b3)²
D. a² – b³
3. Które z podanych wyrażeń nazwiemy ilorazem kwadratu różnicy liczb m i n przez podwojoną sumę liczb m i n:
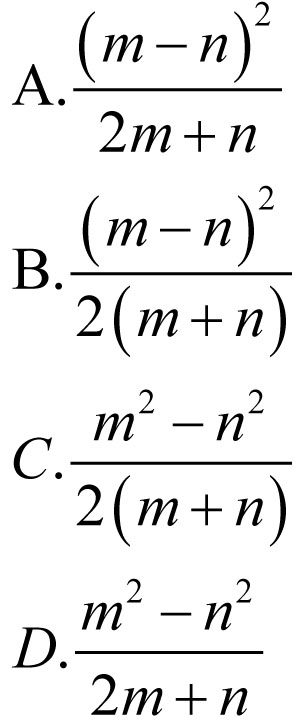
Odpowiedzi: 1.C, 2.D, 3.B.
Obliczanie wartości liczbowej wyrażenia algebraicznego
Zobacz na przykładzie!
Oblicz wartość liczbową wyrażenia
2x² + x – 3 dla x ∈ {–2, –1, 0}.
Dla x = – 2 otrzymujemy:
2 · (–2)² + (–2) – 3 = 2 · 4 – 2 – 3 = 3
Dla x = –1 otrzymujemy:
2 · (–1)² + (–1) – 3 = 2 – 1 – 3 = –2
Dla x = 0 mamy:
2 · 0² + 0 – 3 = –3
Przekształcanie wyrażeń algebraicznych
Wyrazy podobne mają jednakowe czynniki literowe.
1. Redukcja wyrazów podobnych
Zastępujesz wyrazy podobne jednym wyrazem, stosując prawo rozdzielności mnożenia względem dodawania (lub odejmowania).
5a – 7a + 4 = (5 – 7)a + 4 = – 2a + 4
4x² + 9y – 6x² – 4y – 3 = – 2x² + 5y – 3
2. Dodawanie i odejmowanie sum algebraicznych
Dodaj sumy!
(2x² – 3x + 1) + (4x² – 2x – 3) = 2x² – 3x + 1 + 4x² – 2x – 3 = 6x² – 5x – 2
Uwaga! Gdy opuszczasz nawias, przed którym znajduje się znak „+”, to przy każdym wyrazie z nawiasu pozostawiasz niezmieniony znak.
Identyczne sumy teraz odejmij!
(2x² – 3x + 1) – (4x² – 2x – 3) =2x² – 3x + 1 – 4x² + 2x + 3 = – 2x² – x + 4
Uwaga! Gdy opuszczasz nawias, przed którym znajduje się znak „–”, to przy każdym wyrazie z nawiasu musisz zmienić znak na przeciwny.
3. Mnożenie jednomianu przez jednomian
(–3a) · (–4a²b) = (–3) · (–4) · a · a² · b = 12a³b
4. Dzielenie jednomianu przez jednomian
(–16abc) : (–4a) = 4bc
5. Mnożenie jednomianu przez sumę algebraiczną
2a(3a + b – 4c – 1) = 2a · 3a + 2a · b – 2a · 4c – 2a · 1 = 6a² + 2ab – 8ac – 2a
6. Dzielenie sumy algebraicznej przez jednomian
(12a² – 8a) : 2a = 12a² : 2a – 8a : 2a = 6a – 4
7. Mnożenie dwóch sum algebraicznych
(3x + 5)(–x – 1) = 3x · (–x) + 3x · (–1) + 5 · (–x) + 5 · (–1) = –3x² – 3x – 5x – 5 = –3x² – 8x – 5
8. Rozkładanie sum algebraicznych na czynniki
polega na tym, że sumę przekształcamy na iloczyn co najmniej dwóch czynników. W tym celu możemy wykonać kilka czynności:
- wyłączanie wspólnego czynnika poza nawias
np. 8x² – 12xy + 4x = 4x(2x – 3y + 1) - grupowanie wyrazów
np. 5a – 5b + ab – b² = 5(a – b) + b(a – b) = = (a – b)(5 + b) - stosowanie wzorów skróconego mnożenia
np. 25 + 10a + a² = 5² + 2 · 5a + a² = (5 + a)²
Powtórz wzory skróconego mnożenia!
- kwadrat sumy dwóch wyrażeń (a + b)² = a² + 2ab + b²
np. (2x + 5y)² = 4x² + 20xy + 25y²
- kwadrat różnicy dwóch wyrażeń (a – b)² = a² – 2ab + b²
np. (3x – 2y)² = 9x² – 12xy + 4y²
- różnica kwadratów dwóch dowolnych wyrażeń
(a + b) (a – b) = a² – b²
np. (4x + 6)(4x – 6) = 16x² – 36
A teraz test!
Takich zadań spodziewaj się na egzaminie! Rozwiąż je koniecznie – nie daj się nabrać!
1. Zosia ma z lat, Kasia jest od niej o trzy lata starsza. Ile lat miała Kasia cztery lata temu?
A. 4 – z – 3
B. z – 1
C. 4 (z + 3)
D. z – 4
2. Na wycieczkę pojechało 45 osób – kobiety, mężczyźni i dzieci. Mężczyzn było o y mniej niż kobiet. Ile dzieci brało udział w wycieczce, jeżeli liczbę kobiet oznaczymy przez x?
A. 45 – x – x + y
B. 45 – x – x – y
C. 45 – x – y
D. 45 – x + y
3. Wyrażenie a godzin i b minut to:
A. 60(a + b) sekund
B. 60(a – b) sekund
C. 3600a + b sekund
D. 60(60a + b) sekund
4. Wyrażenie x arów i 57 m² to:
A. (100x + 57) [m²]
B. 157x [m²]
C. (1000x + 57) [m²]
D. (10x + 57) [m²]
5. W trójkącie ABC długość boku AB jest równa x cm, bok BC jest o 1 cm krótszy, a bok AC o 2 cm dłuższy od boku BC. Obwód trójkąta wynosi:
A. 3x + 1
B. 3x – 1
C. 3x
D. 3x + 3
6. Pole czworokąta przedstawionego na rysunku wynosi:
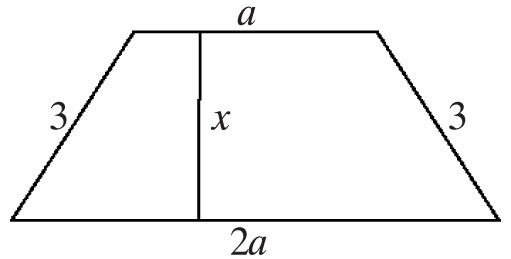
A. 6 + 3a
B. 6 + x + 3a
C. 1,5ax
D. 3ax
7. Dla której z podanych liczb przedstawiony równoległobok jest rombem:
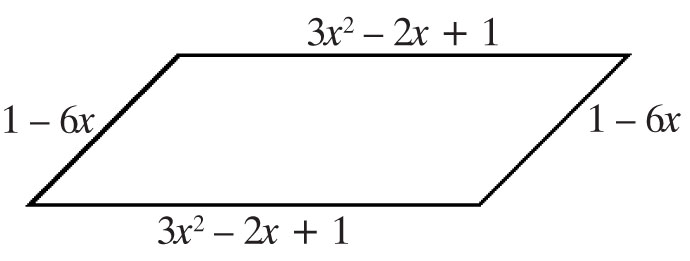
A. x = 0
B. x = – 2
C. x = 1
D. x = – 1
Odpowiedzi:
1. B
2. A
3. D
4. A
5. C
6. C
7. A