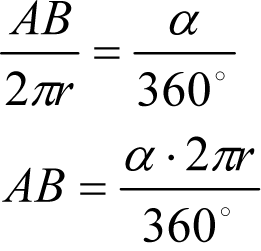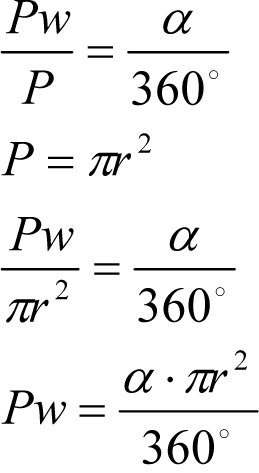Okrąg
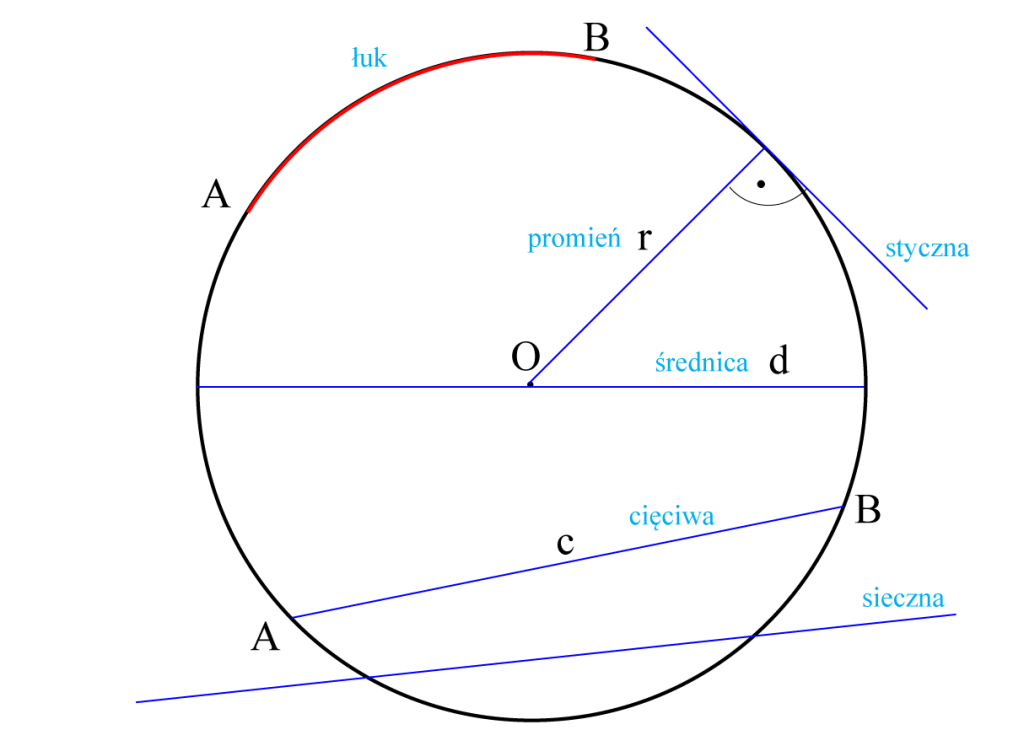
Okręgiem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O wynosi r.
Okręg oznaczamy o (O,r) i czytamy okrąg o środku w punkcie O i promieniu r.
- Promień okręgu jest to odcinek łączący środek okręgu z dowolnym punktem okręgu.
- Cięciwa jest to odcinek łączący dwa dowolne punkty okręgu.
- Średnica jest to cięciwa przechodząca przez środek okręgu.
- Styczna jest to prosta mająca z okręgiem tylko jeden punkt wspólny.
Kąt między styczną do okręgu a promieniem wychodzącym z punktu styczności jest prosty.
- Sieczna jest to prosta przecinająca okrąg w dwóch dowolnych punktach.
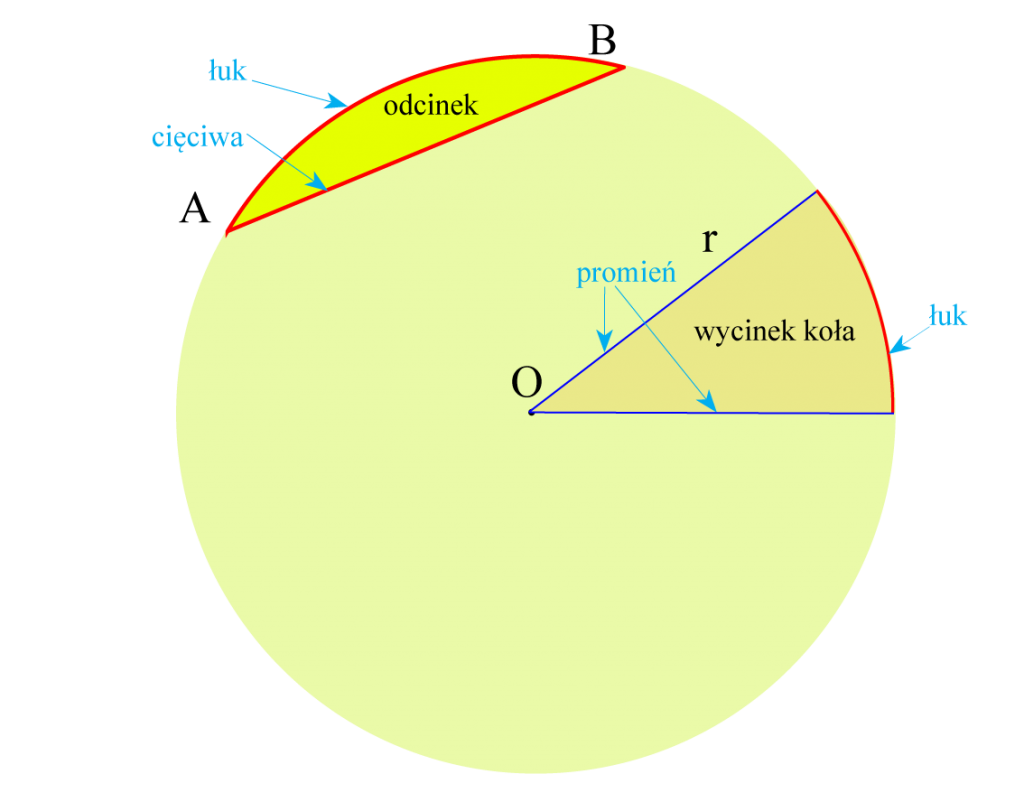
- Łuk jest to dowolny fragment okręgu ograniczony dwoma punktami.
Zapamiętaj!
Środek okręgu nie należy do okręgu, środek koła należy do koła.
WZÓR na długość okręgu
S = 2 πr
Liczba π
- π = 3,14159265358… jest liczbą niewymierną, to znaczy, że jej rozwinięcie dziesiętne jest nieskończone i nieokresowe.
W obliczeniach przyjmujemy zaokrąglenie tej liczby: 3,14.
- Liczba π jest wynikiem ilorazu długości okręgu i długości jego średnicy. Ten stosunek jest wartością stałą, niezależną od wielkości figury.
Koło
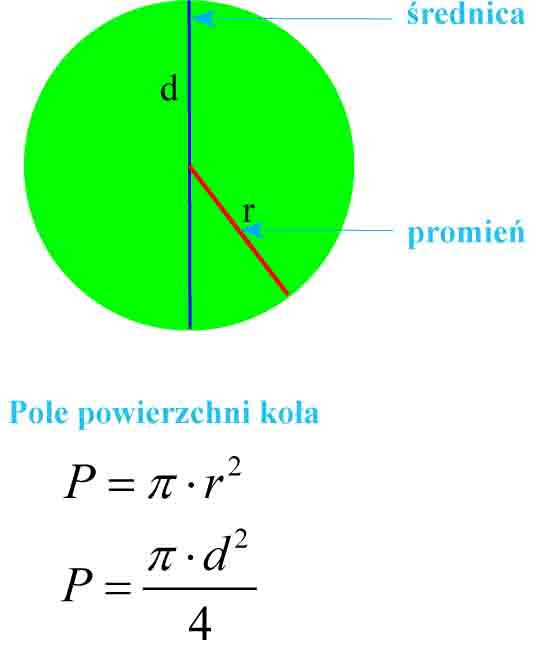
Kołem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O jest mniejsza lub równa r.
Koło oznaczamy k(O,r) i czytamy koło o środku w punkcie O i promieniu r.
- Odcinek koła to część koła zawarta między łukiem a cięciwą koła. Cięciwa dzieli koło na dwie części. Każdą z tych części nazywamy odcinkiem koła.
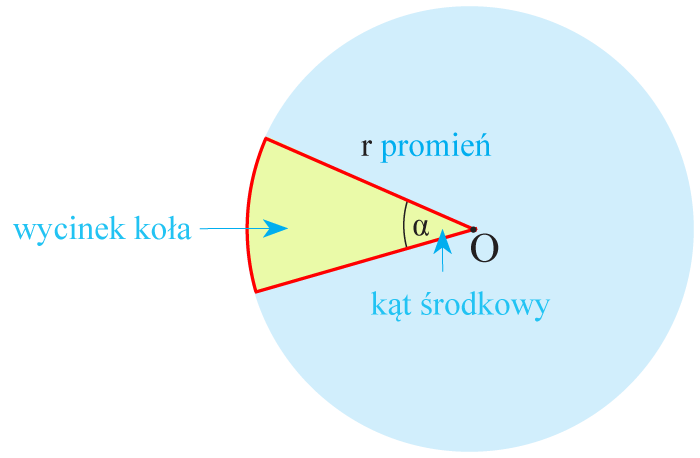
- Wycinek koła to fragment koła zawarty między dwoma promieniami i łukiem koła.
WZÓR na pole koła
WZÓR na obwód koła (długość okręgu)
r – długość promienia koła
P – pole koła
L – obwód koła (długość okręgu)
Zapamiętaj!
- Środek okręgu nie należy do okręgu, środek koła należy do koła.
- Cięciwa dzieli koło na dwie części. Każdą z tych części nazywamy odcinkiem koła.
- Wycinek koła jest częścią powierzchni koła ograniczoną łukiem i dwoma promieniami.
- Pole i obwód koła są ze sobą ściśle związane: większe pole powierzchni to większy obwód, mniejsze pole to mniejszy obwód.
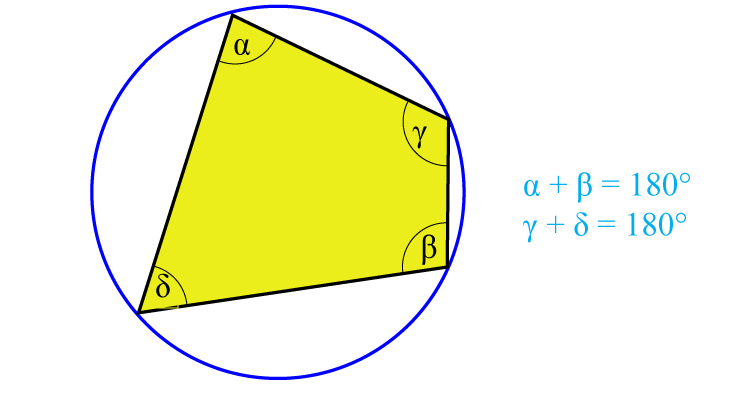
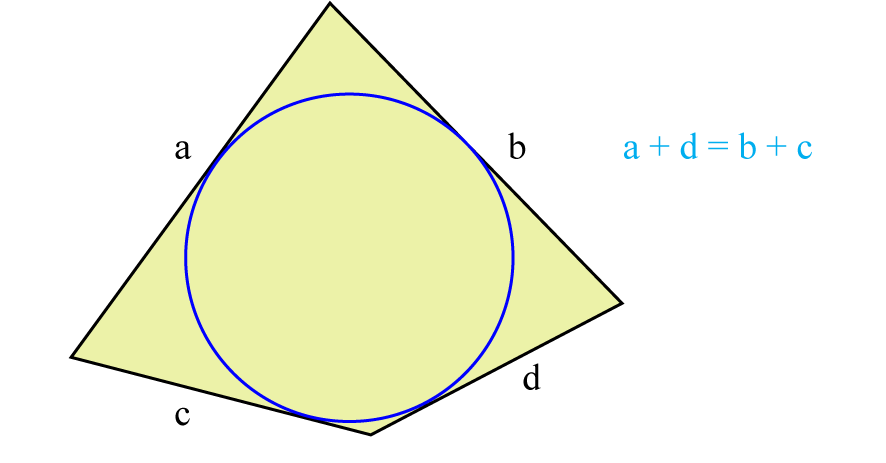
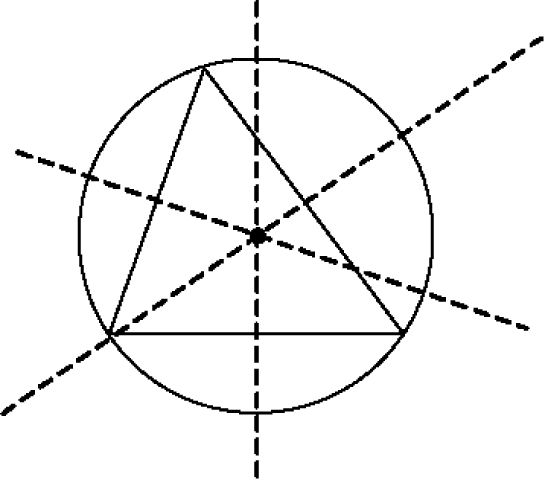
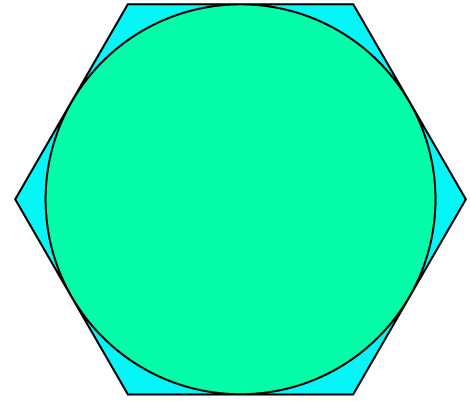
Wielokąt wpisany w okrąg i wielokąt opisany na okręgu
- Czworokąt można wpisać w okrąg, jeżeli sumy przeciwległych kątów są sobie równe i wynoszą 180°.
- Okrąg jest opisany na wielokącie, jeżeli wszystkie wierzchołki tego wielokąta leżą na okręgu.
- Okrąg jest wpisany w wielokąt, jeżeli jest styczny do wszystkich boków tego wielokąta.
Czworokąt można opisać na okręgu, jeżeli sumy przeciwległych boków są sobie równe.
a + c = b + d
Wzajemne położenie prostej i okręgu
- Prosta nie ma punktów wspólnych z okręgiem.
Odległość środka okręgu od prostej jest większa od długości promienia.
- Prosta ma jeden punkt wspólny z okręgiem.
Odległość środka okręgu od prostej jest równa długości promienia.
- Prosta ma dwa punkty wspólne z okręgiem.
Odległość środka okręgu od prostej jest mniejsza od długości promienia.
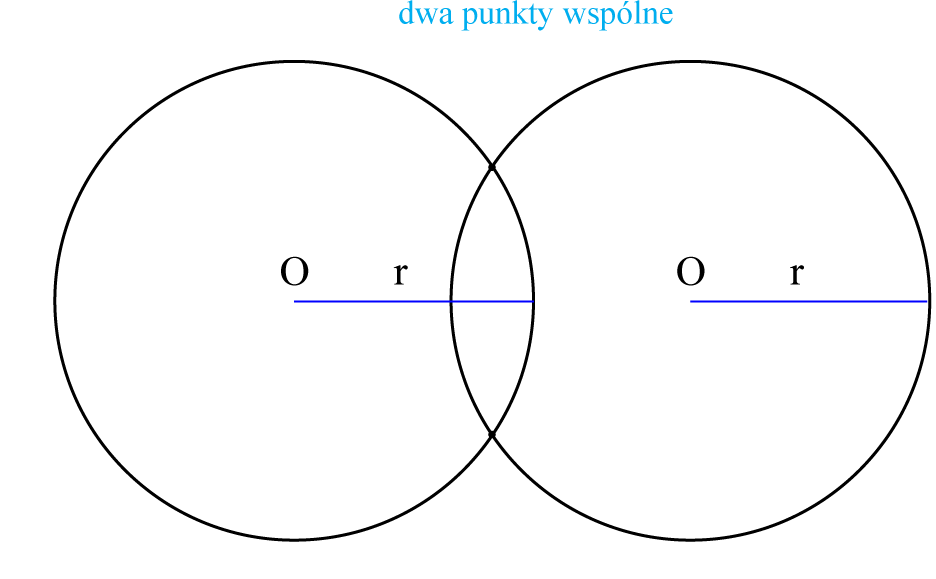
Położenie dwóch okręgów względem siebie
- ROZŁĄCZNE
Brak punktów wspólnych.
- STYCZNE
Jeden punkt wspólny (punkt styczności).
- PRZECINAJĄCE SIĘ
Dwa punkty wspólne.
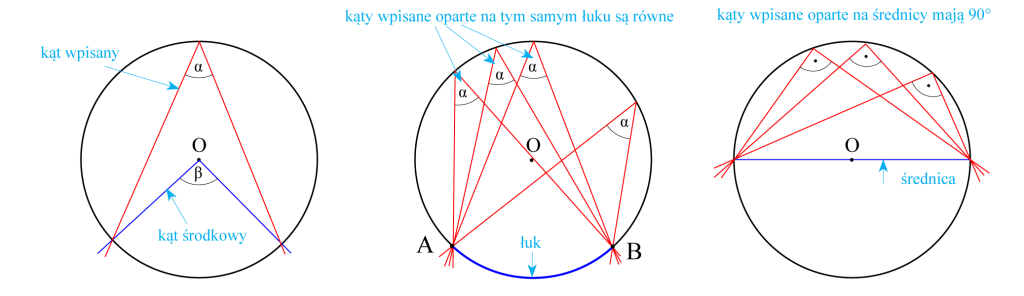
Kąty w kole
Zapamiętaj!
Kąt środkowy to taki, którego wierzchołek leży w środku okręgu.
- Kąt środkowy ma miarę dwa razy większą od kąta wpisanego opartego na tym samym łuku.
- Im większy kąt środkowy, tym dłuższy odpowiadający mu łuk AB.
- Kąt środkowy oparty na połowie okręgu to kąt półpełny (180°).
- Im większy kąt środkowy , tym dłuższy odpowiadający mu łuk AB.
Kąt wpisany to kąt wypukły, którego wierzchołkiem leży na okręgu a jego ramiona przecinają się z okręgiem i zawierają cięciwy tego okręgu.
- Kąty wpisane oparte na tym samym łuku mają równe miary.
- Kąt wpisany oparty na połowie okręgu jest prosty (ma miarę 90°).
- Wszystkie kąty wpisane oparte na średnicy mają 90°.
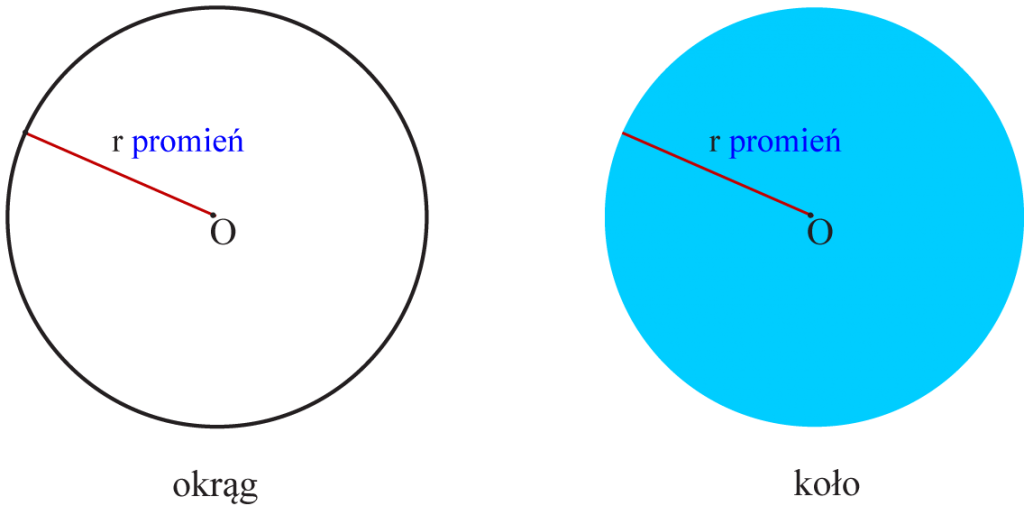
Czym się różnią okrąg i koło?
Okręgiem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O wynosi r.
Kołem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległość od punktu O jest mniejsza lub równa r.
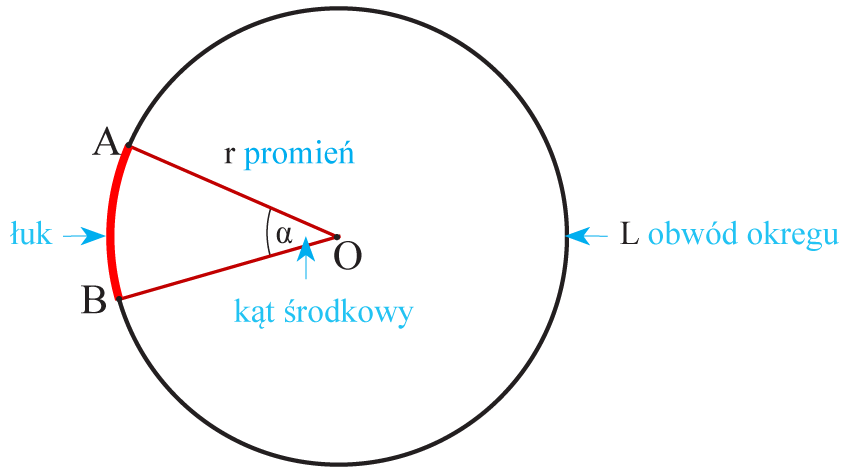
Długość łuku
Łuk jest określony przez promień okręgu r i kąt środkowy α. Długość zaznaczonego łuku AB i obwód okręgu L pozostają w takim samym stosunku względem siebie jak kąt środkowy α i kąt pełny 360°.
L = 2πr
Długość łuku Ł wycinka koła o promieniu r wyciętego przez kąt środkowy o mierze α jest równa ![]() I to jest wzór na obliczanie długości łuku.
I to jest wzór na obliczanie długości łuku.
Zauważ! Im większy kąt środkowy α, tym dłuższy odpowiadający mu łuk AB.
Pole wycinka koła
Zaznaczonemu na rysunku wycinkowi koła odpowiada kąt środkowy α. Pole tego wycinka koła Pw i pole koła P pozostają w takim samym stosunku względem siebie jak kąt środkowyα i kąt pełny 360°.
Pw – pole wycinka koła
P – pole koła
r – promień koła
Pole wycinka koła o promieniu r wyciętego przez kąt środkowy o mierze α jest równe ![]() .
.
To koniecznie zapamiętaj!
Symetralna odcinka to prosta doń prostopadła i przechodząca przez jego środek. Symetralne boków trójkąta przecinają się w jednym punkcie; punkt ten jest środkiem okręgu opisanego na tym trójkącie.
Dwusieczna kąta to półprosta wychodząca z jego wierzchołka i dzieląca go na dwa kąty równej miary. Dwusieczne kątów trójkąta przecinają się w jednym punkcie; punkt ten jest środkiem okręgu wpisanego w ten trójkąt.
Skojarz rysunek!
To jest ważne!
W okręgu i kole można zaznaczyć:
- Promień – odcinek, którego jednym końcem jest środek okręgu O, a drugi koniec leży na okręgu.
- Cięciwa – odcinek, którego oba końce leżą na okręgu.
- Średnica – cięciwa przechodząca przez środek okręgu O.
- Łuk – część okręgu zawarta między dwoma różnymi punktami okręgu wraz z tymi punktami.
Zadania
1. Ile stopni ma kąt środkowy oparty na 5/6 okręgu?
Odpowiedź:
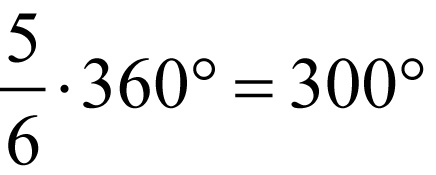
2. Ile stopni ma kąt wpisany oparty na 5/6 okręgu?
Odpowiedź:
![]()
3. Ile stopni ma kąt środkowy oparty na półokręgu?
Odpowiedź:
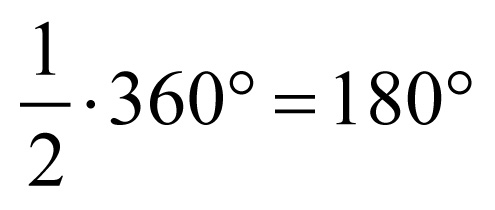
4. Ile stopni ma kąt wpisany oparty na półokręgu?
Odpowiedź:
![]()
5. Ile stopni ma kąt środkowy oparty na 1/3 okręgu?
Odpowiedź:
![]()
6. Oblicz miary kątów wpisanych α, β, jeżeli łuk AB, na którym oparte są te katy, stanowi 1/3 długości okręgu.
Odpowiedź:
![]()
Poćwicz
Pamiętaj o właściwym wykonaniu rysunków, czytaj wnikliwie treści pytań, uważaj na „haczyki” w nich zawarte!
1. Kąt środkowy ma 240°. Łuk, na którym opiera się ten kąt, stanowi:
A. 1/3 okręgu.
B. 2/3 okręgu.
C. 2/5 okręgu.
D. 5/6 okręgu.
2. Miara kąta wpisanego opartego na 7/9 okręgu wynosi:
A. 140°
B. 210°
C. 280°
D. 150°
3. Zegar w kształcie sześciokąta foremnego o obwodzie 24 cm ma w środku okrągłą tarczę. Długość średnicy tej tarczy wynosi:![]()
4. Jeżeli miara kąta AOC wynosi 40°, a miara kąta COB jest równa 70°, to miary kątów trójkąta ABC wynoszą:

A. 35°, 20°, 125°
B. 40°, 70°, 70°
C. 35°, 20°, 135°
D. 80°, 140°, 200°
5. Prosta k jest styczna do okręgu. Kąt ma miarę:
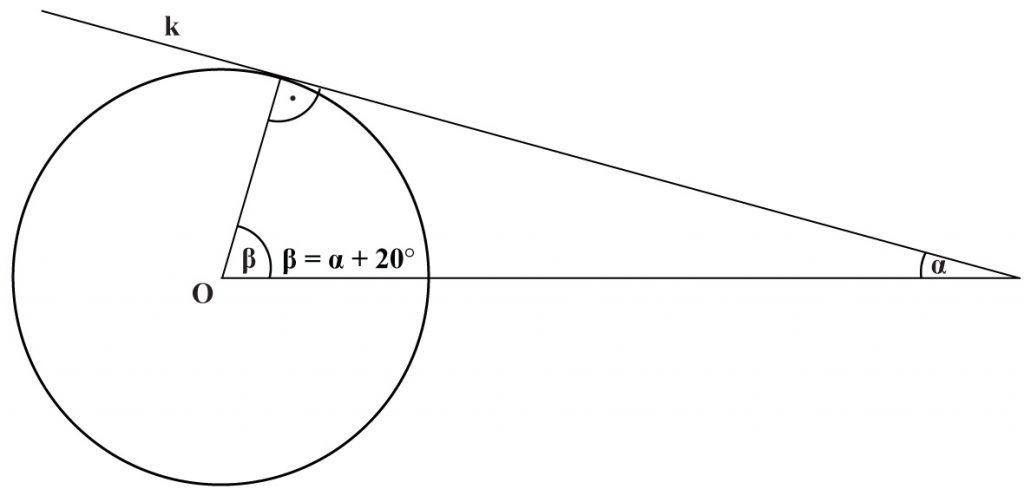
A. 25°
B. 35°
C. 45°
D. 80°
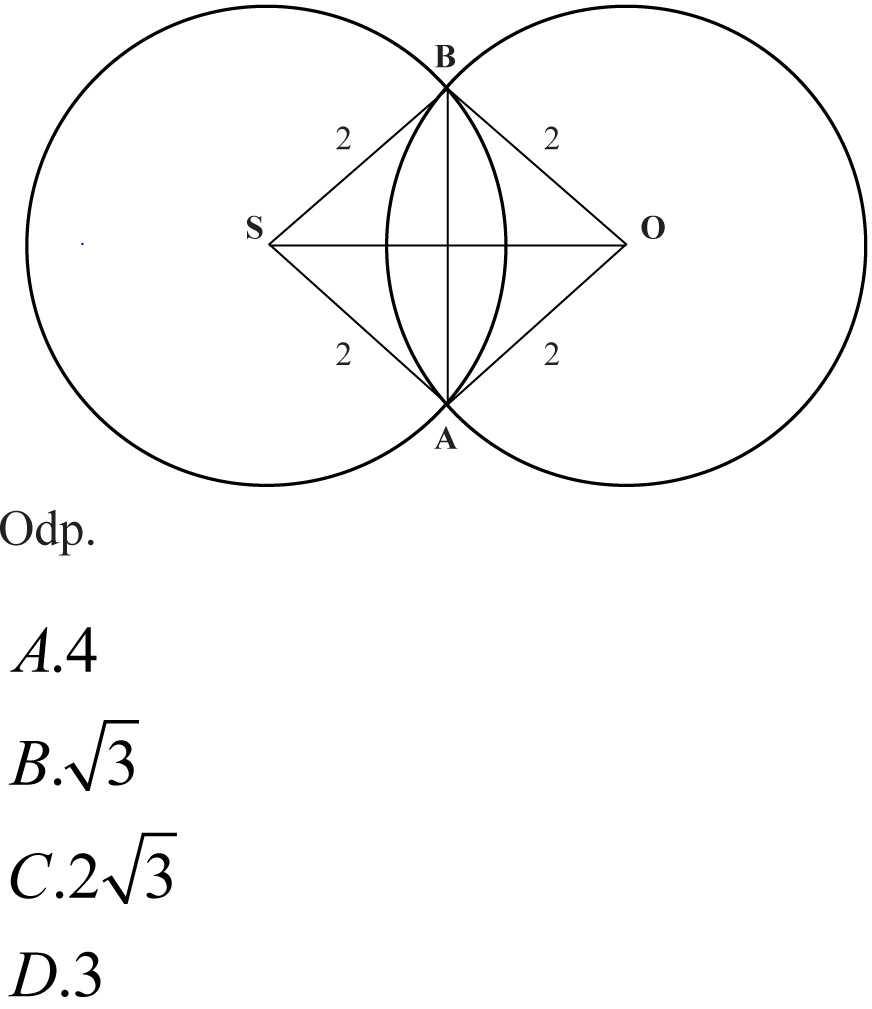
6. Jaka jest długość odcinka OS, jeżeli miary kątów ASB i AOB wynoszą 60°?
Odpowiedzi: 1. B, 2. A, 3. C, 4. A, 5. B, 6. C.