Czym są zbiory?

Najprościej: zbiór to zestaw pewnych elementów. Jakie to mogą być elementy? Najróżniejsze! A najważniejsze jest to, że musisz znać regułę, która określi, jakie elementy będą należały do zbioru. Na przykład jeśli określisz, że do zbioru będą należały tylko domy z czerwonymi dachami, to dom z zielonym dachem znajdzie się poza zbiorem. Sam należysz do zbioru. Jakiego? Na przykład do zbioru osób między drugim a dwudziestym drugim rokiem życia czy do zbioru osób objętych w Polsce obowiązkiem szkolnym. Jest też nieskończenie wiele różnych zbiorów, do których nie będziesz należał. Na przykład zbiór uczniów nieumiejących czytać albo zbiór ludzi urodzonych przed rokiem 1435. Wszystko zależy od tego, jak dany zbiór określimy, czyli zdefiniujemy.

Zapamiętaj!
Zbiór to zestaw elementów należących do określonej kategorii.

 

Jakie mogą być zbiory?

Skojarz trzy opcje:

  • Opcja I
    Zbiory mogą mieć określoną liczbę elementów, np. takim zbiorem będzie zbiór dni tygodnia. Dlaczego? Bo ten zbiór ma określoną liczbę elementów, jest ich 7: {poniedziałek, wtorek, środa, czwartek, piątek, sobota, niedziela}
    Zbiór mający określoną liczbę elementów to zbiór skończony.
  • Opcja II
    Zbiory mogą mieć nieskończenie wiele elementów, np. taki zbiór tworzą gwiazdy na niebie. Przecież nie wiemy, ile ich jest.
    Zbiór mający nieskończenie wiele elementów to zbiór nieskończony.
  • Opcja III
    Istnieje też zbiór, który nie ma żadnych elementów. Jak się nazywa? To zbiór pusty.

Czym są zbiory liczbowe?
To zbiory, w których elementami są liczby.

Zanim powtórzysz działania na zbiorach liczbowych, przypomnij sobie całą rodzinkę liczb!

  • Liczby całkowite to liczby 1, –1, 2, – 2, 3, – 3, 4, – 4, 5, – 5, 6, – 6 itd. Wyróżniamy wśród nich
    • liczby całkowite dodatnie, np. 1, 2, 3, 4, itd.,
    • liczby całkowite ujemne, np. – 1, – 2, – 3 itd.
  • Liczby naturalne to wszystkie liczby całkowite nieujemne, to znaczy: 1, 2, 3, 4, 5, 6, 7 i tak dalej…
    Uwaga! Do liczb naturalnych należy także zero. Jest ono najmniejszą liczbą w tym zbiorze.
    A która liczba jest największa? Nie możemy takiej określić, ponieważ liczb jest nieskończenie wiele.
    Czy wiesz, jak nazywają się wielkie liczby używane w Polsce? Będą to kolejno: milion, bilion, trylion, kwadrylion, kwintylion, sekstylion, septylion, oktylion, nonilion, decylion itd. aż do nieskończoności…
  • Liczby wymierne to wszystkie liczby dające się zapisać za pomocą ułamka zwykłego, w którym licznik i mianownik są liczbami całkowitymi a mianownik jest liczbą różną od zera (bo nie wolno dzielić przez zero). Do zbioru liczb wymiernych należą więc wszystkie liczby całkowite oraz wszystkie ułamki zwykłe.

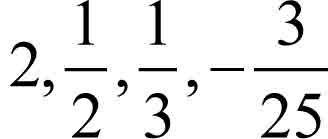
Każdą liczbę naturalną czy całkowitą także możemy zapisać w postaci ułamka, np.

  • Liczby niewymierne to te wszystkie liczby rzeczywiste, które nie są liczbami wymiernymi; mają swoje miejsce na osi liczbowej, ale nie da się ich przedstawić w postaci ułamka zwykłego, w którym licznik i mianownik są liczbami całkowitymi, np..
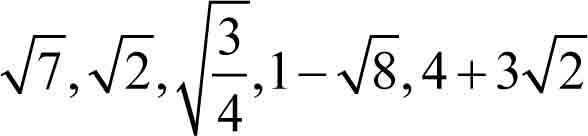
  • Liczby rzeczywiste to wszystkie liczby wymierne i niewymierne.

Zapamiętaj symbole!

  • R – zbiór wszystkich liczb rzeczywistych
  • IW – zbiór liczb niewymiernych
  • W – zbiór liczb wymiernych
  • C – zbiór liczb całkowitych
  • N – zbiór liczb naturalnych

Czym są liczby pierwsze?
To wszystkie liczby naturalne większe od 1, których jedynymi dzielnikami są liczby: 1 i dana liczba.

Czym jest dzielnik liczby?
To liczba, która dzieli bez reszty daną liczbę.

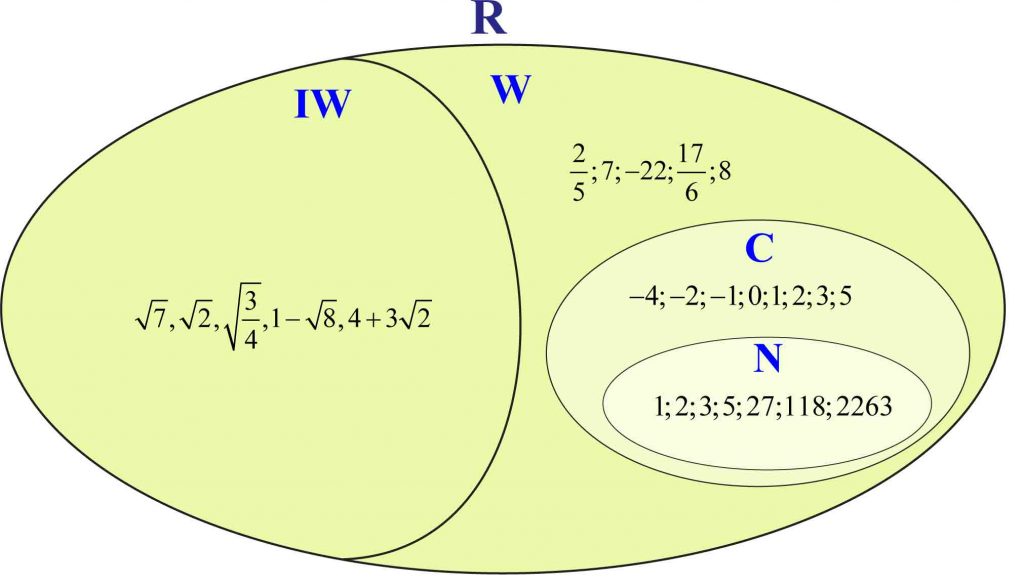
Poniższy rysunek pozwoli łatwo zapamiętać, jakie liczby należą do poszczególnych zbiorów.

Co wynika z tego rysunku?

Każda liczba naturalna jest więc liczbą całkowitą, każda liczba całkowita jest liczbą wymierną, każda zaś liczba wymierna jest liczbą rzeczywistą. Zbiór liczb naturalnych zawiera się w zbiorze liczb całkowitych, zbiór liczb całkowitych w zbiorze liczb wymiernych, a zbiór liczb wymiernych w zbiorze liczb rzeczywistych.

Jak określić, które elementy należą do danego zbioru? Spójrz na przykład!

Niech zbiór A będzie zbiorem liczb całkowitych większych od –8 i będących wielokrotnością liczby 7. Na tej podstawie możemy jasno określić, które z przykładowych elementów będą do niego należały. Zaczynamy:

  • Pies – nie, bo nie jest liczbą!
  • –123,8 – nie, bo jest mniejsze od – 8 i na dodatek nie jest całkowite!
  • 5 – też nie, bo nie jest wielokrotnością liczby 7!
  • 28 – tak, bo spełnia wszystkie trzy warunki!

 

Działania na zbiorach

Zbiory, podobnie jak liczby, możesz dodawać, odejmować lub mnożyć.

Suma zbiorów A i B to zbiór tych elementów, które należą do zbioru A lub B. Zapamiętaj symbol: A ∪ B to suma zbiorów A i B.
Skojarz rysunek!

. A ∪ B

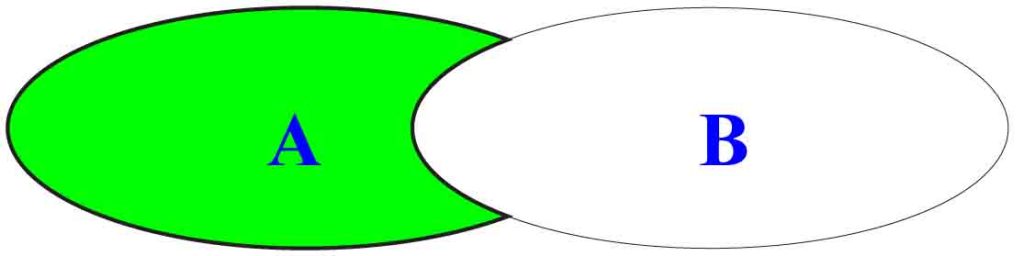
Różnica zbiorów A i B to zbiór elementów, które należą do zbioru A i nie należą do zbioru B. Zapamiętaj symbol: A\B to różnica zbiorów A i B.
Skojarz rysunek!

. A\B

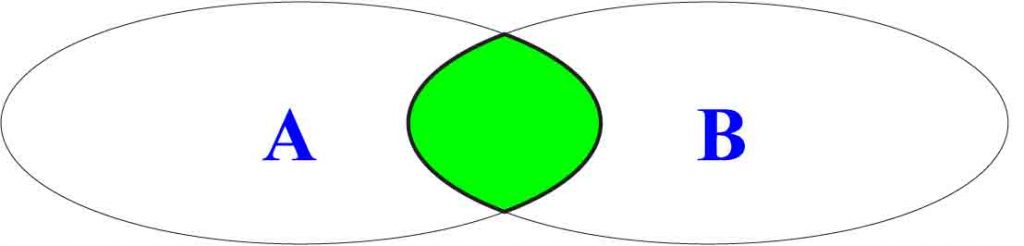
Iloczyn zbiorów A i B to zbiór elementów, które należą jednocześnie do zbioru A i do zbioru B. Zapamiętaj symbol: A ∩ B to iloczyn zbiorów A i B, czyli ich część wspólna.
Skojarz rysunek!

. A ∩ B

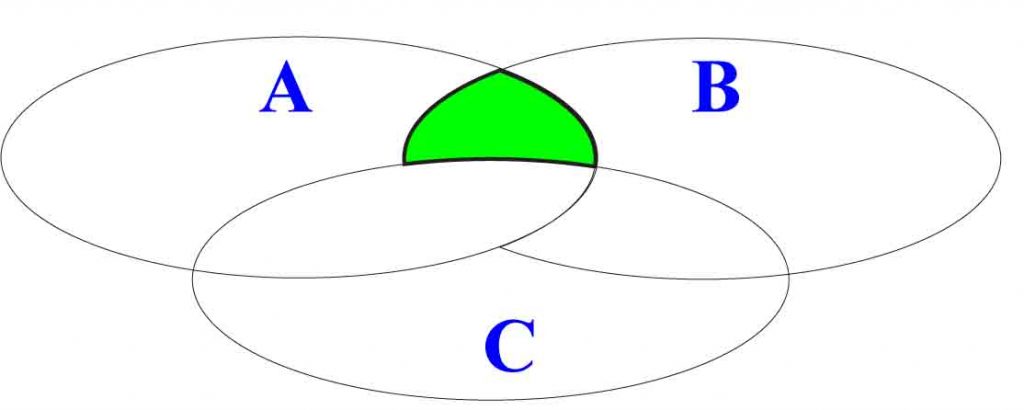
Możesz też wykonywać działania złożone, na przykład: (A ∩ B)\C.
Co to znaczy? Od części wspólnej zbiorów A i B trzeba odjąć zbiór C.
Tak będzie wyglądał rysunek!

. (A ∩ B)\C

Zapamiętaj symbole!

  • suma zbiorów: A ∪ B
  • różnica zbiorów: A\B
  • Iloczyn zbiorów (część wspólna): A ∩ B
  • A ⊂ B zbiór A zawiera się w zbiorze B, czyli A jest podzbiorem zbioru B.

 

Czym jest przedział liczbowy?

Przedział liczbowy to nic innego jak zbiór liczb. A teraz ważne definicje:

Przedział liczbowy otwarty (a; b) to zbiór wszystkich liczb rzeczywistych mniejszych od b i jednocześnie większych od a. Czyli liczby a i b do niego nie należą. Jakiś przykład? Przedział to zbiór wszystkich liczb, które są mniejsze od 71/2, ale większe od 3. Oto 10 przykładowych liczb należących do tego przedziału: .

Przedział liczbowy domknięty 〈a; b〉 to zbiór wszystkich liczb rzeczywistych nie większych od b i jednocześnie nie mniejszych od a. Czyli liczby a i b należą do tego przedziału. Na przykład: jeśli do przedziału otwartego dodamy zbiór dwuelementowy , to otrzymamy przedział domknięty :

Zadanie
Oblicz różnicę zbiorów A \ B, gdzie, . Jak to zrobić?
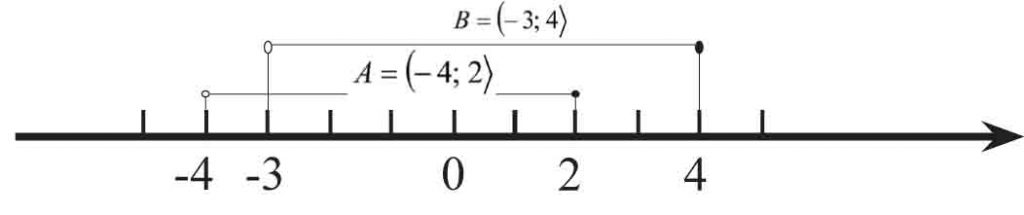
Zacznij od rysunku. Zwróć szczególną uwagę na krańce przedziałów.

Teraz zasłoń ręką zbiór, który odejmujesz, czyli przedział (-3;4〉. Co zostało?
Przedział od – 4 do – 3.
Zapisz to matematycznie (-4;-3).
A co z liczbą – 3? Przecież zbiór B jest lewostronnie otwarty, czyli minus trzy do niego nie należy.
Czyli prawidłowy zapis to: (– 4, – 3〉.

Zobacz:

Zbiory liczbowe