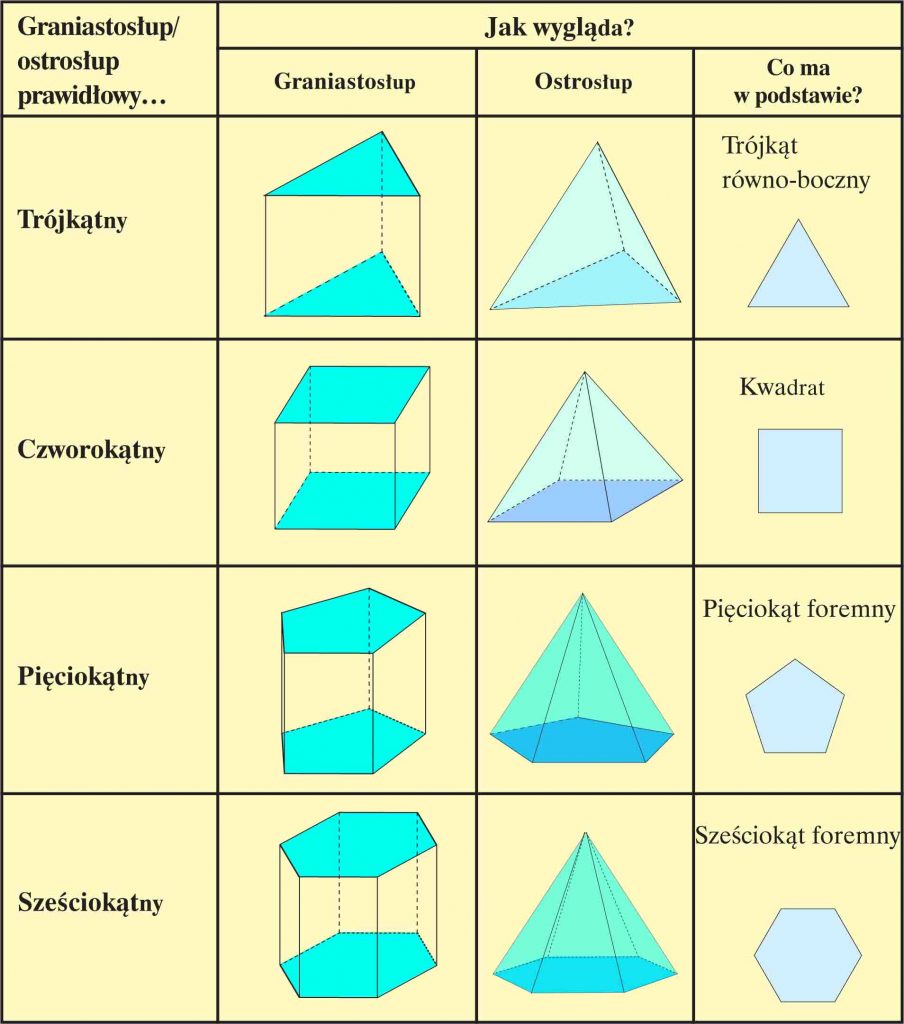
Nie trzeba mieć wybitnej wyobraźni przestrzennej, aby prawidłowo rozwiązywać zadania dotyczące brył. Trzeba tylko umieć każdą z tych brył narysować i znać wzory na objętość i pole powierzchni całkowitej.
Zapamiętaj!
Stereometria to geometria przestrzenna.
To koniecznie powtórz przed egzaminem!
- Rozpoznawanie brył (odróżnianie graniastosłupa od ostrosłupa, graniastosłupa prawidłowego od prostopadłościanu).
- Obliczanie pola powierzchni całkowitej i objętości brył.
Musisz umieć odróżnić…
- …wysokość bryły od wysokości ściany bocznej.
- …krawędź podstawy od krawędzi bocznej.
Spójrz na przykład!
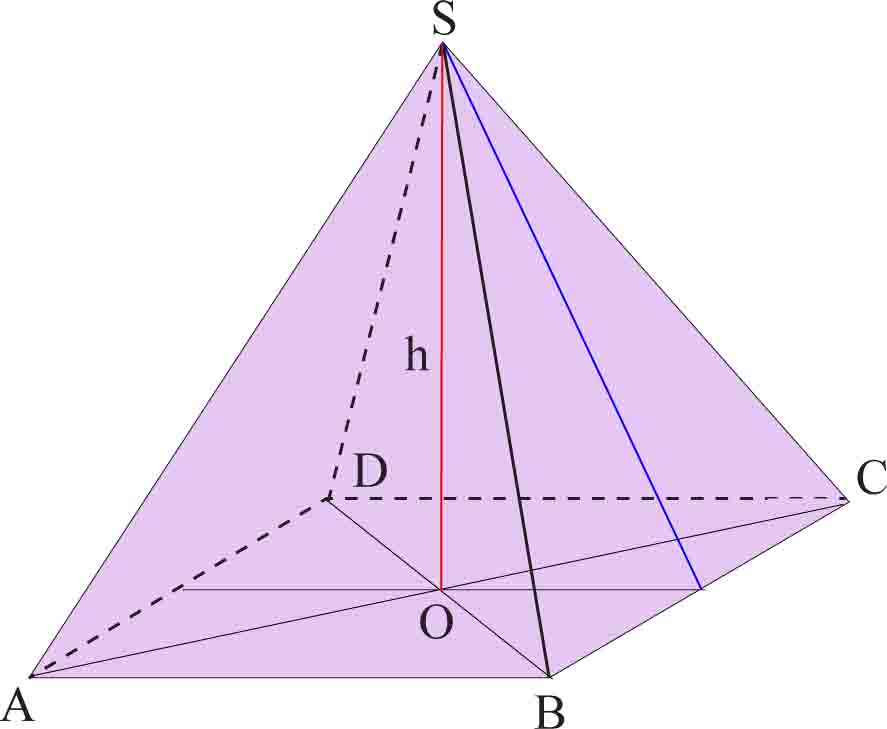
Na rysunku poniżej przedstawiony jest ostrosłup prawidłowy czworokątny.
Wysokość ostrosłupa h to odcinek łączący wierzchołek bryły (S) z rzutem wierzchołka na podstawę (O).
Wysokość ściany bocznej to po prostu wysokość trójkąta równoramiennego (np. BCS).
Spójrz na rysunek i zobacz, że:
- Odcinek OS to wysokość ostrosłupa.
- Odcinek LS to wysokość ściany bocznej ostrosłupa.
- Odcinki AB, BC, CD, DA to krawędzie podstawy ostrosłupa.
- Odcinki AS, BS, CS, DS to krawędzie boczne ostrosłupa.
Zapamiętaj!
Bryły obrotowe
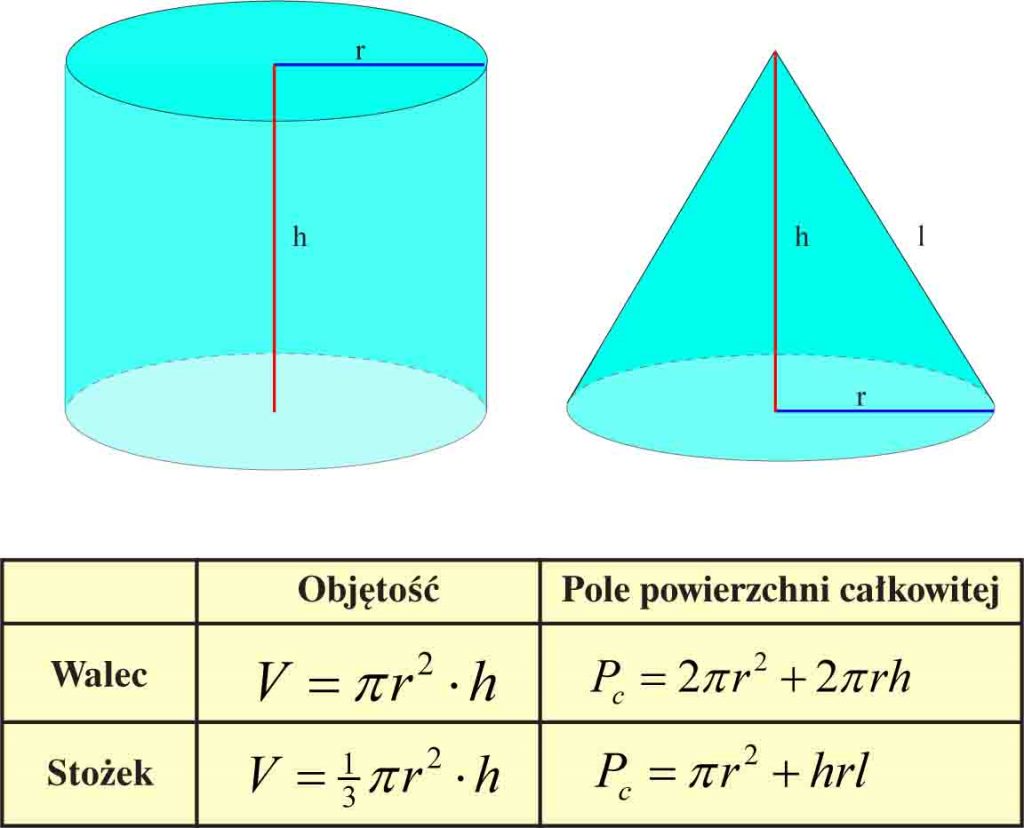
Osobną grupę brył stanowią tzw. bryły obrotowe (powstałe przez obrót figur płaskich, np. wokół ich osi symetrii). Bryły obrotowe, które musisz znać, to: walec, stożek i kula.
To jest ważne!
Nawet jeśli podstawy i wysokości stożka i walca są identyczne, to bryły te mają różne pola powierzchni całkowitych i objętości!
Takie zadanie może pojawić się na egzaminie!
Zadanie
Jeżeli długość krawędzi sześcianu zwiększymy dwa razy, to pole powierzchni całkowitej i objętość tego sześcianu wzrosną odpowiednio:
A. dwa razy, cztery razy
B. cztery razy, osiem razy
C. zarówno objętość, jak i pole wzrosną dwa razy
D. tego nie da się obliczyć bez podanej długości krawędzi sześcianu
Jak to rozwiązać?
Jeżeli wszystkie krawędzie bryły lub figury płaskiej zmienimy proporcjonalnie, to otrzymamy bryłę (figurę) podobną. Pole powierzchni jest iloczynem dwóch długości, a objętość – iloczynem trzech długości. Zatem pole powierzchni rośnie proporcjonalnie do kwadratu (drugiej potęgi), a objętość – do sześcianu (trzeciej potęgi) skali podobieństwa.
Jeśli długość krawędzi sześcianu zwiększymy dwukrotnie, to pole powierzchni zwiększy się 2² (czyli 4) razy, a objętość – 2³ (czyli 8) razy. Zatem prawidłowa odpowiedź to B.
Co to jest prostopadłościan?
Prostopadłościan to taki graniastosłup, którego wszystkie ściany są prostokątami. W naszym otoczeniu jest dużo graniastosłupów: pudełko zapałek, pudełko od kasety magnetofonowej, książka.
- Prostopadłościan jest graniastosłupem prostym (bo jego ściany boczne są prostokątami).
- W ogólnym przypadku prostopadłościan NIE JEST graniastosłupem prawidłowym (bo jego podstawy nie muszą być kwadratami).
Zadanie 1.
Długości krawędzi prostopadłościanu pozostają w stosunku 2:3:5. Najkrótsza krawędź ma długość 4. Oblicz pole powierzchni całkowitej i objętość prostopadłościanu.
Jak to rozwiązać?
Najpierw wykonaj rysunek:
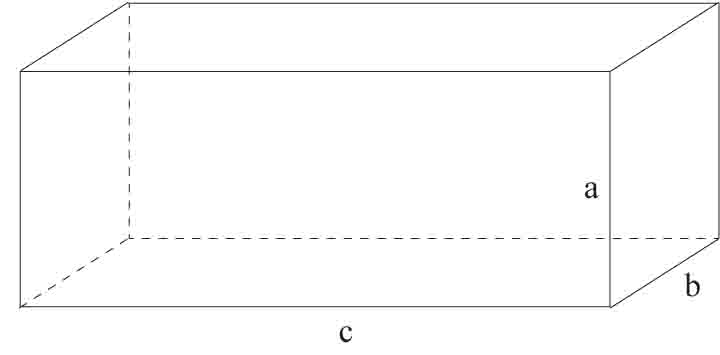
Najkrótszą krawędź prostopadłościanu oznaczmy przez a, najdłuższą przez c. Wtedy:
![]()
Ponieważ a = 4, więc: b = 6; c = 10
Obliczamy pole powierzchni całkowitej:
Objętość: V = a . b . c = 4 . 6 . 10 = 240.
Zapamiętaj, że pole powierzchni całkowitej podajemy w jednostkach kwadratowych, objętość natomiast w jednostkach sześciennych.