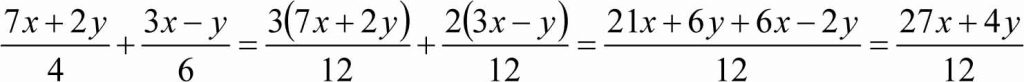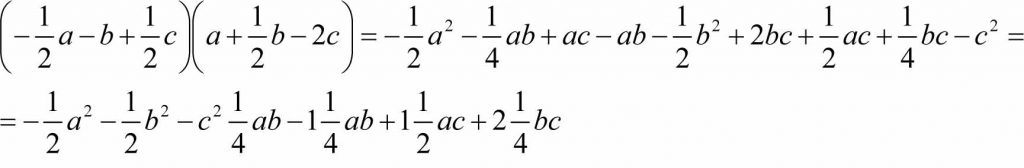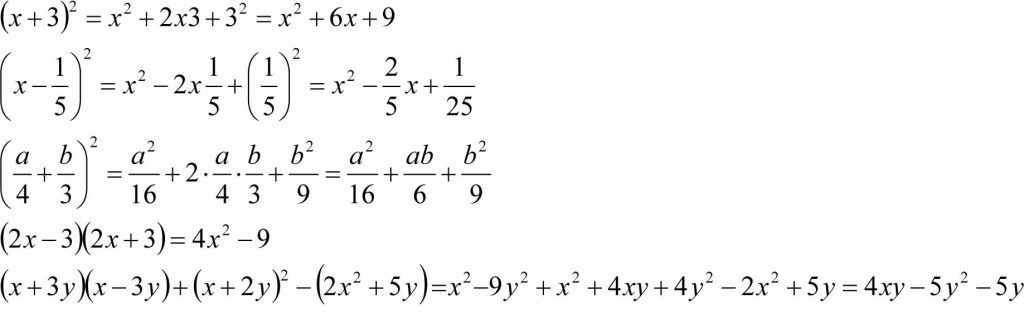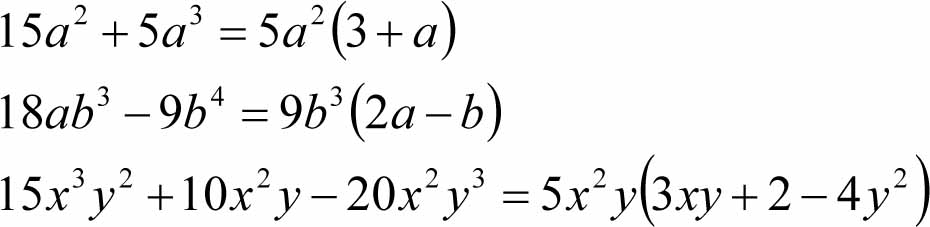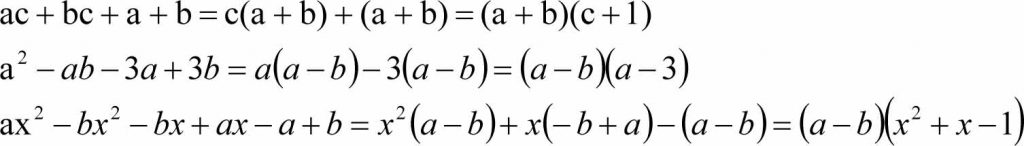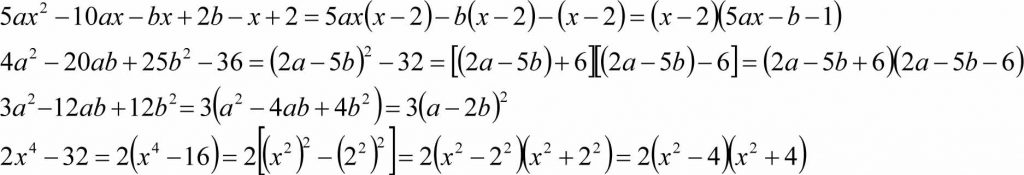WYRAŻENIEM (w sensie matematycznym) nazywamy pojedynczą liczbę lub zmienną literową, albo kilka liczb czy zmiennych literowych połączonych znakami działań. Np.:
Wyrażenia dzielimy na:
1. ARYTMETYCZNE, jeśli występują tylko elementy zbiorów liczbowych.
5 +2; ![]() ; 8 – (-4); – to wyrażenia arytmetyczne (nie zawierają liter (zmiennych);
; 8 – (-4); – to wyrażenia arytmetyczne (nie zawierają liter (zmiennych);
2. ALGEBRAICZNE (lub literowe) – jeśli występuje chociażby jedna zmienna literowa.
2x; 5x – 9; 4(a + p) – to wyrażenia algebraiczne (tworzymy przez połączenie symboli literowych oraz liczb znakami działań i nawiasów).
Każde wyrażenie, czy to arytmetyczne, czy też algebraiczne, posiada swoją nazwę, którą bierze od ostatniego wykonywanego działania, np.:
2x – y – różnica iloczynu 2 przez x i zmiennej y;
a² + b² – suma kwadratów zmiennych a i b;
2(x+y)³- iloczyn liczby 2 i sześcianu sumy zmiennych x i y;
![]() – iloczyn, którego licznik jest różnicą iloczynów 5 przez a i 2 przez b a mianownik liczbą 6
– iloczyn, którego licznik jest różnicą iloczynów 5 przez a i 2 przez b a mianownik liczbą 6
Wyrażenie algebraiczne nie posiada określonej wartości liczbowej, dopóki nie wstawimy w miejsce zmiennych (liter) konkretnych liczb. Wyrażenie algebraiczne zamienia się wtedy w wyrażenie arytmetyczne o ustalonej wartości liczbowej. Np.
![]()
dla a = 1 i b = -2, posiada wartość:
To samo wyrażenie dla a = -2 i b = 3, posiada wartość:
Prostymi wyrażeniami algebraicznym są jednomiany – wyrażenia, która są pojedynczymi liczbami, literami lub iloczynami liczb i liter, np.
4y, 3y, z, -3, 5ab itd.
Zapamiętaj!
JEDNOMIANEM nazywamy iloczyn czynników cyfrowych lub literowych, albo pojedynczy znak liczby, czy zmiennej literowej.
Bardzo ważną czynnością jest uporządkowanie jednomianu.
Uporządkować jednomian, to znaczy:
- Wymnożyć wszystkie czynniki cyfrowe,
- Ułożyć zmienne literowe w kolejności alfabetycznej,
- Zastąpić iloczyn jednakowych zmiennych literowych, ich potęgą,
Uporządkujmy jednomian:
- 1. Mnożymy czynniki cyfrowe ustalając współczynnik całego jednomianu.
- 2. zmienne układamy w kolejności alfabetycznej
- 3. jednakowe czynniki zastępujemy potęgą
Zatem uporządkowany jednomian ma postać ładniejszą niż początkowy, a mianowicie
Jednomiany można dodawać, odejmować, mnożyć i dzielić.
1. Mnożąc dwa lub więcej jednomianów, otrzymamy jednomian, np.:
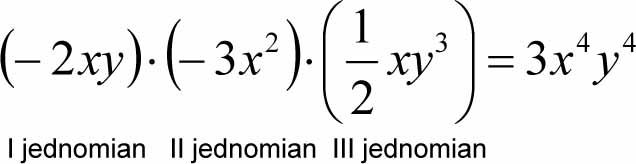
Wynik mnożenia jest jednomianem
2. Dzieląc dwa jednomiany otrzymamy UŁAMEK ALGEBRAICZNY, np.:
Ułamek ma sens liczbowy tylko wtedy, gdy jego mianownik nie jest równy zero, więc w naszym przykładzie nie wolno podstawiać zamiast d zera.
UŁAMEK ALGEBRAICZNY, to szersze pojęcie niż iloraz dwóch jednomianów. W jego liczniku i mianowniku mogą występować nie tylko jednomiany. Mogą to być wyrażenia algebraiczne i wtedy ułamek przybiera bardziej złożoną postać, np.:
Ułamki algebraiczne można
- lub rozszerzać: mnożąc jego licznik i mianownik przez taki sam jednomian (w tym przypadku 3p).
Ułamki algebraiczne można także:
- dodawać
- odejmować
- mnożyć
- dzielić
stosując te same prawidła jak w działaniach na ułamkach arytmetycznych, np.:
Warto zapamiętać, że:
gdy x = 0, wtedy podstawiając x = 0 mamy:
gdy x = 5, wtedy: ![]() dzielenie nie jest wykonalne czyli ułamek nie ma sensu liczbowego.
dzielenie nie jest wykonalne czyli ułamek nie ma sensu liczbowego.
Dodając lub odejmując jednomiany otrzymamy SUMĘ ALGEBRAICZNĄ.
Dodawane jednomiany nazywamy wyrazami sumy algebraicznej.
W sumach algebraicznych można dodawać lub odejmować tylko WYRAZY PODOBNE tzn. takie, które mają takie same zmienne literowe w tej samej potędze, a różnią się jedynie współczynnikami cyfrowymi. Mówimy wtedy, że dokonaliśmy REDUKCJI WYRAZÓW PODOBNYCH.
Polega ona na tym, że dodajemy lub odejmujemy współczynniki cyfrowe wyrazów, a zmienne literowe zostają bez zmiany.
Sumy algebraiczne można:
- dodawać
- odejmować – otrzymujemy w wyniku sumę algebraiczną
- mnożyć
- dzielić – otrzymujemy ułamek algebraiczny lub sumę algebraiczną
1. Przy dodawaniu sum algebraicznych opuszczamy nawiasy pozostawiając znaki wyrazów dodawanych bez zmiany i wykonujemy redukcję wyrazów podobnych doprowadzając do najprostszej postaci, np.:
2. Przy odejmowaniu sum algebraicznych opuszczamy nawiasy pamiętając o zmianie znaków wyrazów w nawiasie, przed którym stał minus, a dalej redukujemy wyrazy podobne również doprowadzając do najprostszej postaci, np.:
3. Mnożąc sumę algebraiczną przez jednomian mnożymy po kolei każdy wyraz tej sumy przez dany jednomian i redukujemy wyrazy podobne, jeśli to możliwe, np.:
4. Dzieląc sumę algebraiczną przez jednomian wykonujemy dzielenie po kolei każdego wyrazu tej sumy przez dany jednomian i redukujemy wyrazy podobne, jeśli jest to możliwe, np.:
5. Mnożąc sumy algebraiczne przez siebie musimy wymnożyć każdy wyraz jednej sumy przez każdy wyraz drugiej sumy i otrzymane wyrazy zredukować, jeśli jest to możliwe, np.:
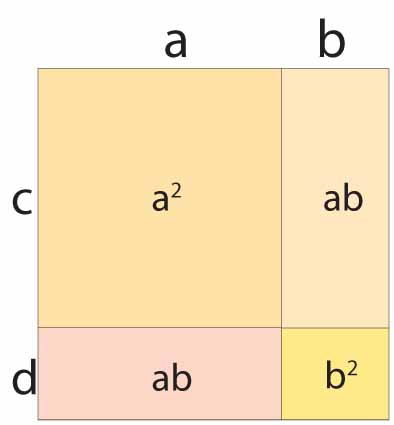
Interpretacja geometryczna tego mnożenia jest następująca:
Lewa strona L, to pole prostokąta, którego długości boków wynoszą
(a + b) i (c + d)
Prawa strona P, to suma pól części składowych tego prostokąta
czyli ac + ad + bc + bd
Przykład:
Szczególnym przypadkiem mnożenia sum algebraicznych jest mnożenie jednakowych czynników, np.: (a + b)(a + b) czyli ![]() . W interpretacji geometrycznej wygląda to tak:
. W interpretacji geometrycznej wygląda to tak:
Pole kwadratu o boku (a + b) czyli ![]() jest równe
jest równe
sumie pól kwadratów ![]() i
i ![]() oraz prostokątów ab i ab, stąd
oraz prostokątów ab i ab, stąd
Jest to wzór należący do wcale niemałej grupy wzorów skróconego mnożenia, które to, jak sama nazwa wskazuje, ułatwiają mnożenie.
Inne wzory z tej rodziny to:
Przykłady:
Ćwiczenie:
Oblicz wartość liczbową wyrażenia:
1. Wykonuję mnożenie sum algebraicznych oraz stosuję wzory skróconego mnożenia.
2. Opuszczam nawiasy w liczniku i stosuję redukcję wyrazów podobnych. Podstawiam wartości liczbowe zmiennych i otrzymuję:
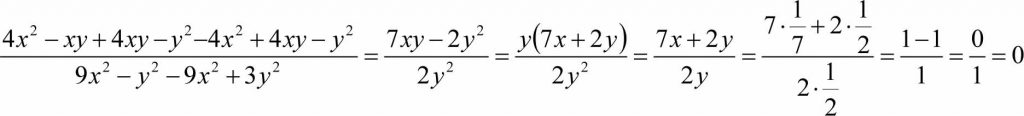 Do działañ na sumach algebraicznych stosuje się te same prawa co do działañ na liczbach rzeczywistych, a mianowicie:
Do działañ na sumach algebraicznych stosuje się te same prawa co do działañ na liczbach rzeczywistych, a mianowicie:
- w dodawaniu – przemienność, łączność;
- w mnożeniu– przemienność, łączność, rozdzielność;
- w dzieleniu– rozdzielność.
Prawo rozdzielności ma również zastosowanie w wyłączaniu czynnika poza nawias. Jest to sposób zamiany sumy algebraicznej na iloczyn (postać iloczynowa jest ważną postacią wyrażenia algebraicznego), np.:
Sumę na iloczyn możemy zamienić stosując również:
Podsumowując, możemy stwierdzić, że zamiana sumy na iloczyn odbywa się poprzez:
- wyłączanie wspólnego czynnika poza nawias,
- stosowanie wzorów skróconego mnożenia,
- grupowanie wyrazów.
Często łączymy te sposoby korzystając z nich równocześnie, np.:
Dział matematyki zajmujący się między innymi wyrażeniami algebraicznymi nazywa się ALGEBRY.