Czworokąt – część płaszczyzny ograniczona łamaną zwyczajną zamkniętą złożoną z czterech odcinków.
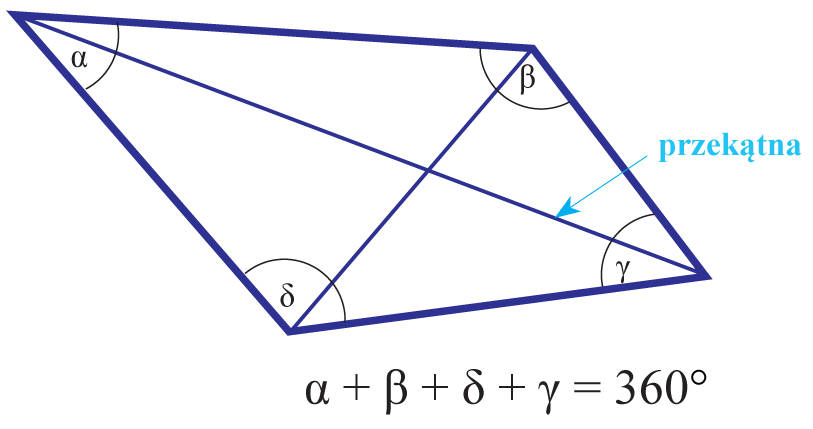
Przekątna wielokąta to odcinek łączący dwa niekolejne wierzchołki wielokąta. W każdym czworokącie można poprowadzić dwie przekątne.
Suma miar kątów wewnętrznych czworokąta wynosi 360°.
Zapamiętaj!
Wzór na sumę kątów dowolnego wielokąta wypukłego to S = (n-2)⋅180° gdzie n oznacza oczywiście liczbę kątów wielokąta.
Wielokąt wypukły to taki, w którym każdy kąt wewnętrzny ma miarę mniejszą niż 180°.
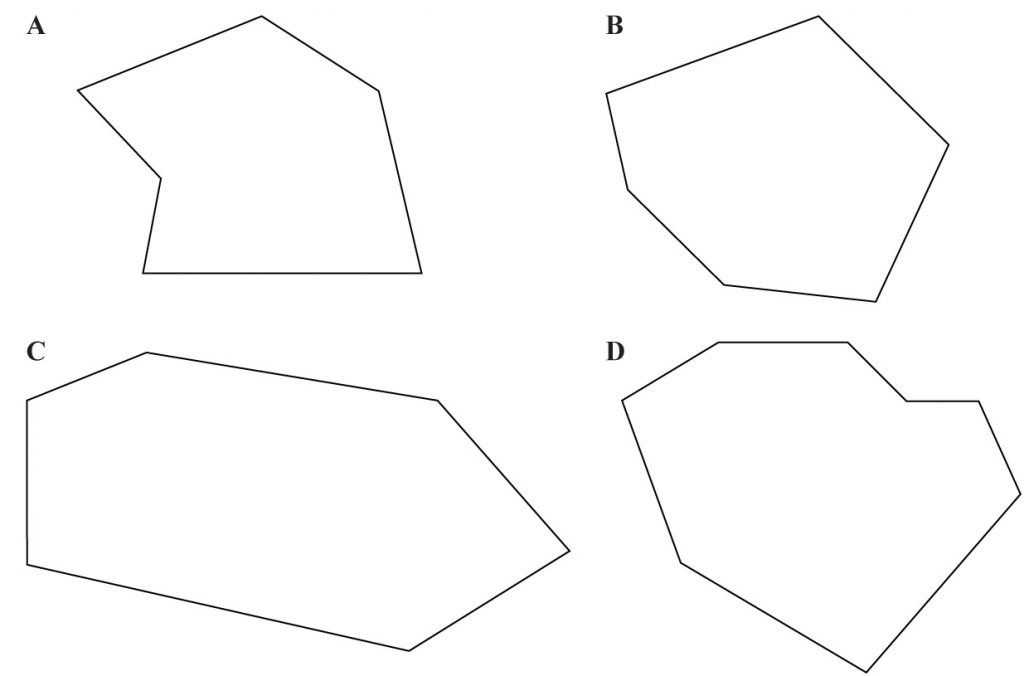
Oto cztery wielokąty. Dwa z nich są wypukłe. Które?
Wielokąty wypukłe to B i C.
Prostokąt, kwadrat
Własności prostokąta:
- wszystkie kąty proste,
- przekątne równej długości,
- przekątne dzielą się na połowy.
Własności kwadratu:
- wszystkie boki równe,
- wszystkie kąty proste.
Przekątne kwadratu są:
- równej długości,
- prostopadłe,
- dzielą się na połowy,
- dwusiecznymi kątów wewnętrznych,
- osiami symetrii.
Koniecznie pamiętaj wzory!
- Pole kwadratu o boku a: P = a²
- Obwód kwadratu o boku a: L = 4a
- Długość przekątnej kwadratu o boku a: d = a √2
- Pole prostokąta o bokach a i b: P = a · b
- Obwód prostokąta o bokach a i b: L = 2a + 2b
Uwaga!
Jeśli obwody dwóch figur są takie same, to nie oznacza to, że ich pola też są równe.
Pole powierzchni figury wskazuje, ile kwadratów jednostkowych zmieści się w danej figurze. Pole wyrażamy w jednostkach kwadratowych oraz w przypadku dużych powierzchni w arach i hektarach.
Pole figury, jeśli istnieje, jest liczbą nieujemną.
Obwód wielokąta to suma długości wszystkich jego boków. Obwody wyrażamy w jednostkach długości.
Zadanie 1.
W prostokącie o polu 32 jeden z boków jest dwa razy dłuższy niż drugi. Obwód tego prostokąta jest równy:
A. 12
B. 16
C. 20
D. 24
Rozwiązanie:
x – długość krótszego boku prostokąta
2x – długość dłuższego boku prostokąta
Stąd x · 2x = 2x² = 32, czyli x² = 16
x = 4
2x = 8
Obliczmy obwód Ob = 2 · 4 + 2 · 8 = 24
Odpowiedź: D.
Zadanie 2.
Na działce wybudowano dom o podstawie w kształcie kwadratu o przekątnej 11√2 m i garaż o podstawie prostokąta o bokach 30 dm i 8 m. Pozostała część działki o powierzchni 4,78 a jest niezabudowana. Oblicz pole powierzchni działki.
Rozwiązanie:
Kolejno należy obliczyć pola powierzchni domu, garażu, a na końcu całej działki.
Skoro przekątna kwadratu d = 11√2 m, więc bok domu ma
11 m.
Pdomu = 11 · 11 = 121 [m²]
P garażu = 3 · 8 = 24 [m²]
4,78 ara = 478 m²
P działki = 478 + 121 + 24 = 623 [m2] = 6,23 [a]
Odpowiedź: Powierzchnia działki wynosi 6,23 ara.
Zadanie 3.
Dwie prostokątne grządki warzywne mają równe pola. Jedna z nich ma wymiary 5 m i 4,2 m. Jaką długość ma druga grządka, jeżeli jej szerokość wynosi 3 m?
A. 62 cm
B. 70 cm
C. 620 cm
D. 700 cm
Rozwiązanie:
Najpierw obliczamy pole jednej grządki
P = 5 m · 4,2 m = 21 m².
Ponieważ druga grządka ma identyczne pole, zatem po wykonaniu dzielenia otrzymujemy
21 m² : 3 m = 7 m = 700 cm
Odpowiedź: D.
Zadanie 4.
Jaś i Staś postanowili wymienić wykładziny w swoich pokojach, a następnie zabezpieczyć je listwami. Okazało się, że każdy z nich musiał zakupić tyle samo metrów bieżących listwy. Jaś stwierdził, że skoro obwody ich pokojów są równe, to i pole powierzchni wykładziny będzie takie samo. Staś miał odmienne zdanie. Który z nich miał rację, jeżeli wiadomo, że pokój Jasia ma kształt prostokąta o bokach 5 m i 6 m, a pokój Stasia jest kwadratem?
Rozwiązanie:
Najpierw musimy obliczyć obwód pokoju Jasia
Ob = 2 · 5 + 2 · 6 = 22 [m].
Ponieważ Jaś i Staś kupili tyle samo metrów listwy, czyli obwód pokoju Stasia wynosi także 22 m.
Obwód kwadratu 4a = 22 m, a to znaczy, że a = 5,5 m.
Pole pokoju Stasia jest równe 5,5 m · 5,5 m = 30,25 m².
Pole pokoju Jasia wynosi 5 m · 6 m = 30 m².
Odpowiedź: Pola powierzchni wykładzin są różne, zatem rację miał Staś.
Zadanie 5.
Wieża Eiffla znajduje się na obszarze w kształcie kwadratu o boku długości 125 m. Ile hektarów powierzchni ma ten obszar? Zapisz obliczenia. Wynik podaj z dokładnością do 0,1 ha.
Rozwiązanie:
Zwróćcie uwagę, że w tym zadaniu wystarczy znać wzór na pole kwadratu i, oczywiście, pamiętać o zamianie jednostek. Pole kwadratu wynosi: P = 125 m · 125 m = 15 625 m² = = 1,5625 ha » 1,6 ha
Odpowiedź: Powierzchnia obszaru z dokładnością do 0,1 ha wynosi 1,6 ha.
Zadanie 6.
Wokół znajdującej się w parku prostokątnej rabaty kwiatowej o wymiarach 3 m x 5 m poprowadzono ścieżkę o szerokości 0,9 m. Jakie pole powierzchni ma ta ścieżka?
Rozwiązanie:
W takim zadaniu warto sporządzić pomocniczy rysunek, który zobrazuje sytuację opisaną w zadaniu:
Skoro ścieżka ma szerokość 0,9 m, to wymiary rabaty ze ścieżką wynoszą 6,8 m x 4,8 m. Chcąc wyliczyć pole ścieżki, wystarczy od pola dużego prostokąta odjąć pole małego prostokąta:
Pścieżki = Pdużego – Pmałego
Pścieżki = 6,8 m · 4,8 m – 5 m · 3 m = 32,64 m² – 15 m² = 17,64 m²
Odpowiedź: Ścieżka ma powierzchnię 17,64 m².
Uwaga! Pole ścieżki można wyliczyć innymi sposobami!
Zadanie 7
Boisko szkolne jest czworokątem o bokach: 139 m, 111 m, 125 m i 116 m. Zostało ono ogrodzone siatką. W ogrodzenie wmontowano dwie stalowe bramy, każda o szerokości 3 metrów. Ile metrów bieżących siatki zużyto na wykonanie ogrodzenia boiska?
A. 497 m
B. 491 m
C. 488 m
D. 485 m
Powtórz!
Jednostki długości:
1 cm = 10 mm
1 dm = 10 cm = 100 mm
1 m = 10 dm = 100 cm = 1000 mm
1 km = 1000 m
Rozwiązanie:
Ilość siatki potrzebnej do ogrodzenia działki wyliczysz, wykonując działanie:
139 m + 111 m + 125 m + 116 m – 2 · 3 m = = 485 m
Odpowiedź: D.
Zadanie 8
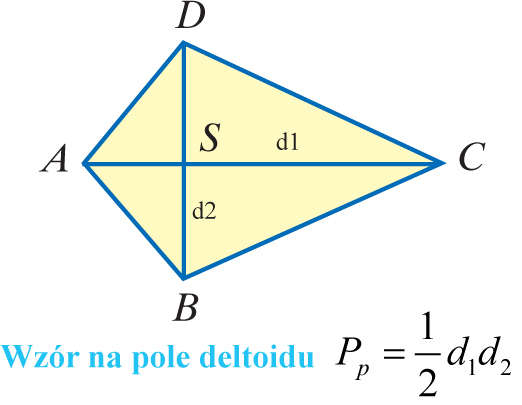
Przed przystąpieniem do budowy latawca Janek rysuje jego model. Model ten przedstawiono na rysunku w skali 1:10. Oblicz pole powierzchni latawca zbudowanego przez Janka, wiedząc, że długości odcinków AC i BD równe są odpowiednio 4 cm i 2 cm oraz AC ⊥ BD i S – środek BD. Zapisz obliczenia.
Powtórz!
Deltoid to czworokąt, w którym:
- dwie pary boków są równe,
- przekątne są prostopadłe,
- jedna z przekątnych dzieli drugą na połowy.
Rozwiązanie:
Rzeczywiste wymiary przekątnych wynoszą:
4 cm · 10 = 40 cm, 2 cm · 10 = 20 cm. (ponieważ rysunek został wykonany w skali)
Pole powierzchni latawca, który ma kształt deltoidu, wynosi:
P = · 40 cm · 20 cm = 400 cm²
Zadanie 9
Wydzielona przy szkole część parku zajmuje powierzchnię 175 m². Ile to km²?
A. 0,000175
B. 0,00175
C. 0,0175
D. 0,175
Odpowiedź: A.
Zadanie 10
Wieża Eiffla znajduje się na obszarze w kształcie kwadratu o boku długości 125 m.
Ile hektarów powierzchni ma ten obszar? Zapisz obliczenia. Wynik podaj z dokładnością do 0,1 ha.
Pamiętaj!
Gdy zaokrąglamy do części dziesiątych, o wyniku zaokrąglenia decyduje cyfra części setnych. Jeśli cyfra części setnych jest równa 5 lub jest większa od 5, to zaokrąglamy w górę. Jeśli cyfra części setnych jest mniejsza od 5, to zaokrąglamy w dół.
Gdy zaokrąglamy do dziesiątek, o wyniku zaokrąglenia decyduje cyfra jedności, gdy zaokrąglamy do setek – decyduje cyfra dziesiątek itd.
Rozwiązanie:
Pole kwadratu wynosi 125 m · 125 m = = 15 625 m² » 1,6 ha.
Poćwicz
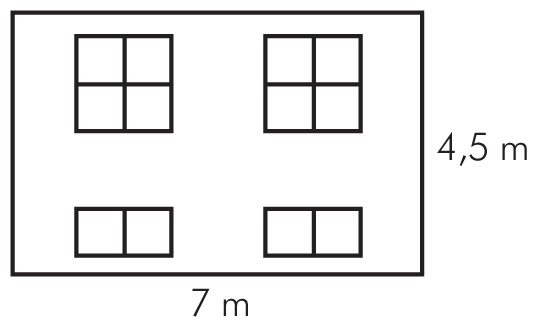
1) Ile metrów kwadratowych styropianu potrzeba na ocieplenie ściany domu o wymiarach podanych na rysunku, jeżeli na ścianie tej znajdują się dwa okna w kształcie kwadratu o boku 1,5 m i dwa okna o powierzchni dwa razy mniejszej?
A. 27 m²
B. 24,75 m²
C. 31,5 m²
D. 29,25 m²
2) Prostokątny plac zabaw o obwodzie 162 m ma szerokość dwa razy mniejszą od długości. Pole powierzchni placu wynosi:
A. 54 m²
B. 1458 m²
C. 5832 m2²
D. 3445 m²
3) Stolarz otrzymał zamówienie na wykonanie blatu stołu w kształcie kwadratu o obwodzie 48 dm. Pole powierzchni tego blatu wynosi:
A. 1,44 m²
B. 14,4 m²
C. 23,04 m²
D. 1,2 m²
4) Z obrusu w kształcie koła o średnicy 1,6 m wykonano kwadratową serwetę o przekątnej równej średnicy koła. Powstałą serwetę obszyto ozdobną taśmą. Ile metrów taśmy zużyto?
A. 6,4 m
B. 0,8√2 m
C. 3,2√2 m
D. 1,28 m
5) Ile osi symetrii ma figura przedstawiona na rysunku?
A. Nieskończenie wiele.
B. Żadnej.
C. Dwie.
D. Cztery.
Rozwiązania:
1. B, 2. B, 3. A, 4. C, 5. D
1. Który z czworokątów o podanych miarach dwóch kątów jest równoległobokiem:
A. 20°, 80°
B. 75°, 115°
C. 140°, 60°
D. 90°, 90°
2. W trójkącie równoramiennym dwa boki mają długości 4 cm i 9 cm. Jaką długość ma trzeci bok?
A. 4 cm
B. 5 cm
C. 9 cm
D. Dowolną długość.
3. Wokół kwiatowej rabaty w kształcie kwadratu o obwodzie 20 m poprowadzono ścieżkę o szerokości 70 cm. Pole powierzchni tej ścieżki wynosi:
A. 25 m²
B. 25,6 m²
C. 15,96 m²
D. 28,49 m²
4. Gdy ustawimy pola powierzchni:
p = 4 ha
r = 0,06 km²
s = 3 000 000 dm²
t = 500 a
w kolejności od najmniejszej do największej, otrzymamy układ liter:
A. s, p, t, r
B. p, t, r, s
C. r, p, t, s
D. s, t, r, p
5. Prostokątny plac zabaw o polu 162 m2 ma szerokość dwa razy mniejszą od długości. Obwód placu wynosi:
A. 1458 m
B. 162 m
C. 54 m
D. 27 m
Odpowiedzi:
1. D, 2. C, 3. C, 4. A, 5.
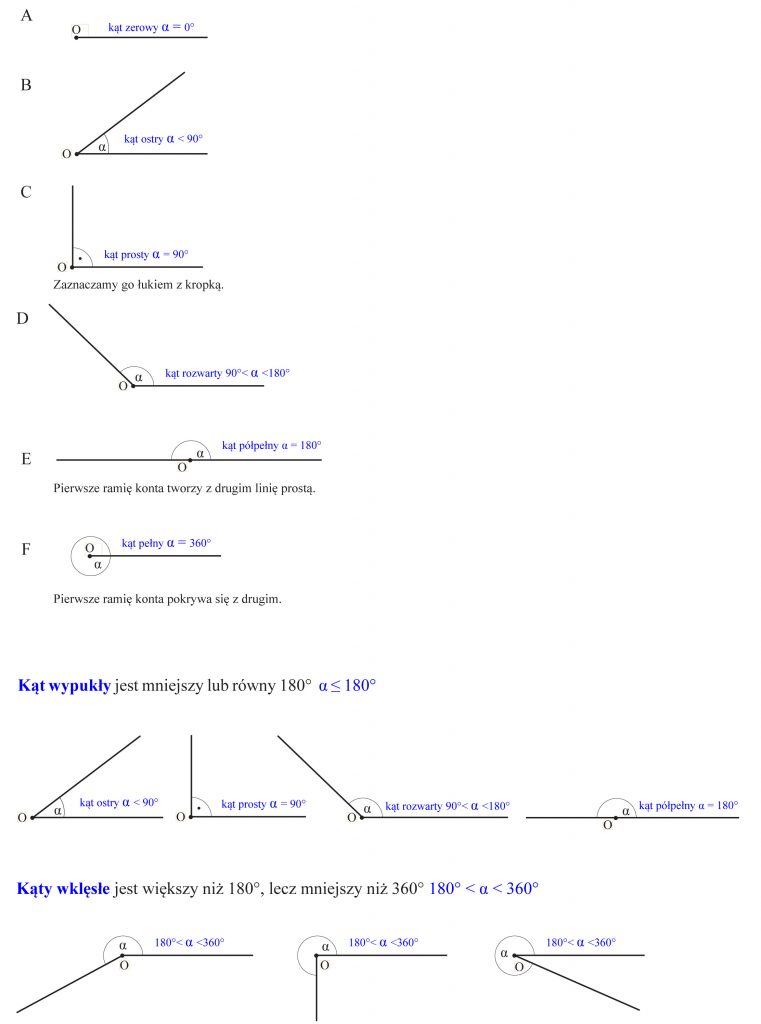
To koniecznie powtórz przed egzaminem!
Rodzaje kątów: